Abstract

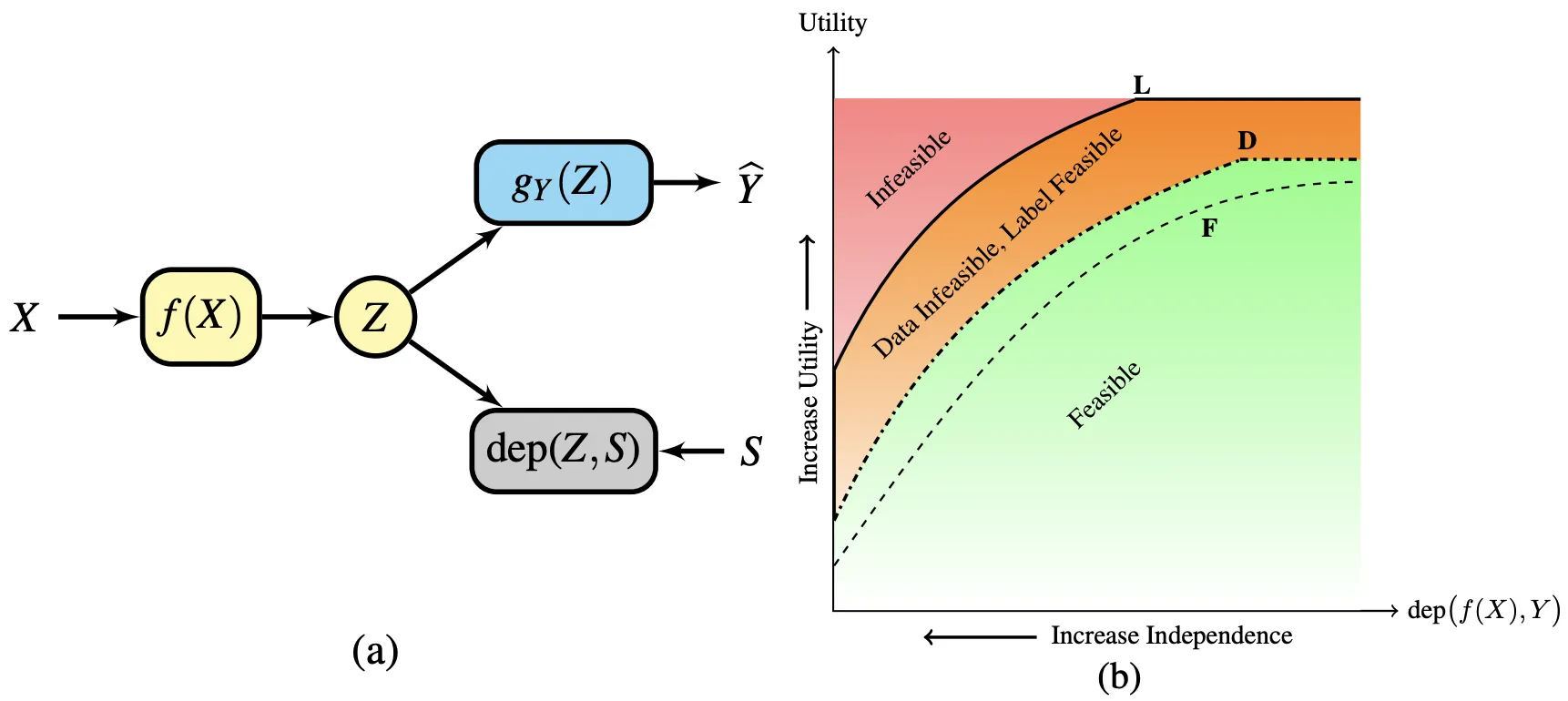
Many applications of representation learning, such as privacy preservation, algorithmic fairness, and domain adaptation, desire explicit control over semantic information being discarded. This goal is formulated as satisfying two objectives: maximizing utility for predicting a target attribute while simultaneously being invariant (independent) to a known semantic attribute. Solutions to invariant representation learning (IRepL) problems lead to a trade-off between utility and invariance when they are competing. While existing works study bounds on this trade-off, two questions remain outstanding: 1) What is the exact trade-off between utility and invariance? and 2) What are the encoders (mapping the data to a representation) that achieve the trade-off, and how can we estimate it from training data? This paper addresses these questions for IRepLs in reproducing kernel Hilbert spaces (RKHS)s. Under the assumption that the distribution of a low-dimensional projection of high-dimensional data is approximately normal, we derive a closed-form solution for the global optima of the underlying optimization problem for encoders in RKHSs. This in turn yields closed formulae for a near-optimal trade-off, corresponding optimal representation dimensionality, and the corresponding encoder(s). We also numerically quantify the trade-off on representative problems and compare them to those achieved by baseline IRepL algorithms.