Abstract

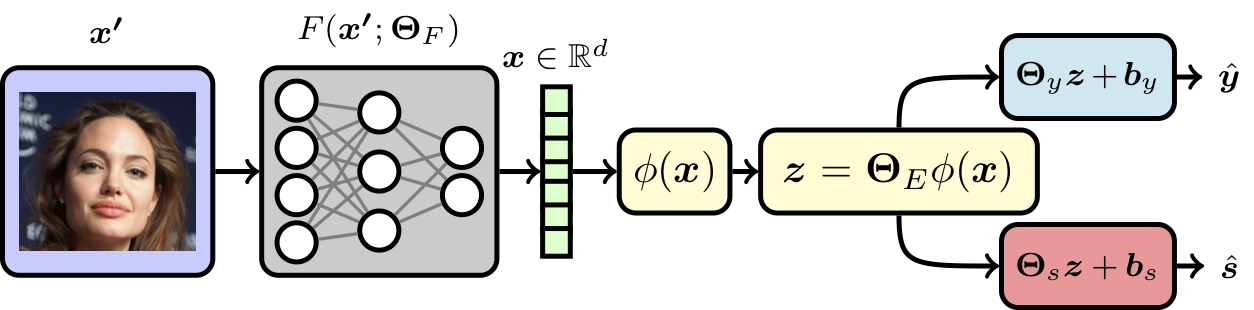
Adversarial representation learning is a promising paradigm for obtaining data representations that are invariant to certain sensitive attributes while retaining the information necessary for predicting target attributes. Existing approaches solve this problem through iterative adversarial minimax optimization and lack theoretical guarantees. In this paper, we first study the “linear” form of this problem i.e., the setting where all the players are linear functions. We show that the resulting optimization problem is both non-convex and non-differentiable. We obtain an exact closed-form expression for its global optima through spectral learning and provide performance guarantees in terms of analytical bounds on the achievable utility and invariance. We then extend this solution and analysis to non-linear functions through kernel representation. Numerical experiments on UCI, Extended Yale B and CIFAR-100 datasets indicate that, (a) practically, our solution is ideal for “imparting” provable invariance to any biased pre-trained data representation, and (b) empirically, the trade-off between utility and invariance provided by our solution is comparable to iterative minimax optimization of existing deep neural network based approaches.

Poster