Abstract

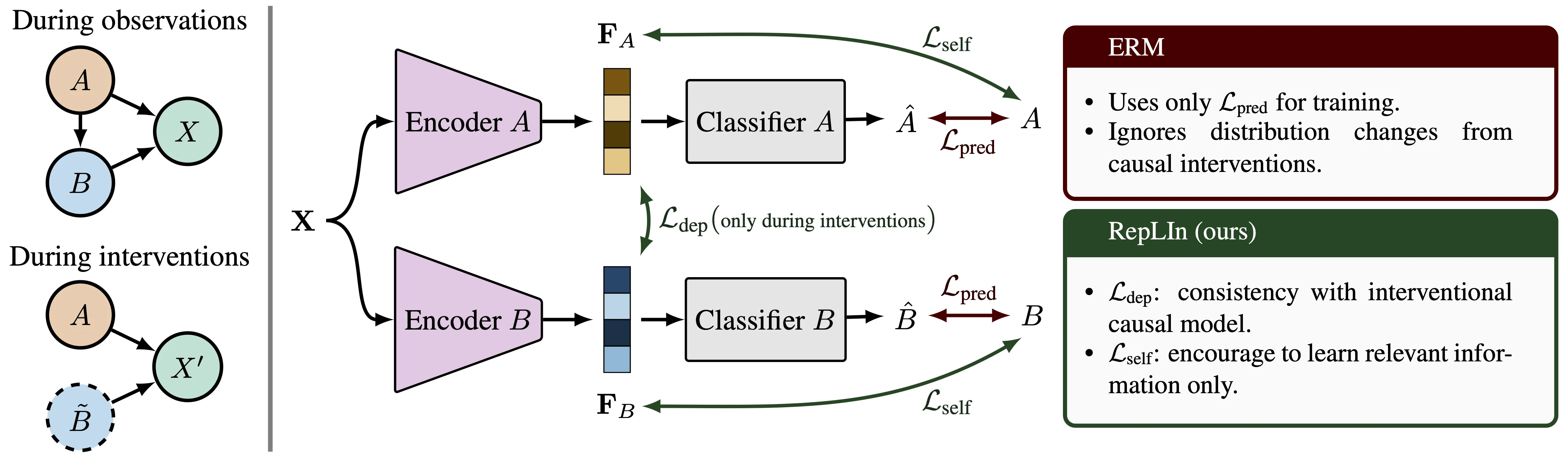
We consider the problem of learning robust discriminative representations of latent variables that are causally related to each other via a directed graph. In addition to passively collected observational data, the training dataset also includes interventional data obtained through targeted interventions on some of these latent variables to learn representations that are robust against the resulting interventional distribution shifts. However, existing approaches treat interventional data like observational data, even when the underlying causal model is known, and ignore the independence relations that arise from these interventions. Since these approaches do not fully exploit the causal relational information resulting from interventions, they learn representations that produce large disparities in predictive performance on observational and interventional data. This performance disparity worsens when the number of interventional data samples available for training is limited. In this paper, (1) we first identify a strong correlation between this performance disparity and adherence of the representations to the statistical independence conditions induced by the underlying causal model during interventions. (2) For linear models, we derive sufficient conditions on the proportion of interventional data in the training dataset, for which enforcing statistical independence between representations corresponding to the intervened node and its non-descendants during interventions lowers the test-time error on interventional data. Combining these insights, (3) we propose RepLIn, a training algorithm to explicitly enforce this statistical independence during interventions. We demonstrate the utility of RepLIn on a synthetic dataset and on real image and text datasets on facial attribute classification and toxicity detection, respectively, with semi-synthetic causal structures. Our experiments show that RepLIn is scalable with the number of nodes in the causal graph and is suitable to improve the robustness of representations against interventional distribution shifts of both continuous and discrete latent variables compared to the ERM baselines.