The Art of Unseeing Ghosts in our Data


UCR RAISE Seminar Series

Slides: hal.cse.msu.edu/talks
VishnuBoddeti

Michigan State University


Proliferation of AI in Our Lives

Tesla FSD
Chat Bots
Rapid AI
Walker from UBTECH

At the core of these AI systems are...

If the inference query was not observed during training...

    • Spurious correlation: Using by-chance correlated features for prediction.
    • Stereotypes and bias: Assuming social stereotypes to aid prediction.
    • Hallucination: Conjuring up premises and relations to provide human-friendly output.

What are the Consequences?

State-of-Affairs
(report from the real-world)
Facial recognition bias frustrates Black asylum applicants to US, advocates say


"How AI reduces the world to stereotypes"
"LLMs propagate race-based medicine"
Real world machine learning systems are effective but,


are biased,


are brittle w.r.t distributional shifts and


not trustworthy enough.

Modeling Approach: Pearls' Causal Hierarchy




Key Idea: interventions induce (conditional) independence relations

Today's Agenda



Heat-Assisted Detection and Ranging

(Nature, 2023)



Mitigating Spurious Correlations in Generative Models

(Gaudi et al. ICLR '25, Dehdashtian et al. ICLR '25, NeurIPS '25)



Heat-Assisted Detection and Ranging

(Nature, 2023)

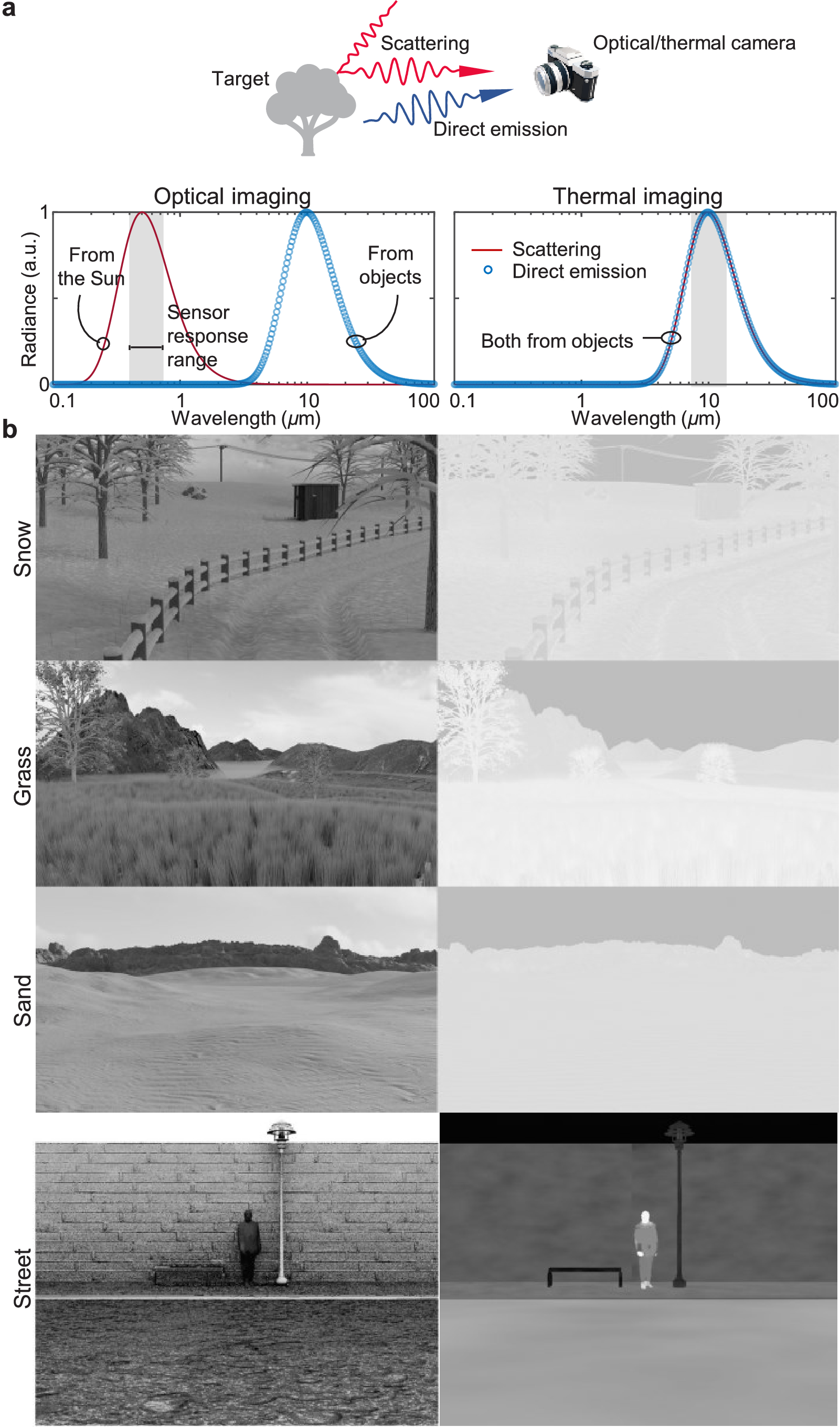
"Ghosting Effect" in Thermal Vision




Why are thermal images blurry?



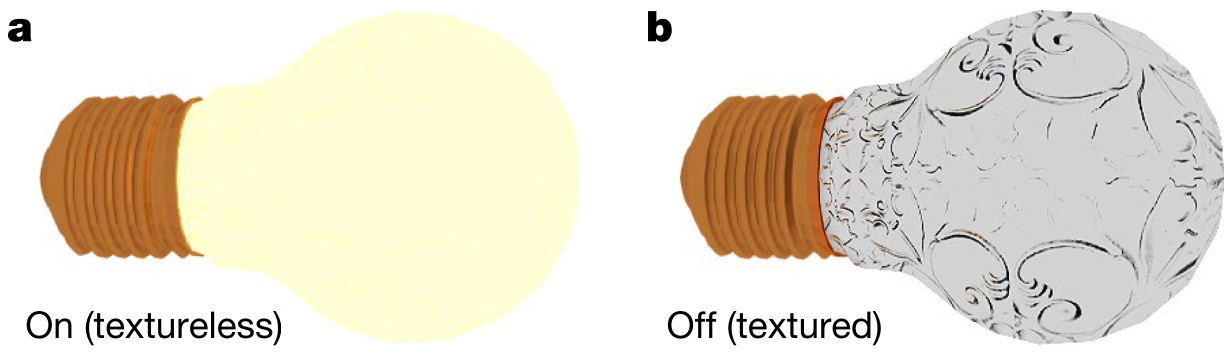
Ghosting effect: when radiated signal is stronger than reflected ambient signal.

TeX decomposition of thermal signals

Observed: $R(\lambda) = (1-e(\lambda))X+e(\lambda)B_{\lambda}(T)$

Challenges in Learning TeX Decomposition

    • Identifiability: Two objects with different T and e may end up giving the same heat signal.
    • Number of objects in the scene: Hard to estimate.
    • Possible Materials: Open-ended. We approximate emissivity as linear subspace of known material emissivities.

TeX Decomposition of Thermal Signals

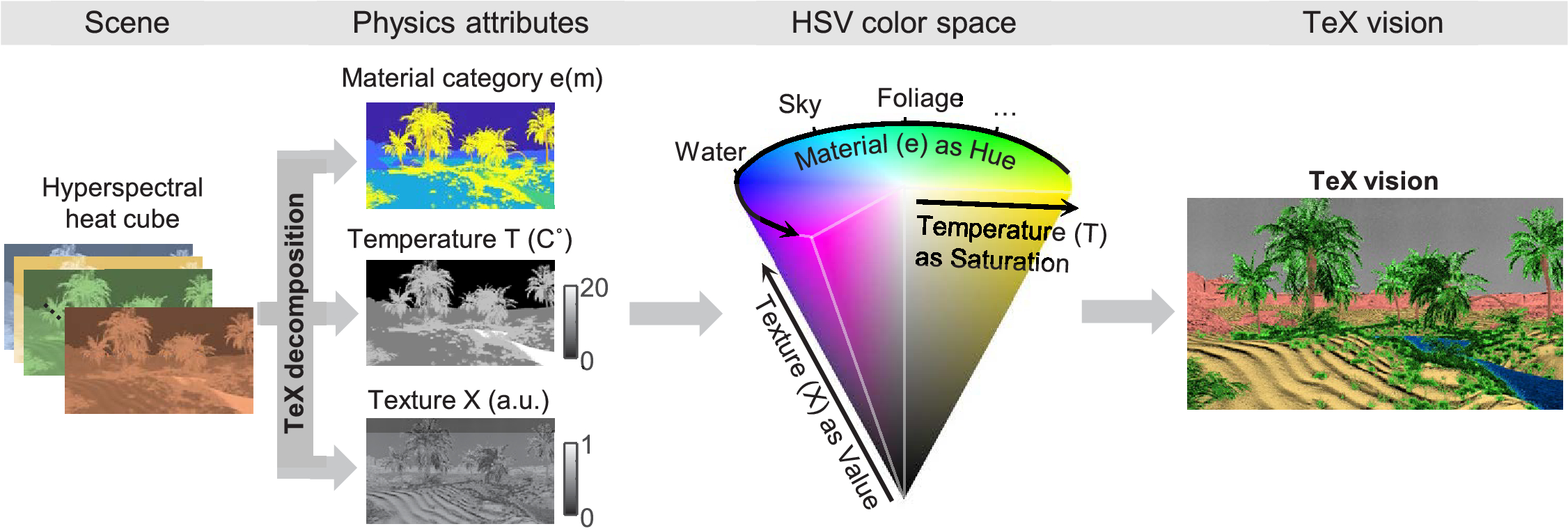
  • TeX Decomposition: Solve inverse problem with custom regularization
    • $${T, e(\lambda), X} = \argmin_{T, e(\lambda), X} \left\| R(\lambda) - (1-e(\lambda))X - e(\lambda) B_{\lambda}(T) \right\|_2 + \phi(T, e(\lambda), X)$$

Thermal vs TeX Decomposition

Heat Assisted Detection

Heat Assisted Ranging

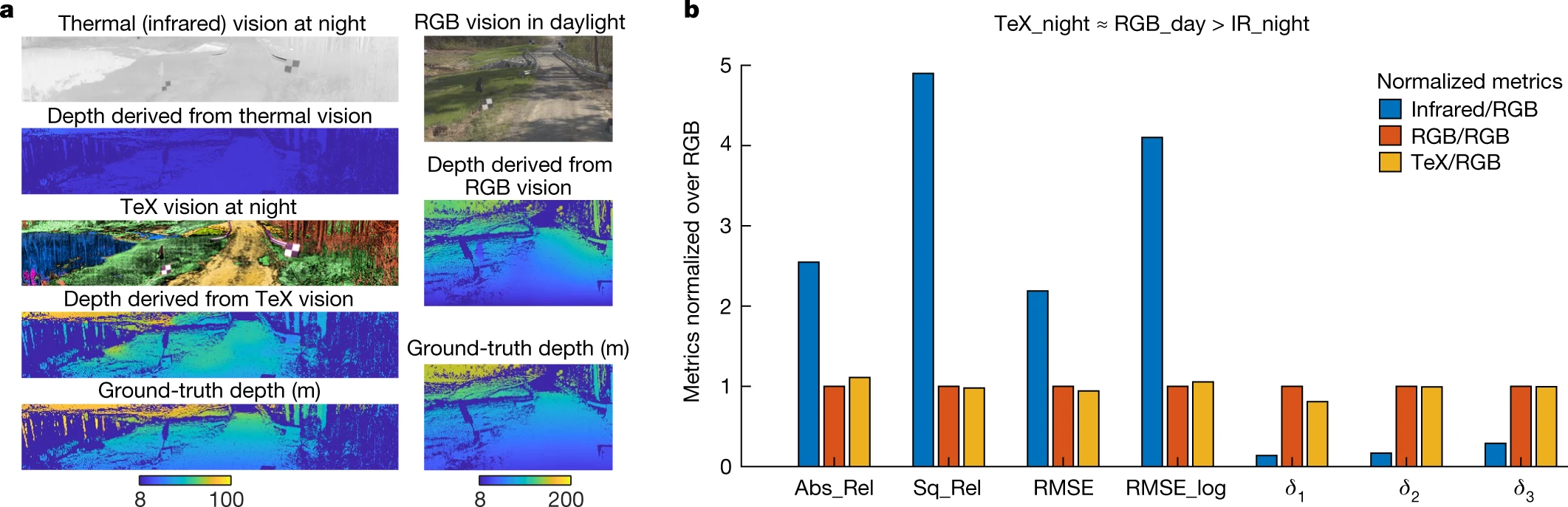
$TeX_{night} \approx RGB_{day} > IR_{night}$


Mitigating Bias in Discriminative Models

(CVPR '19, ICCV '19, TMLR '22, ICLR '24, CVPR '24, NeurIPS '25)

An Anti-Causal Perspective

Observational Causal Graph
Intervention is achieved through conditional independence ($\hat{Y} \perp \!\!\! \perp S$).

Statistical Dependence Formulation

  • Bi-Objective Optimization Problem:
    • Encoder extracts features $\mathbf{z}$
    • Statistical dependence between target task and features $\mathbf{z}$
    • Statistical dependence between sensitive attribute and features $\mathbf{z}$
    $$ \begin{equation} \begin{aligned} \max_{\mathbf{\Theta}_E} & \text{ } \underbrace{\color{cyan}{Dep(Z,Y)}}_{\color{cyan}{\text{target dependence}}} \quad s.t. \text{ } \underbrace{\color{orange}{Dep(Z,S)}}_{\color{orange}{\text{sensitive dependence}}} \leq \alpha \nonumber \end{aligned} \end{equation} $$

Many Solutions for Bias Mitigation

    • Standard Adversarial Representation Learning
    • Linear Adversarial Measure: linear dependency between $Z$ and $S$ [ICCV 2019, CVPRW 2020]
    • Non-Linear Adversarial Measure: Beyond linear dependency between $Z$ and $S$, but not all types [ECML 2021]
    • Universal Dependence Measure: All types of dependency between $Z$ and $S$ [TMLR 2022]
    • End-to-End Universal Dependence Measure: All types of dependency between $Z$ and $S$ [CVPR 2024]

Utility-Fairness Trade-Offs

CelebA
  • Sadeghi, Dehdashtian, Boddeti, "On Characterizing the Trade-off in Invariant Representation Learning," TMLR 2022
  • Dehdashtian, Sadeghi, Boddeti, "Utility-Fairness Trade-Offs and How to Find Them," CVPR 2024

Bias in CLIP's Zero-Shot Prediction

Error: Unable to load Plotly figure.
  • Dehdashtian*, Wang* and Boddeti, "FairerCLIP: Debiasing CLIP's Zero-Shot Predictions using Functions in RKHSs," (ICLR 2024)

Debiasing CLIP Models

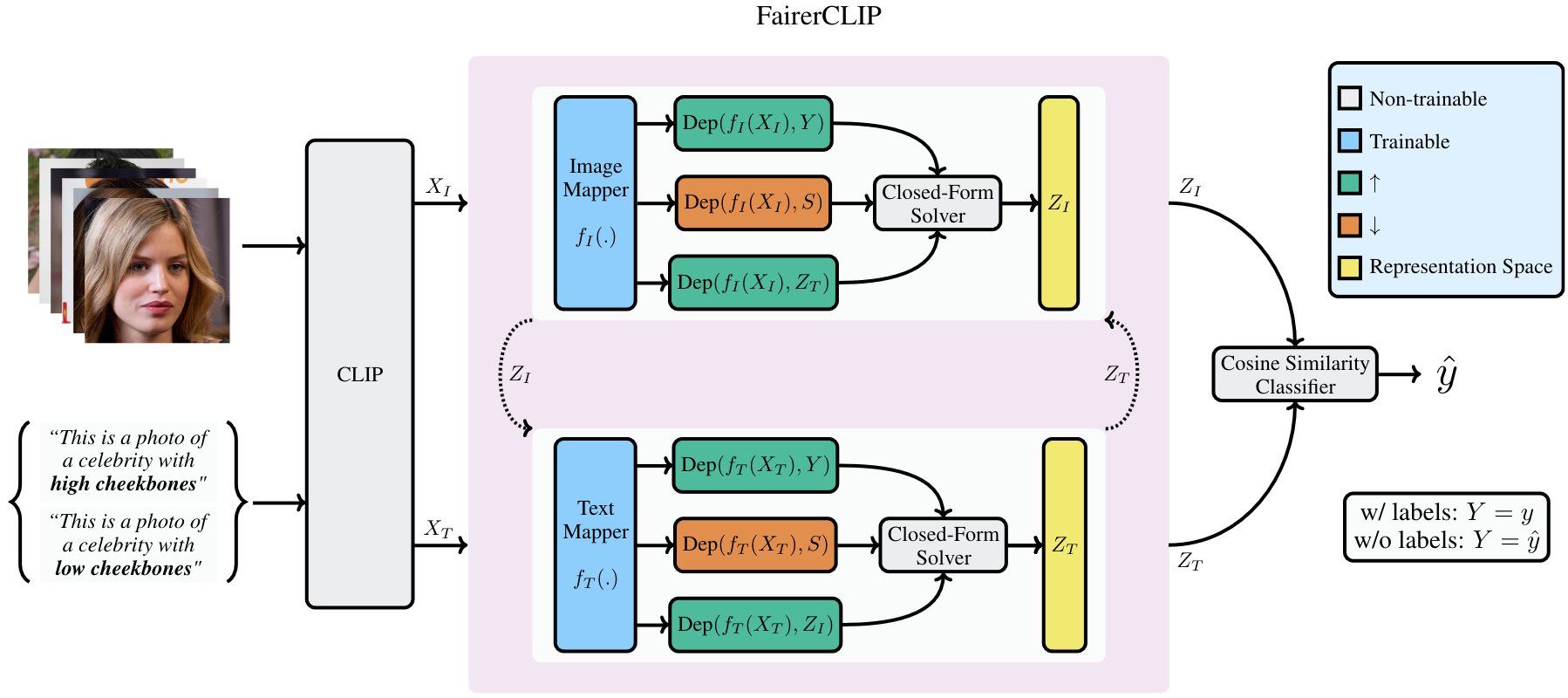
  • Dehdashtian*, Wang* and Boddeti, "FairerCLIP: Debiasing CLIP's Zero-Shot Predictions using Functions in RKHSs," (ICLR 2024)

Debiasing CLIP Models

Error: Unable to load Plotly figure.

  • Dehdashtian*, Wang* and Boddeti, "FairerCLIP: Debiasing CLIP's Zero-Shot Predictions using Functions in RKHSs," (ICLR 2024)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)
  • Akbari*, Afshari* and Boddeti, "Obliviator Reveals the Cost of Nonlinear Guardedness in Concept Erasure," (NeurIPS 2025)


Mitigating Spurious Correlations in Generative Models

(Gaudi et al. ICLR '25, Dehdashtian et al. ICLR '25, NeurIPS '25)

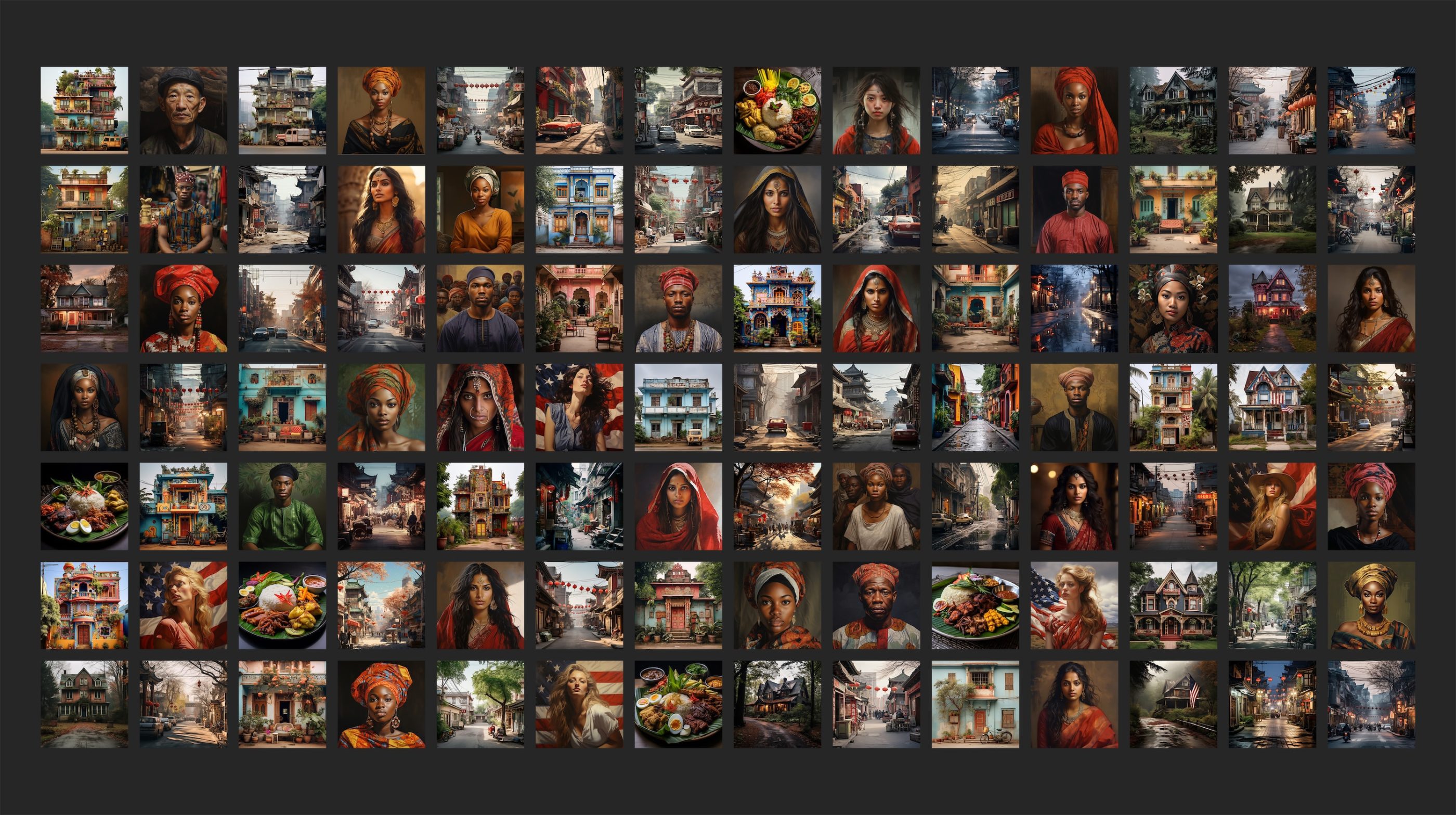
Spurious Correlations in Generative Models


Non-uniform and partial support distributions

High-Quality T2I Models, Same Old Stereotypes

OASIS: Toolbox for Measuring and Understanding Stereotypes

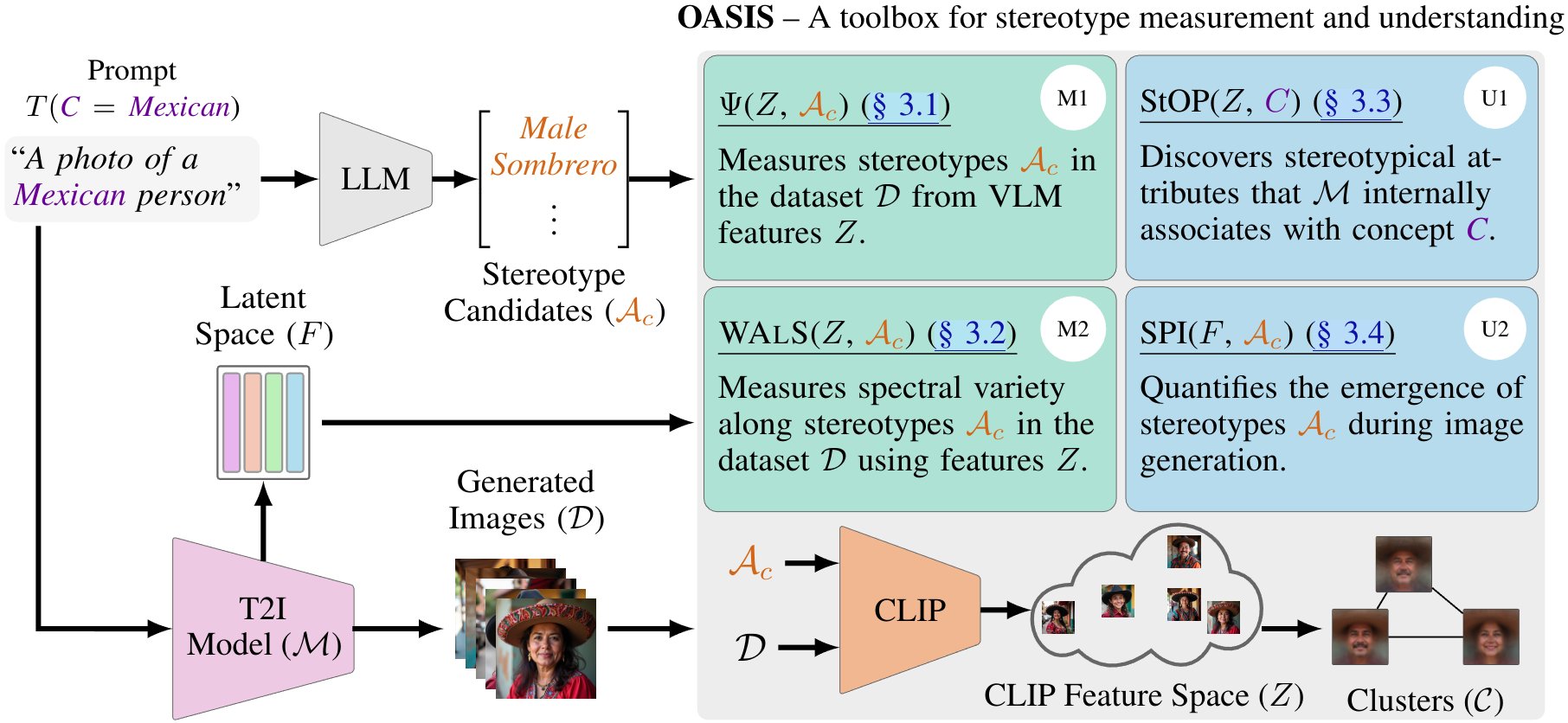
Lower, Yet Significant Stereotypes in Newer T2I Models

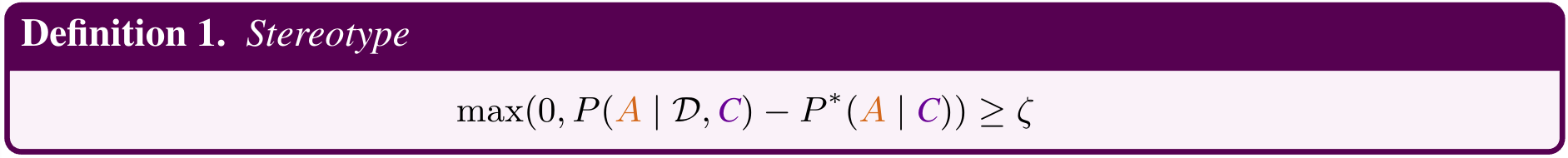
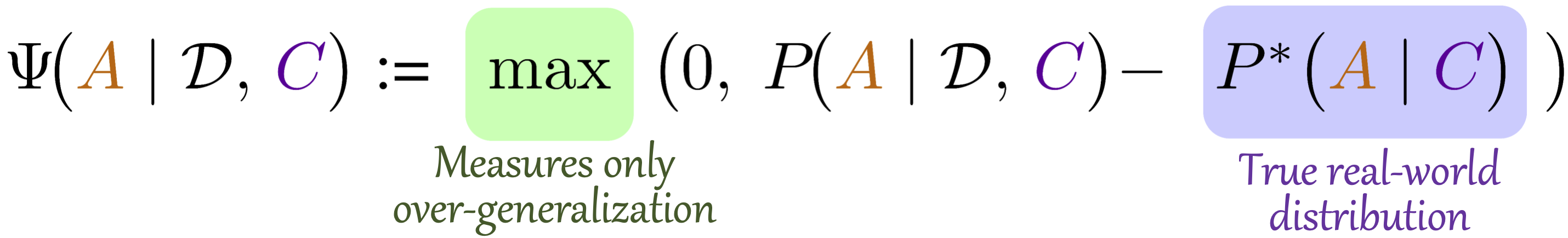
T2I Models Have Stereotypical Predispositions about Nationalities

Indian

Breaking the Spurious Correlations During Sampling

Consider multiple particles: $Z=[z_1, z_2, ..., z_n]$



  • Natural Trajectory: $$dz_i = v_{\theta}(z_i)dt$$




  • Intervened Trajectories: $$dz_i = \underbrace{v_{\theta}(z_i)dt}_{\text{Attractive Force}} + \underbrace{\nabla_{z_i}\det(\Kappa(Z))}_{\text{Repulsive Force}}$$

Mitigating Stereotypes During Sampling

Counterfactual Steering of T2I Models

Steering T2I Models to Red-Team Synthetic Image Detectors

Stereotypes worsen with compositional concepts

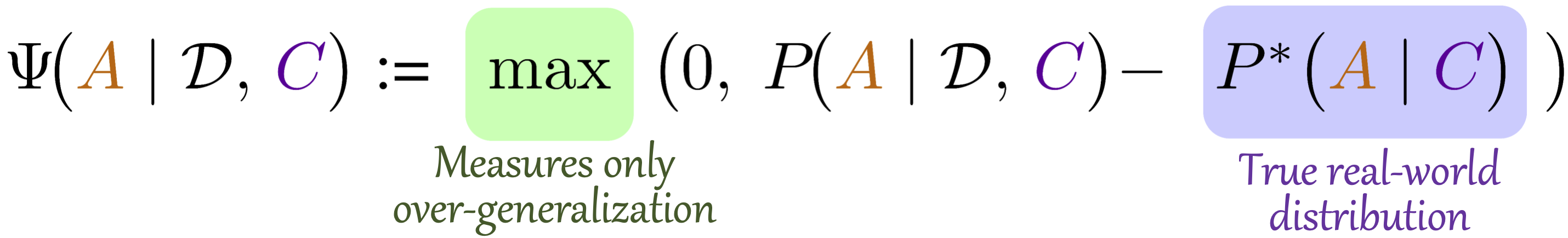
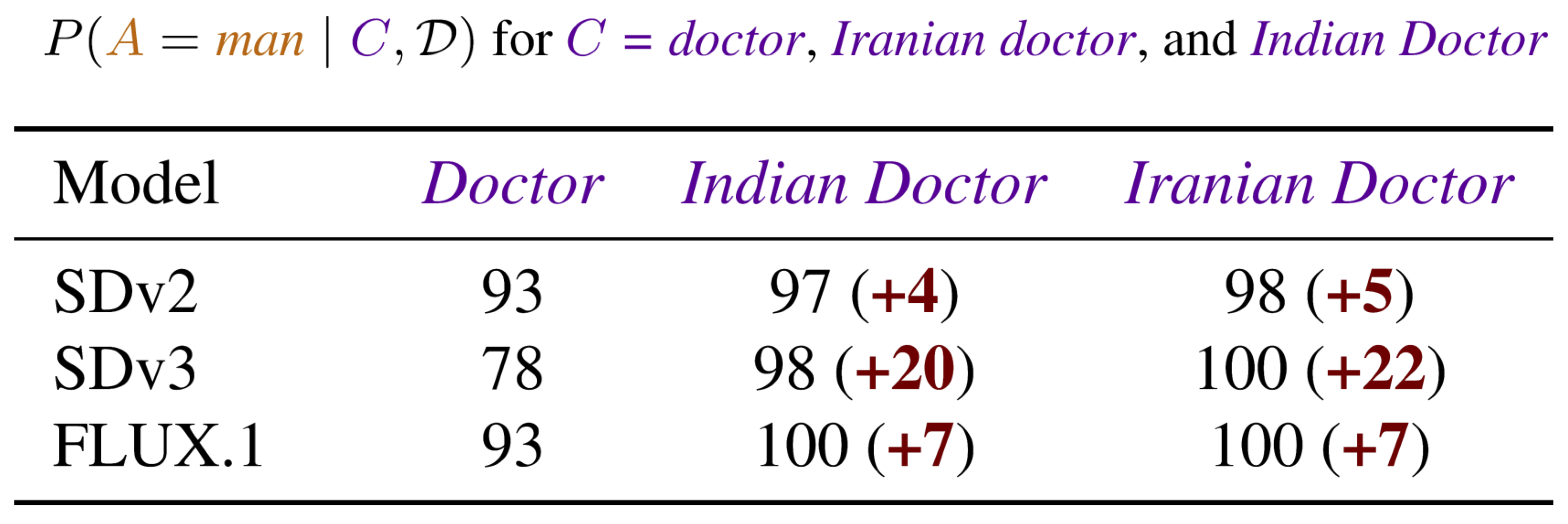
Nationality worsens existing gender stereotypes about professions.

Learning to Mitigate Spurious Correlations

$$\mathcal{L}_{score} = \mathbb{E}_{p({\bm{X},C})}\lVert \nabla_{\bm{X}} \log p_{\bm{\theta}}(\bm{X} \mid C) - \nabla_{\bm{X}}\log p(\bm{X} \mid C)\rVert_2^2$$ $$\mathcal{L}_{CI} = \mathbb{E}_{p(\bm{X},C)}\mathbb{E}_{j,k}\lVert\nabla_{\bm{X}} \log p_\theta(\bm{X}\mid C_j,C_k) - \nabla_{\bm{X}}\log p_\theta(\bm{X} \mid C_j) - \nabla_{\bm{X}}\log p_\theta(\bm{X} \mid C_k)+\nabla_{\bm{X}} \log p_\theta(\bm{X})\rVert_2^2$$ $$\mathcal{L} = \mathcal{L}_{score} + \mathcal{L}_{CI}$$

Generative Models for Robotic Problems

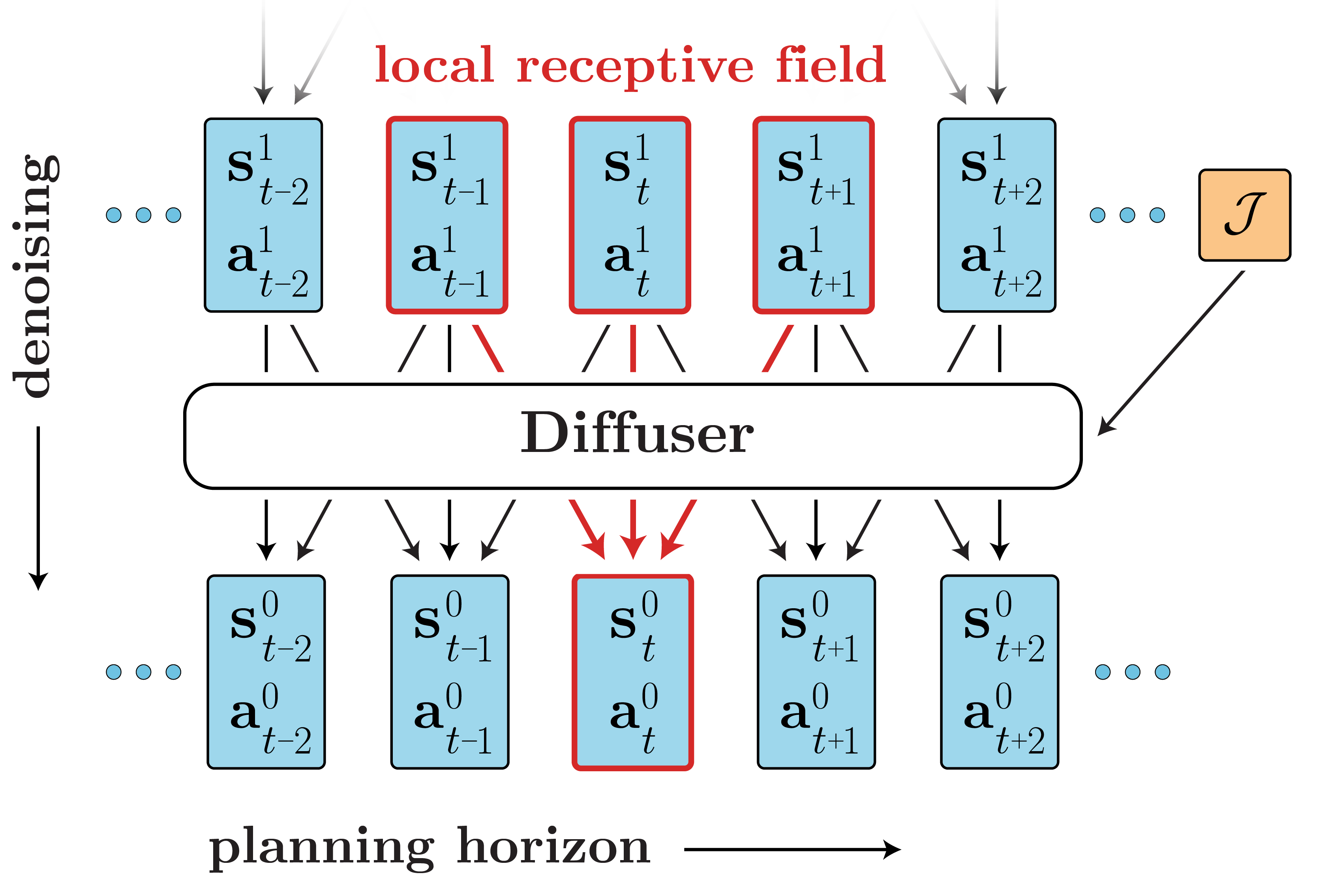
Trajectories for Robotic Arm Manipulation



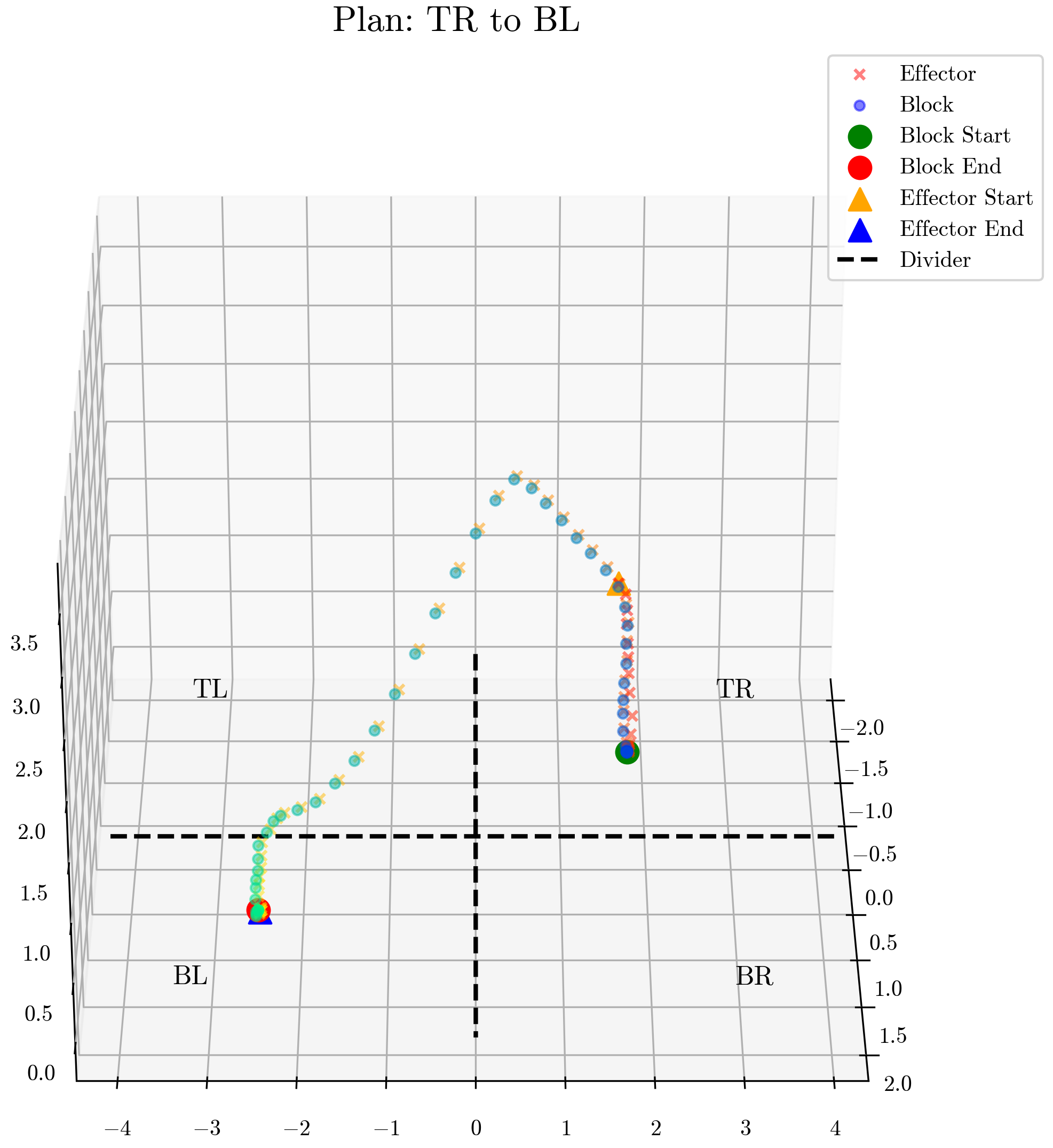
Compositional Generalization for Path Planning

Compositional Generalization for Image Generation

Concluding Remarks

Summary

    • AI systems are progressing at a rapid pace.
      • But, they are still not robust to distributional shifts.

    • A causal perspective is effective for acheiving robustness.

    • Key ideas:
      • Causal modeling of the underlying process.
      • Enforce causal interventions through statistical independence constraints.
      • Effective across multiple applications.

Thank You