Co-Designing AI and Homomorphic Architectures for Secure AI
Pixel Biometrics Seminar
Michigan State University
Progress In Artificial Intelligence
Speech Processing
Image Analysis
Natural Language Processing
Physical Sciences
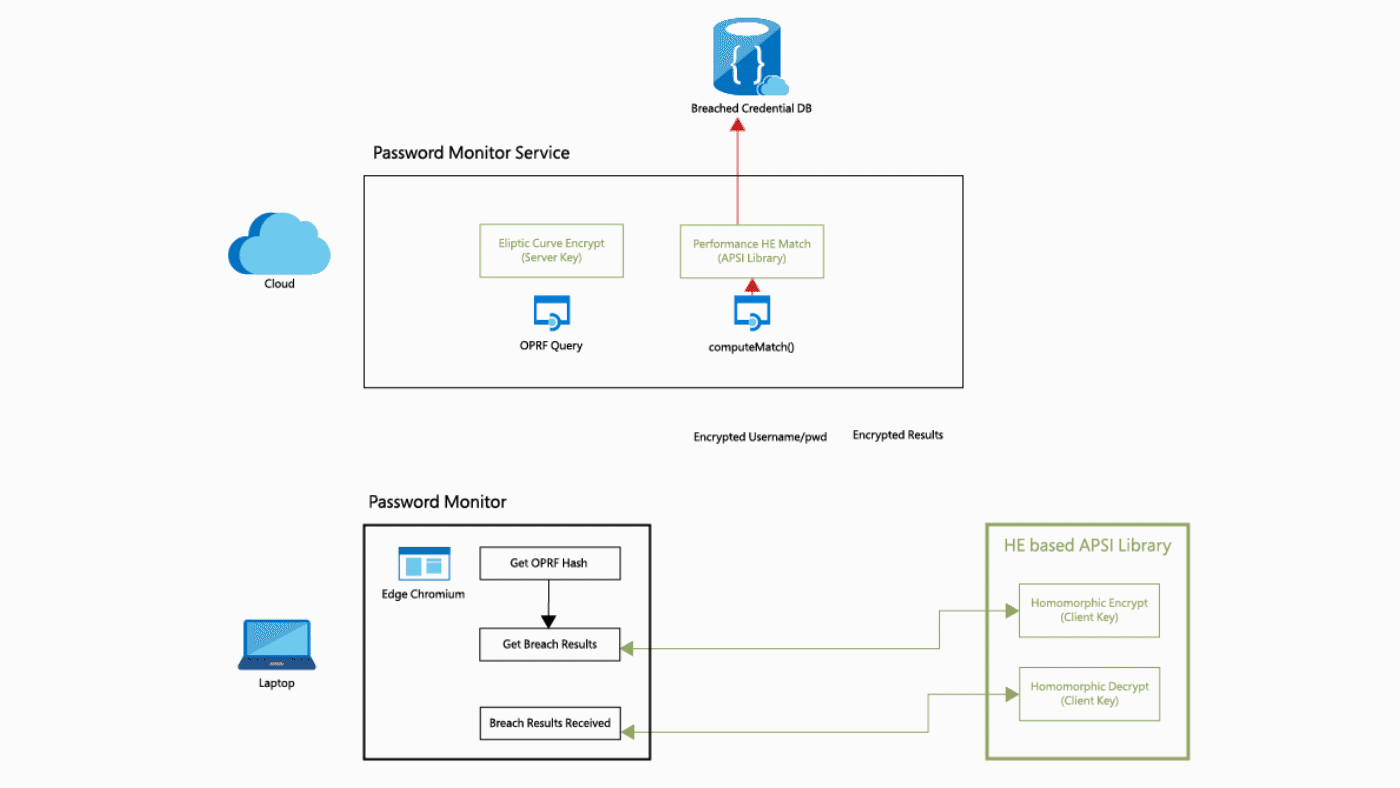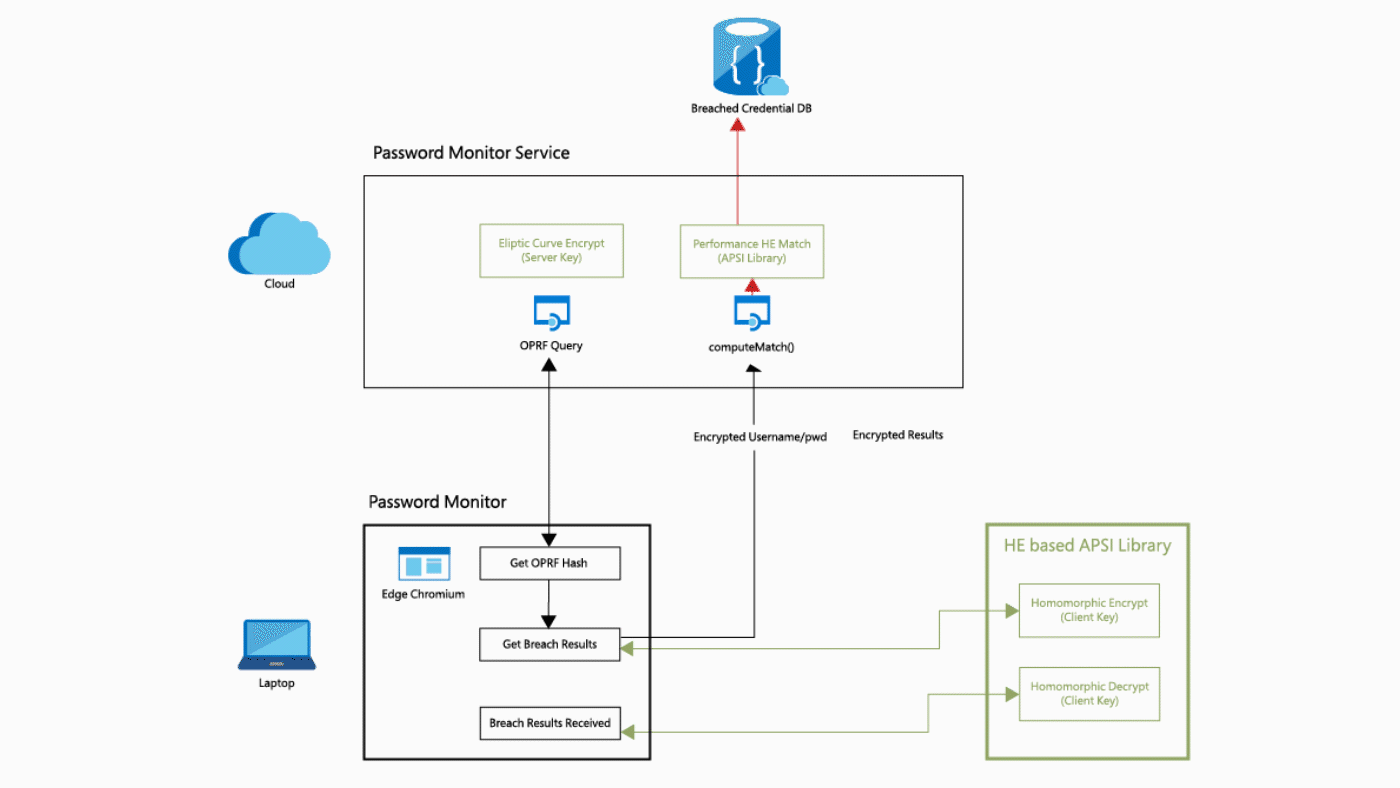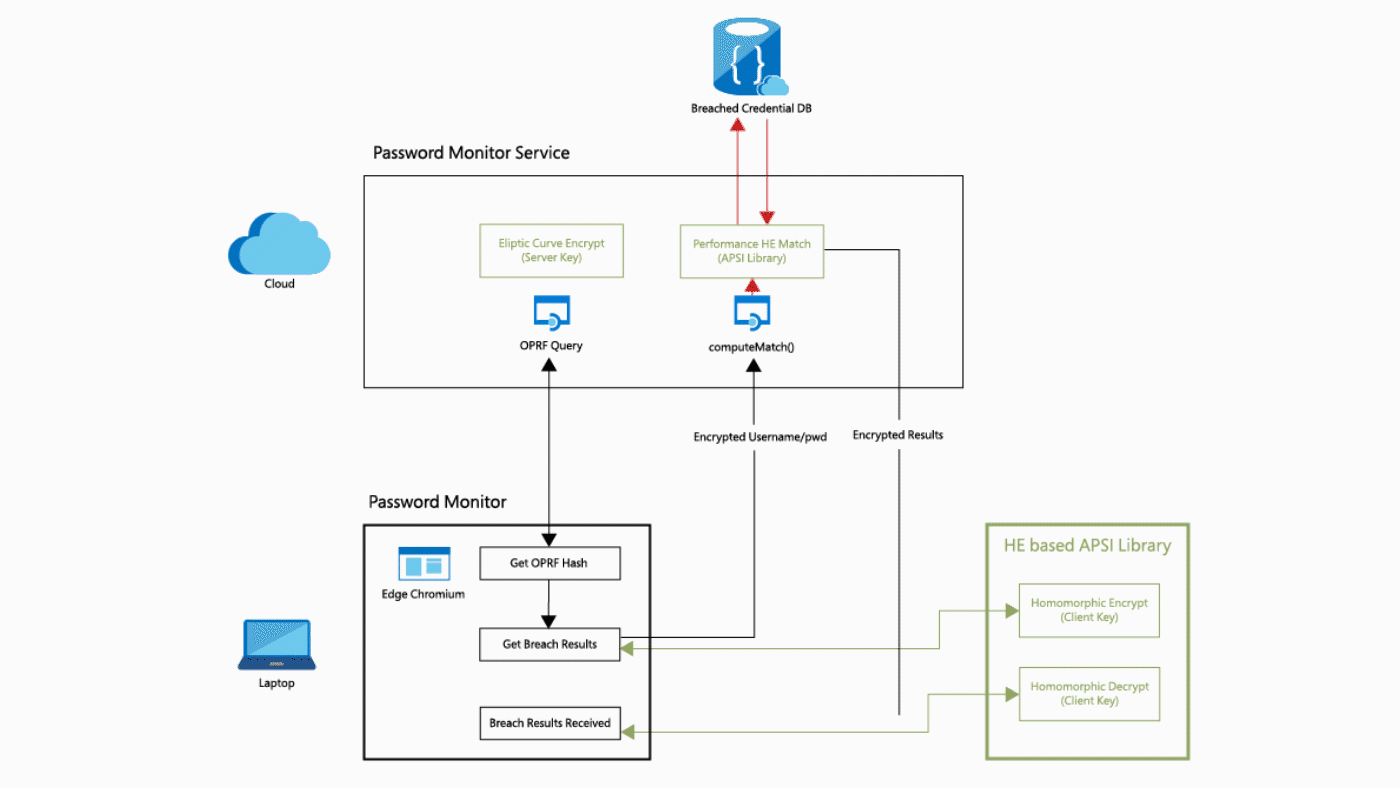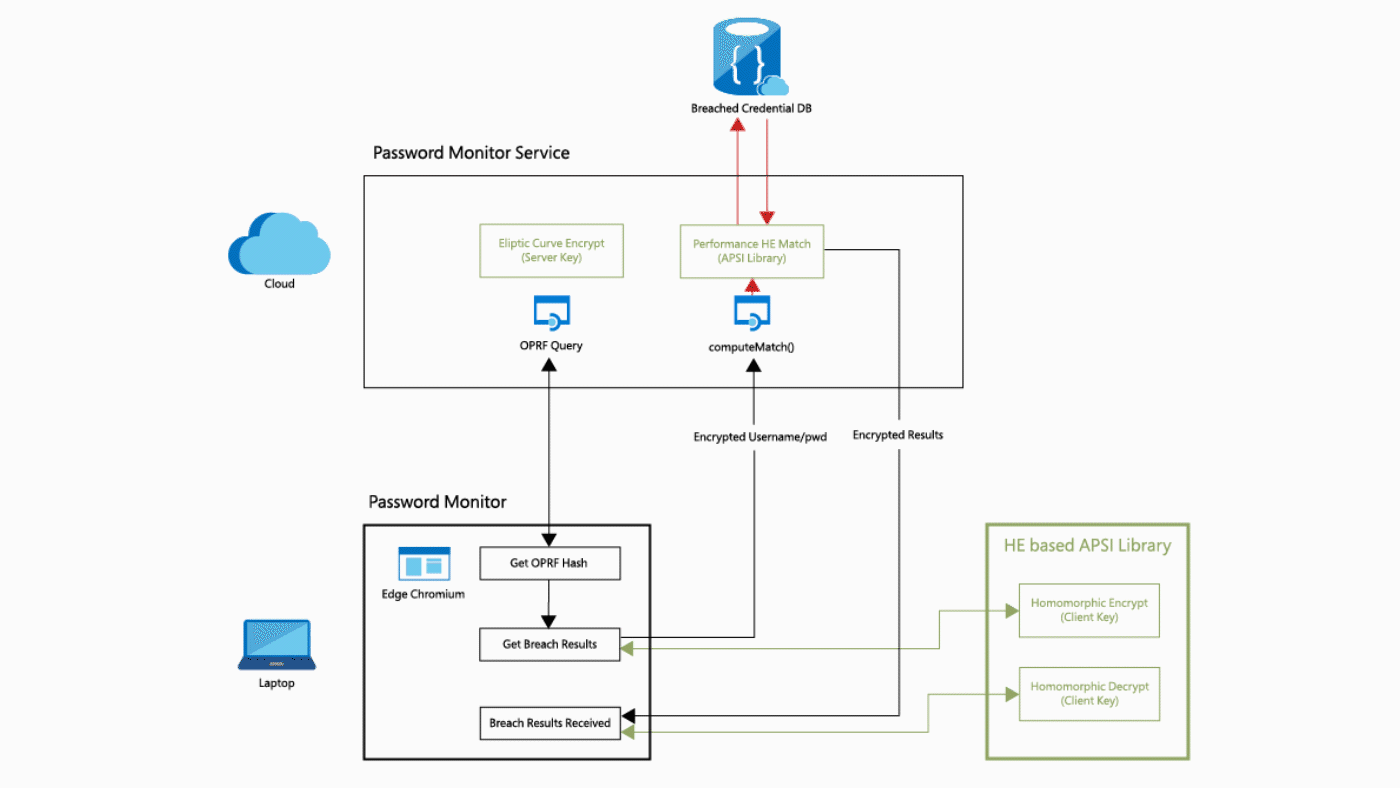
Today: Data is Encrypted Only During Communication

Privacy of user data is not guaranteed.
Privacy and Security Requirements in AI

...consent should be given for all purposes...
What are we trying to secure?



- Secure Data
- Both, input $x$ and outcome $f(x)$
- All intermediate computations are encrypted.
- Preserves user privacy.
- Secure Function
- $f$: parameters and architecture.
- All intermediate computations are encrypted.
- Preserves intellectual property and user privacy.
Example: Healthcare AI-based SaaS


However, both the data $x$ and the circuit $f$ are sensitive.
Securing User Data

Privacy of Alice's data is cryptographically guaranteed, but Bob has to give away his circuit to CCS.
Consequences of circuit cleartext FHE evaluation

-
Circuits are usually
- Proprietary functions (e.g., ML trained models)
- Directly derived from personal data (e.g., health data)
-
Circuits can be leaked from
- Noise term analysis
- Timing attacks
Circuit protection is also as crucial as data protection.
Privacy protection of both data and circuit

Today's Agenda
Is there an encryption scheme that satisfies our security requirements?
Fully Homomorphic Encryption
What is Fully Homomorphic Encryption?
Run programs on encrypted data without ever decrypting it.FHE can—in theory—handle universal computation.


Private Information Retreival
- Computational complexity $\mathcal{O}\left( K \cdot \left( \#\mathrm{M}_{\mathrm{HE}} + \#\mathrm{R}_{\mathrm{HE}} + \#\mathrm{A}_{\mathrm{HE}} \right) \right)$

Homomorphic Evaluation of Encrypted Data

- Packing
- Encoding
- Encryption
- Processing
Primitive Operations Supported by Arithmetic FHE Schemes




Main Idea: Noisy Inner Products

$\mathbf{s} = \begin{bmatrix}10 \\ 82 \\ 50 \\ 51\end{bmatrix}$
\[ \begin{align} 77w + 7x + 28y + 23z &= 2859 \text{ } \nonumber \\ 21w
+ 19x + 30y + 48z &= 3508 \text{ } \nonumber \\ 4w + 24x + 33y + 38z &=
3848 \text{ } \nonumber \\ 8w + 20x + 84y + 61z &= 6225 \text{ }
\nonumber \\ \end{align} \]
\[ \begin{align} 77w + 7x + 28y + 23z &= 2859 \text{ } \nonumber \\ 21w
+ 19x + 30y + 48z &= 3508 \text{ } \nonumber \\ 4w + 24x + 33y + 38z &=
3848 \text{ } \nonumber \\ 8w + 20x + 84y + 61z &= 6225 \text{ }
\nonumber \\ \end{align} \]
\[ \begin{align} 77w + 7x + 28y + 23z &= 2859 \text{ } \nonumber \\ 21w
+ 19x + 30y + 48z &= 3508 \text{ } \nonumber \\ 4w + 24x + 33y + 38z &=
3848 \text{ } \nonumber \\ 8w + 20x + 84y + 61z &= 6225 \text{ }
\nonumber \\ \end{align} \]
\[ \begin{align} 77w + 7x + 28y + 23z &= 2859 \text{ } \color{#ff8080}{
+ \text{ } (-3)} \nonumber \\ 21w + 19x + 30y + 48z &= 3508 \text{ }
\color{#ff8080}{ + \text{ } (+2)} \nonumber \\ 4w + 24x + 33y + 38z &=
3848 \text{ } \color{#ff8080}{ + \text{ } (-1)} \nonumber \\ 8w + 20x +
84y + 61z &= 6225 \text{ } \color{#ff8080}{ \underbrace{+ \text{ }
(+0)}_{noise}}\nonumber \\ \end{align} \]
\[ \begin{align} 77w + 7x + 28y + 23z &= 2859 \text{ } \color{#ff8080}{
+ \text{ } (-3)} \nonumber \\ 21w + 19x + 30y + 48z &= 3508 \text{ }
\color{#ff8080}{ + \text{ } (+2)} \nonumber \\ 4w + 24x + 33y + 38z &=
3848 \text{ } \color{#ff8080}{ + \text{ } (-1)} \nonumber \\ 8w + 20x +
84y + 61z &= 6225 \text{ } \color{#ff8080}{ \underbrace{+ \text{ }
(+0)}_{noise}}\nonumber \\ \end{align} \]
\[ \begin{align} 77w + 7x + 28y + 23z &= 2859 \text{ } \color{#ff8080}{
+ \text{ } (-3)} \color{cyan}{\text{ (mod 89)}} \nonumber \\ 21w + 19x +
30y + 48z &= 3508 \text{ } \color{#ff8080}{ + \text{ } (+2)}
\color{cyan}{\text{ (mod 89)}} \nonumber \\ 4w + 24x + 33y + 38z &= 3848
\text{ } \color{#ff8080}{ + \text{ } (-1)} \color{cyan}{\text{ (mod
89)}} \nonumber \\ 8w + 20x + 84y + 61z &= 6225 \text{ }
\color{#ff8080}{ \underbrace{+ \text{ } (+0)}_{noise}}\text{
}\color{cyan}{\underbrace{\text{(mod 89)}}_{ring}} \nonumber \\
\end{align} \]
\[ \begin{align} 77w + 7x + 28y + 23z &= 2859 \text{ } \color{#ff8080}{
+ \text{ } (-3)} \color{cyan}{\text{ (mod 89)}} \nonumber \\ 21w + 19x +
30y + 48z &= 3508 \text{ } \color{#ff8080}{ + \text{ } (+2)}
\color{cyan}{\text{ (mod 89)}} \nonumber \\ 4w + 24x + 33y + 38z &= 3848
\text{ } \color{#ff8080}{ + \text{ } (-1)} \color{cyan}{\text{ (mod
89)}} \nonumber \\ 8w + 20x + 84y + 61z &= 6225 \text{ }
\color{#ff8080}{ \underbrace{+ \text{ } (+0)}_{noise}}\text{
}\color{cyan}{\underbrace{\text{(mod 89)}}_{ring}} \nonumber \\
\end{align} \]
| Domain | Noise | Problem | Solution |
| $\mathbb{R}$ | $\times$ | System of Linear Equations | Gaussian Elimination |
| $\mathbb{R}$ | $\checkmark$ | Least Squares Problem | Least Squares Estimator |
| $\mathbb{Z}_q$ | $\checkmark$ | Learning with Errors Problem | Infeasible in Polynomial Time |
Encryption and Decryption


- a: fixed random vector
- e: noise from discrete Gaussian
- m: message
- s: private key
- $p=(a, b)$: public key with $b=\langle a,s \rangle + e$
- $\Delta$: scale factor
- Encryption: $c = (b + \Delta m) \text{ mod } q$
- Decryption: $\tilde{m} = round\left(\frac{c - \langle a,s \rangle}{\Delta}\right)$
Relies on hardness of the Learning with Errors problem.
Data Encoding

Operating with cyclotomic polynomials enables operations on vectors.\[ \begin{align} \text{Secret Key: } s &= s(x) \text{ sampled with coefficients from } \{-1, 0, 1\} \nonumber \\ \text{Public Key: } p &= (a(x), b(x)) \nonumber \\ \text{with } a(x) &= \text{ random polynomial sampled from } \mathbb{Z}_q[x]/(x^N+1) \nonumber \\ \text{with } b(x) &= (\langle a(x), s(x) \rangle + e) \text{ mod } \mathbb{Z}_q[x]/(x^N+1) \nonumber \end{align} \]
- message: $m(x)$ polynomial in $\mathbb{Z}_q[x]/(x^N+1)$
- Encryption: $c(x) = b(x) + \Delta m(x) \text{ mod } \mathbb{Z}_q[x]/(x^N+1)$
- Decryption: $\tilde{m}(x) = (c(x) - \langle a(x), s(x) \rangle)/\Delta$
Data Packing






- Packing affects computation cost significantly.
- Many advanced packing schemes exist.
Data Privacy
Data and Circuit Privacy
AutoFHE
Co-Designing AI and Homomorphic Architectures
- Security Requirement
Encryption Parameters
- Cyclotomic polynomial degree: $N$
- Level: $L$
- Modulus: $Q_l=\prod_{i=0}^{l} q_l, 0 \leq q_l \leq L$
- Bootstrapping Depth: $K$
- Hamming Weight: $h$
- Latency
- Prediction Accuracy
Polynomial CNNs
- Conv, BN, pooling, FC layers: packing
- Polynomials: degree -> depth
- Number of layers: ResNet20, ResNet32
- Input image resolution
- Channels/kernels
CNNs under Homomorphic Encryption









- Multiplication
- Addition
- Rotation
Deep CNNs under Homomorphic Encryption








- Level: number of allowed multiplications
Drawbacks of bootstrapping: high latency and high memory footprint
Polynomial Neural Architectures




How to effectively trade-off between accuracy and latency?
Our Key Insight
How to optimize end-to-end polynomial neural architecture?
Joint Search for Layerwise EvoReLU and Bootstrapping Operations



- Flexible Architecture
- On demand Bootstrapping
Bi-Level Multi-Objective Framework

Experimental Setup
Dataset: CIFAR10
- 50,000 training images
- 10,000 test images
- 32x32 resolution, 10 classes
Hardware & Software
- Amazon AWS, r5.24xlarge
- 96 CPUs, 768 GB RAM
- Microsoft SEAL, 3.6
Latency and Accuracy Trade-offs under FHE




| Approach | MPCNN | AESPA | REDsec | AutoFHE |
|---|---|---|---|---|
| Venue | ICML22 | arXiv22 | NDSS23 | USENIX24 |
| Scheme | CKKS | CKKS | TFHE | CKKS |
| Polynomial | high | low | n/a | mixed |
| Layerwise | No | No | n/a | Yes |
| Strategy | approx | train | train | adapt |
| Architecture | manual | manual | manual | search |
- MPCNN: Low-Complexity Convolutional Neural Networks on Fully Homomorphic Encryption Using Multiplexed Parallel Convolutions, ICML 2022
- AESPA: Accuracy Preserving Low-degree Polynomial Activation for Fast Private Inference, arXiv 2022
- REDsec: Running Encrypted Discretized Neural Networks in Seconds, NDSS 2023
- AutoFHE: Automated Adaption of CNNs for Efficient Evaluation over FHE, USENIX Security 2024
Data Privacy
Data and Circuit Privacy
CryptoFace
What are the privacy and security risks in Face Recognition?












Prior Work: Template Protection
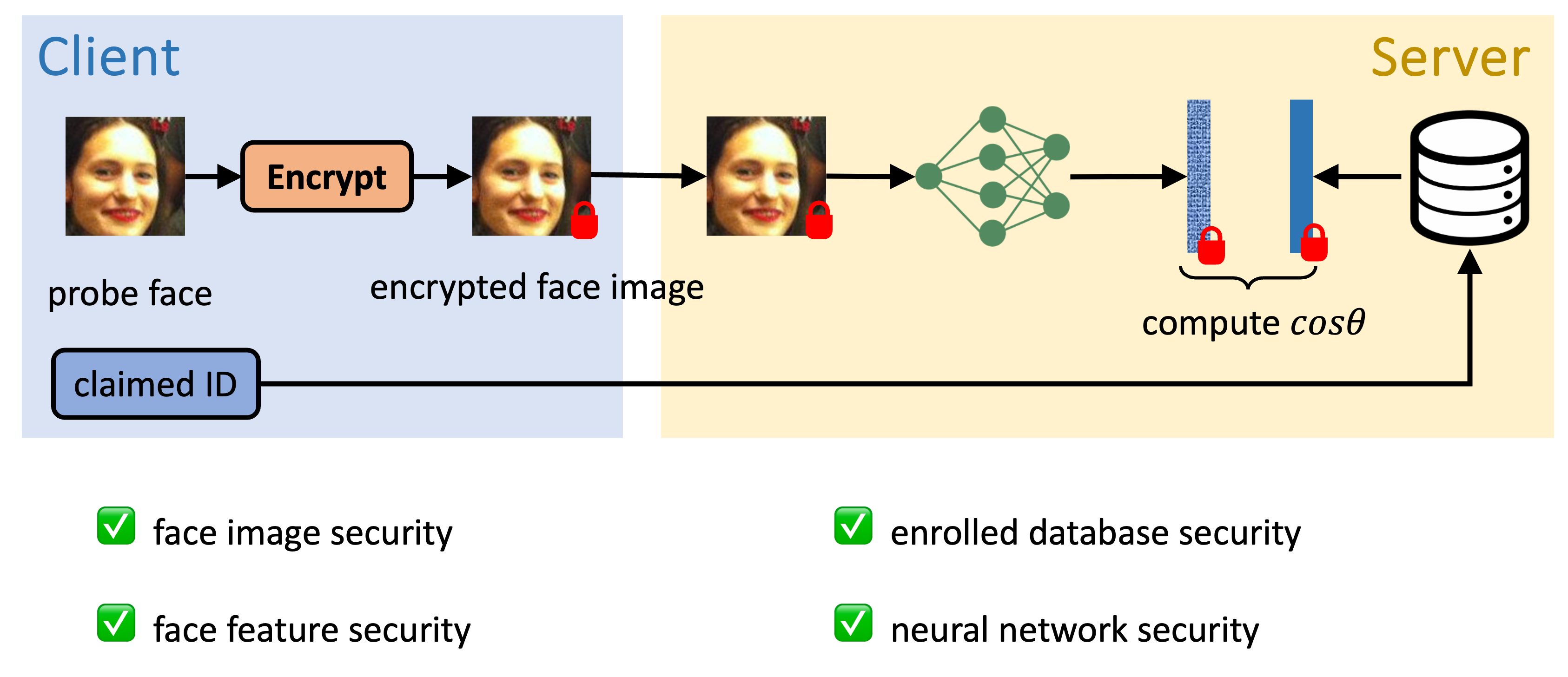
End-to-End Encrypted Face Recognition
Offline Enrollment
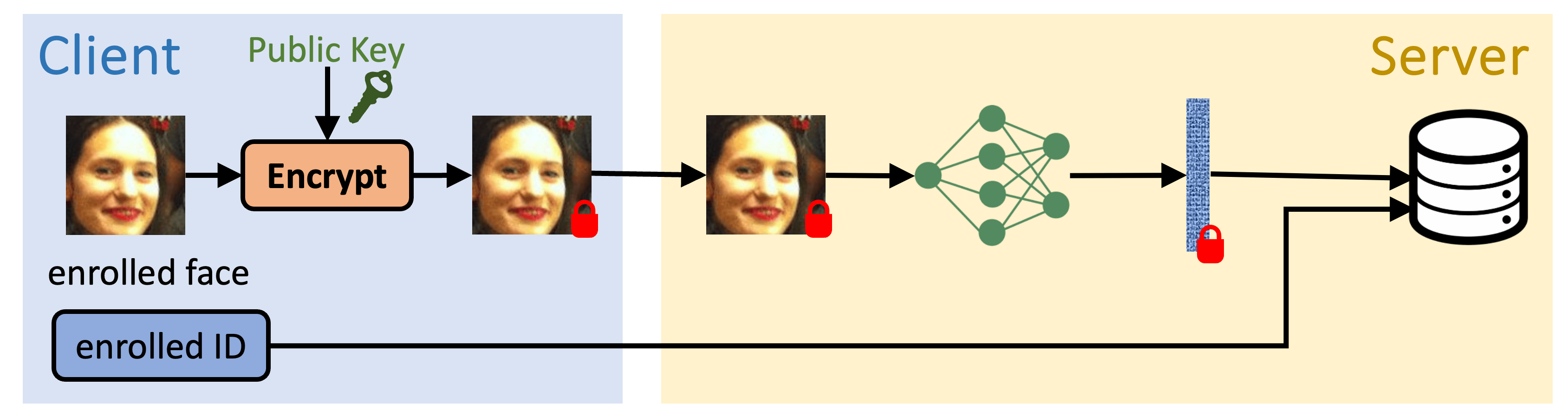
Online Verification
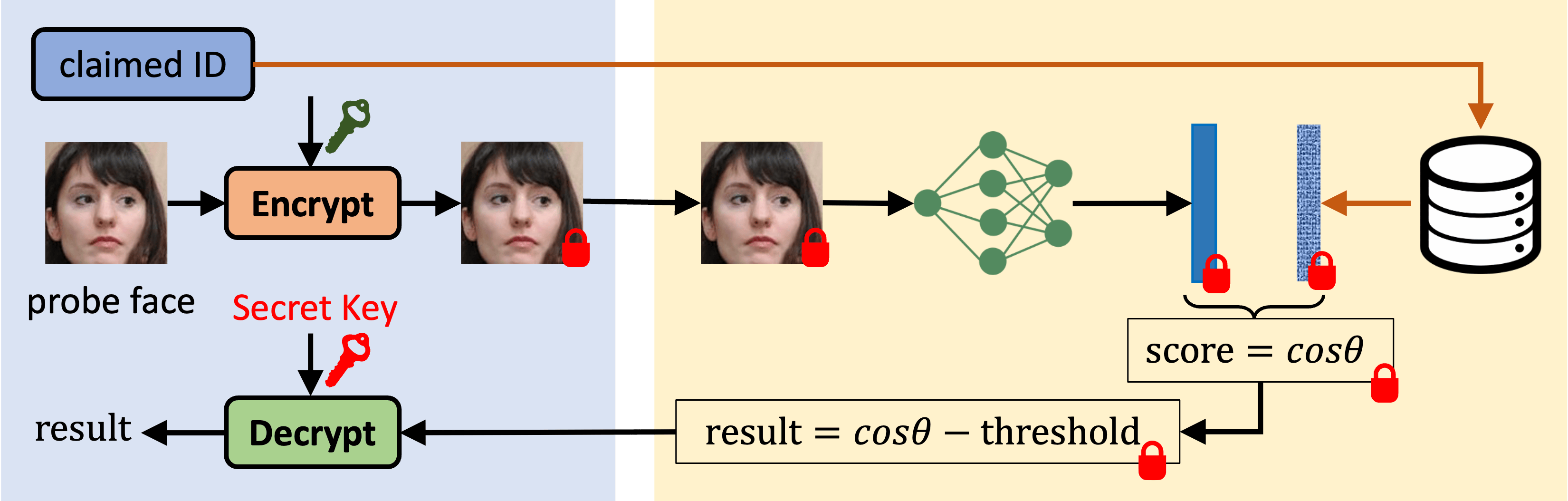
Challenges of End-to-End Encrypted Face Recognition
- Face recognition typically uses 112x112 images.
-
Encryption slot size is typically $16,384$.
- Prior work processes 32x32 images.
- Cannot encode and process high-resolution images.
- Increases computational costs.
Rethink neural and homomorphic architecture designs.
Key Idea: Mixture of Shallow Patch CNNs
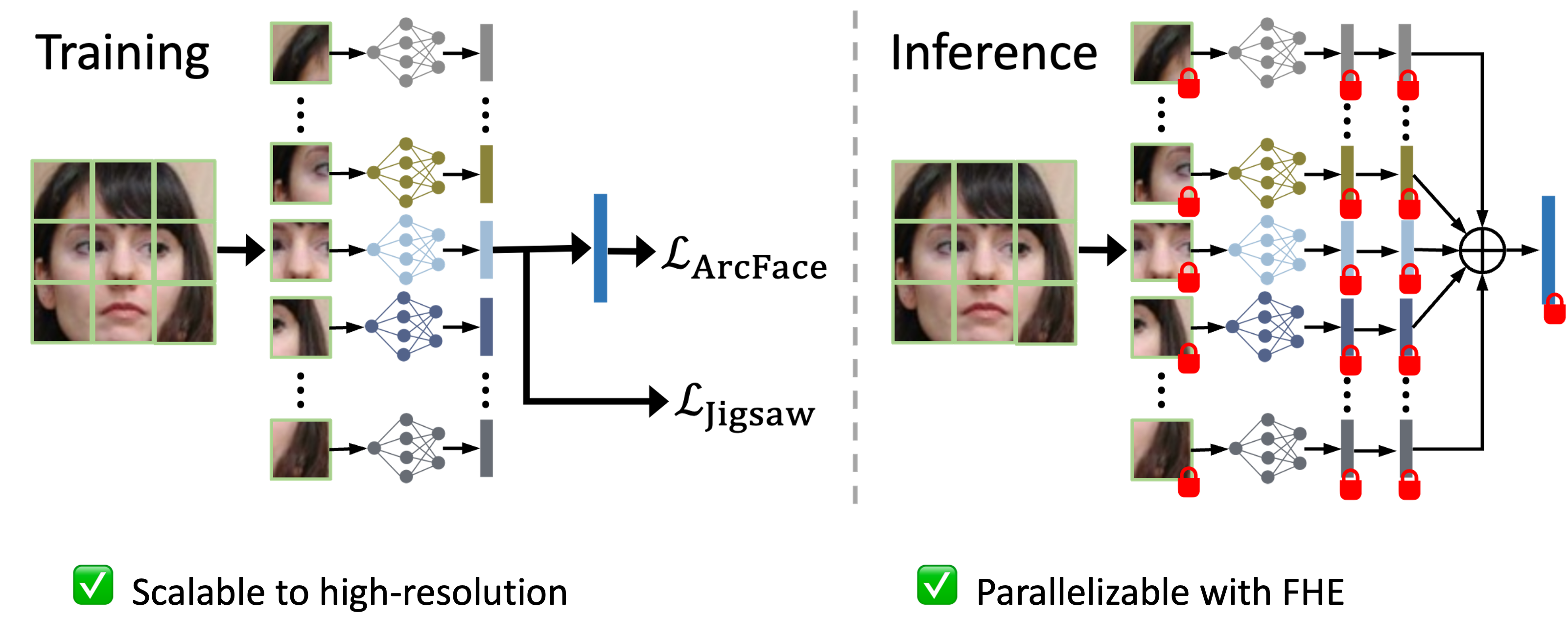
Homomorphic Level Optimal Block

CryptoFace Architecture
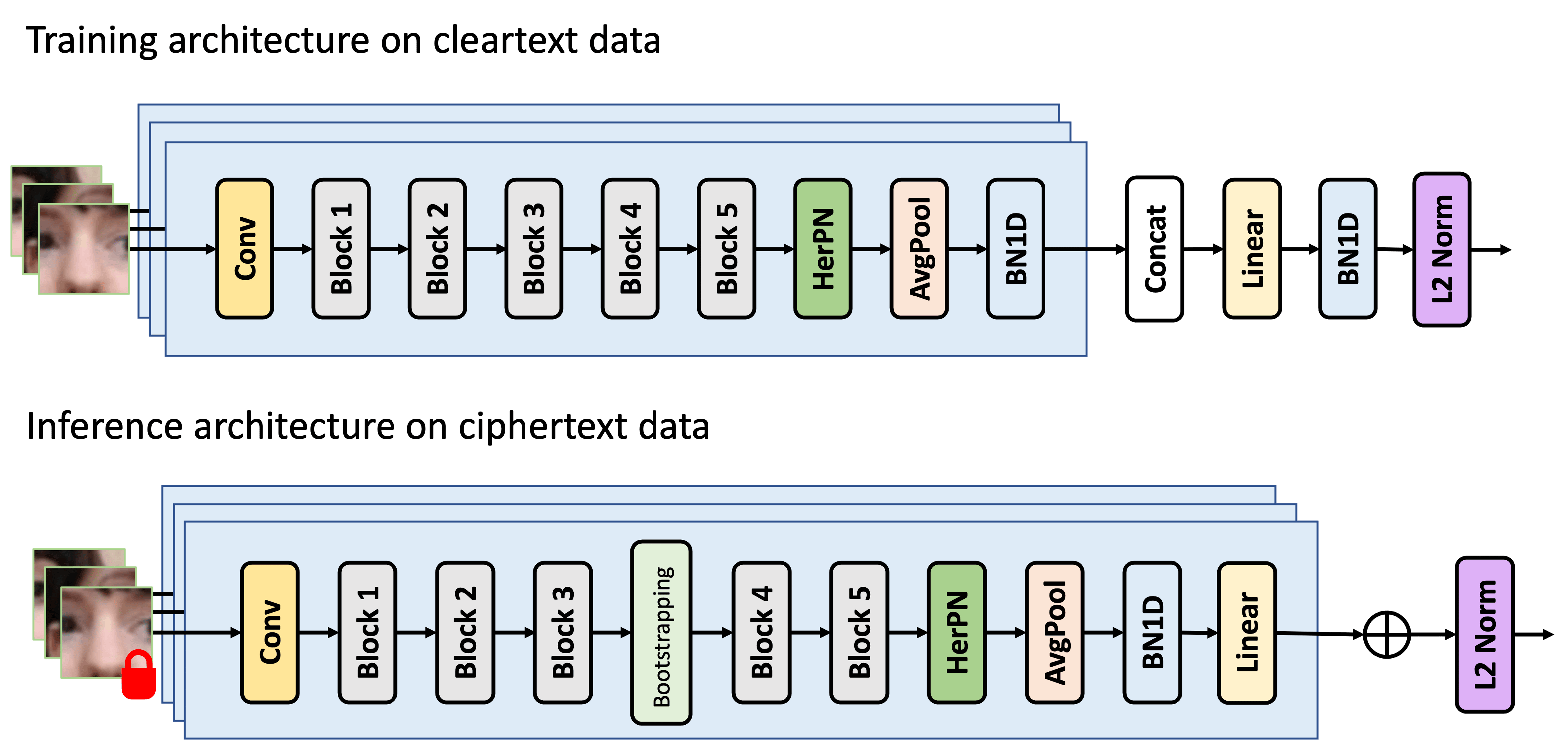
Polynomial Feature Normalization
- L2 Normalization: $\tilde{\mathbf{y}} = \frac{\mathbf{y}}{\|\mathbf{y}\|_2} = \mathbf{y}\cdot \frac{1}{\sqrt{\sum_{i=1}^d}y_i^2}=\mathbf{y}\cdot q\left(\sqrt{\sum_{i=1}^d}y_i^2\right)$ (cannot be computed in CKKS)
- Our Solution: Approximate $q(t)=\frac{1}{\sqrt{t}}$ using a polynomial $p(t)=\beta_2t^2 + \beta_1t + \beta_0$

Cosine Similarity Under Encryption

- Cosine similarity: $$s(\mathbf{x},\mathbf{y}) = \frac{\mathbf{x}^T\mathbf{y}}{\|\mathbf{x}\|\|\mathbf{y}\|}$$
- For normalized $\mathbf{\tilde{x}}$ and $\mathbf{\tilde{y}}$, cosine becomes inner product (IP): $$< \mathbf{\tilde{x}},\mathbf{\tilde{y}}> = \sum_{i=1}^{d} \tilde{x_i} \tilde{y_i}$$
Requires $1$ multiplication and $\log_2(d)$ rotations and additions.
Experiments on Encrypted Face Datasets
Hardware & Software
- Amazon AWS, r5.24xlarge
- 96 CPUs, 768 GB RAM
- Microsoft SEAL, 3.6

| Approach | Backbone | Dataset | Latency(s) | Memory(GB) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Network | Params | Boot | LFW | AgeDB | CALFW | CPLFW | CFP-FP | Avg | |||
| MPCNN | ResNet32 | 529K | 31 | 97.02 | 83.02 | 87.00 | 78.90 | 82.07 | 85.60 | 7,367 | 286 |
| ResNet44 | 724K | 43 | 98.27 | 87.45 | 90.85 | 83.72 | 87.90 | 89.64 | 9,845 | 286 | |
| AutoFHE1 | ResNet32 | 531K | 8 | 93.53 | 80.88 | 85.40 | 75.67 | 77.96 | 82.69 | 4,001 | 286 |
| CryptoFace | PCNNs | 3.78M | 1 | 98.78 | 92.90 | 93.73 | 83.95 | 87.94 | 91.46 | 1,446 | 277 |
- Architecture searched on CIFAR10.↩
8x speedup from custom neural network design
Computational Cost Per Operation
| Approach | Backbone | Conv | BN | Residual | AvgPool | Linear | Activation | Norm | Score | Boot | Other |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPCNN | ResNet32 | 896 (12.17%) | 28 (0.38%) | 0.5 (0.01%) | 46 (0.62%) | 807 (10.96%) | 583 (7.92%) | 5 (0.07%) | 2 (0.02%) | 4991 (67.76%) | 7 (0.09%) |
| ResNet44 | 1214 (12.33%) | 39 (0.39%) | 0.7 (0.01%) | 46 (0.46%) | 807 (8.19%) | 807 (8.20%) | 5 (0.05%) | 2 (0.02%) | 6917 (70.27%) | 7 (0.08%) | |
| AutoFHE$^\dagger$ | ResNet32 | 1966 (49.13%) | 28 (0.69%) | 1.7 (0.04%) | 38 (0.95%) | 658 (16.43%) | 17 (0.43%) | 4 (0.10%) | 1 (0.03%) | 1274 (31.84%) | 14 (0.34%) |
| CryptoFace | PCNNs | 858 (62.93%) | 2 (0.16%) | 0.1 (0.01%) | 26 (1.94%) | 277 (20.30%) | 13 (0.94%) | 2 (0.11%) | 0.3 (0.02%) | 141 (10.34%) | 44 (3.26%) |
Resolution Scalability

Data Privacy
Data and Circuit Privacy
PrivaCT
Circuit Protection: Prior Solutions
- Inference under encryption to not share the circuit
- Restricted two-party scenario
- Cleartext evaluation of the circuit

Is the circuit protected?
-
No, noise term can leak it!
-
Circuit leakage prevention
- Elimination of the noise term (e.g., noise flooding, bootstrapping, etc.)
- Randomization of the evaluated ciphertext
PrivaCT:Data and Circuit Privacy
Goal: Reduce all functions to a uniform external circuit (inner products).

Key Idea of PrivaCT: Two-Stage Function Approximation

PrivaCT improves accuracy for a fixed computational complexity
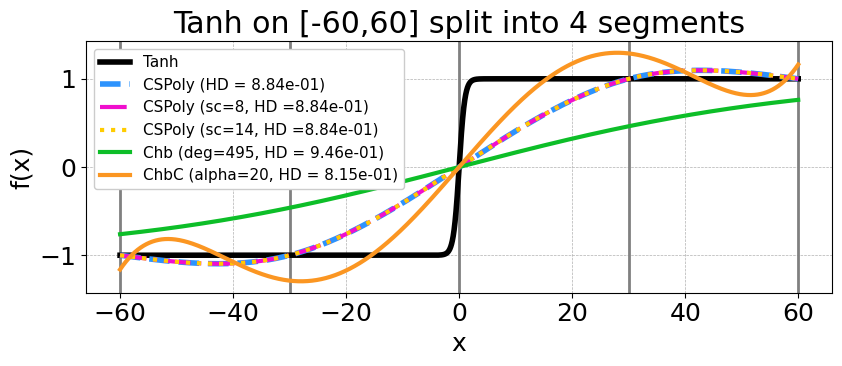
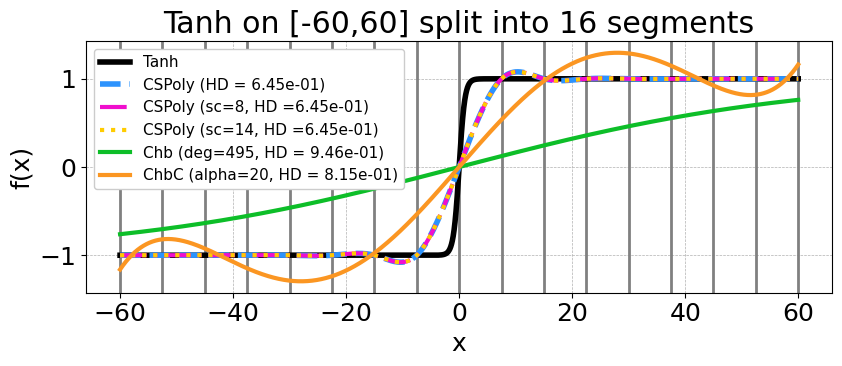
- Existing approaches require increasing their polynomial degree to improve the approximation performance
- Chebyshev approximation (green curves) $(deg=495)$ [BF24]
- Minmax composite Chebyshev approximation (orange curves) $(degrees = [5,5,5,7,7,7,7,7,27])$ [LL+21]
-
PrivaCT's approximation improves as the number of segments $(n_{seg})$
increases for a fixed degree $deg=3$
- It reaches the lowest Hausdorff distance $(HD = 0.645)$ at $n_{seg}=16$.
PrivaCT adapts with the function's subtle curvatures.
Runtime comparison between PrivaCT and state-of-the-art solutions
No loss in accuracy while achieving data and circuit privacy while significantly reducing runtime.
Story So Far...
Co-designing AI and FHE architectures is critical for efficiency.
Missing Piece in the Puzzle
Hardware Accelerators for FHE
Concluding Remarks
- Homomorphic encryption is the key to realizing end-to-end encrypted AI systems.
- Can realize both data and function privacy.
- Offers post-quantum security.
- Naive application of HE for AI suffers from prohibitive computational costs.
- Co-designing AI and Homomorphic architectures is critical for efficiency.
- Can get at least 10x speed up.
Exciting research at the intersection of AI, Cryptography, and ASIC Design.