Rethinking AI Architectures for Data and Circuit Privacy
AMS Special Session on AI meets Cryptography
Michigan State University
Progress In Artificial Intelligence
Speech Processing
Image Analysis
Natural Language Processing
Physical Sciences
State-of-Affairs
(report from the real-world)
Sep 19, 2024
Healthcare Data Breaches of 500+ Records (2009-2024)
Goal
Protect AI systems using FHE
What are we trying to protect in AI?

- $x$: images, audio, video, text
- $f$: parameters, functional form
Data Privacy

- Protect user privacy.
- Prevent unauthorized access.
- Gain user's trust.
- Comply with regulations like GDPR.
Function Privacy

- Protect intellectual property.
- Prevent attacks against model.
- Prevent leakage of training data.
- Comply with industry security standards.
Data Privacy vs Function Privacy


Neural Network Architectures for Data Privacy
Existing Solutions: Adapt CNNs for FHE









- Multiplication
- Addition
- Rotation
Only replace non-linear activations with polynomials.
Existing Solutions: Polynomial Neural Architectures




| Approach | MPCNN | AESPA | REDsec | AutoFHE |
|---|---|---|---|---|
| Venue | ICML22 | arXiv22 | NDSS23 | USENIX24 |
| Scheme | CKKS | CKKS | TFHE | CKKS |
| Polynomial | high | low | n/a | mixed |
| Layerwise | No | No | n/a | Yes |
| Strategy | approx | train | train | adapt |
| Architecture | manual | manual | manual | search |
Limited scope for large computational efficiencies from minor modifications of existing architectures (about 2x-3x).
- MPCNN: Low-Complexity Convolutional Neural Networks on Fully Homomorphic Encryption Using Multiplexed Parallel Convolutions, ICML 2022
- AESPA: Accuracy Preserving Low-degree Polynomial Activation for Fast Private Inference, arXiv 2022
- REDsec: Running Encrypted Discretized Neural Networks in Seconds, NDSS 2023
- Wei Ao and Vishnu Boddeti, AutoFHE: Automated Adaption of CNNs for Efficient Evaluation over FHE, USENIX Security 2024
Outstanding Challenges for Image Recognition Tasks
- Want to process larger images.
- 112x112 for face recognition
- 256x256 for image classification
-
Encryption slot size is typically $16,384$.
- Prior work processes 32x32 images.
- Cannot encode and process high-resolution images.
- Increases computational costs.
Rethink neural and homomorphic architecture designs.
Architecture Design Preferences
| Concept | Conventional | FHE Compatible | Benefits |
|---|---|---|---|
| model depth | deep | shallow | reduce multiplicative depth |
| resolution scalability | single big network | multiple small networks | exploit parallelism |
| layer sequence | performance driven | efficiency driven | level optimality |
Case Study: CryptoFace
What are the privacy and security risks in Face Recognition?


Prior Work: Template Protection
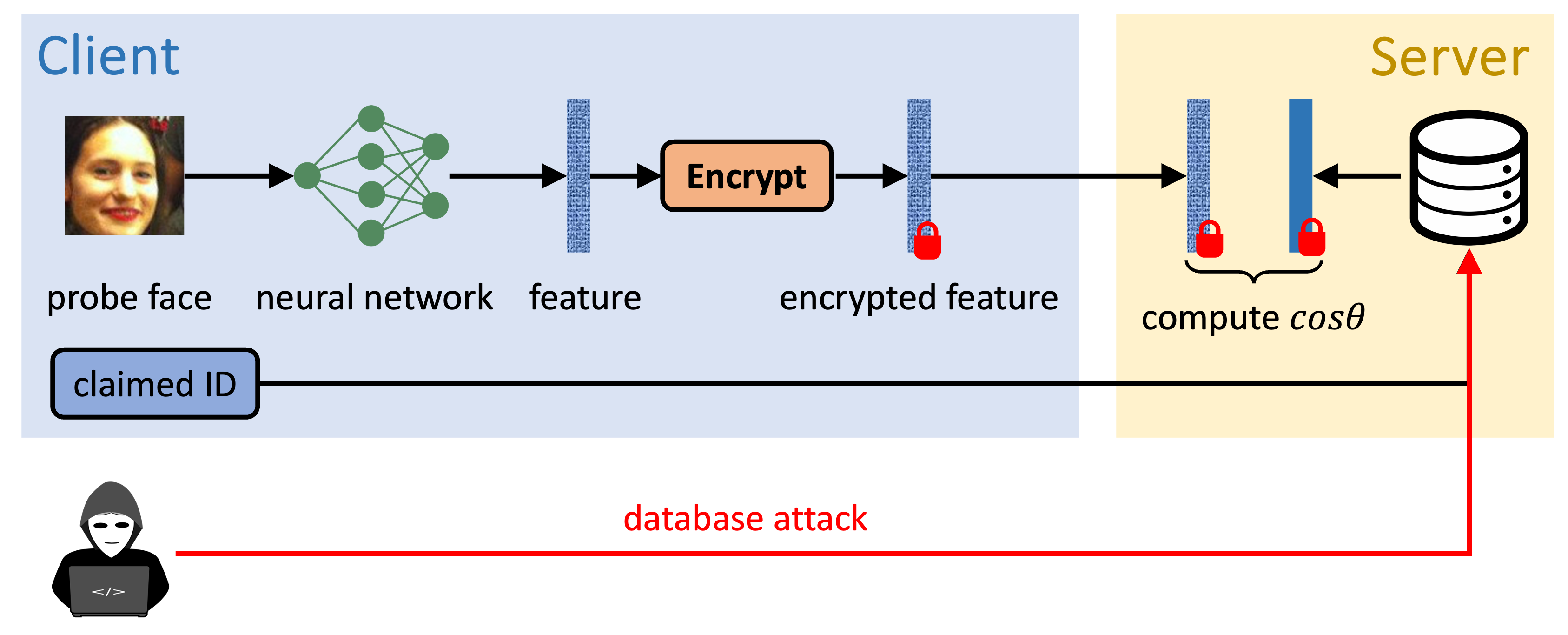
End-to-End Encrypted Face Recognition

Mixture of Shallow Patch CNNs
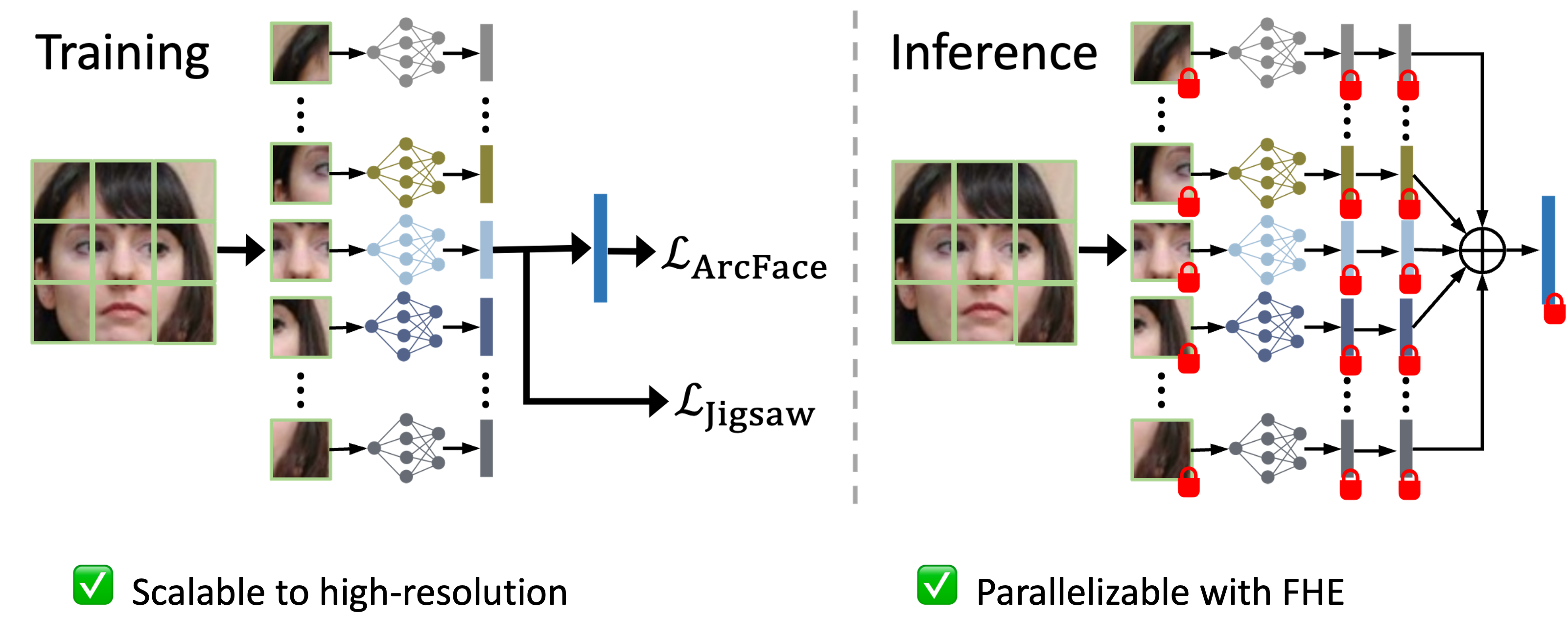
Homomorphic Level Optimal Block

Encrypted Face Recognition Evaluation
Hardware & Software
- Amazon AWS, r5.24xlarge
- 96 CPUs, 768 GB RAM
- Microsoft SEAL, 3.6

| Approach | Resolution | Backbone | Six Datasets | Latency(s) | Memory(GB) | ||
|---|---|---|---|---|---|---|---|
| Network | Params | Boot | Avg Accuracy | ||||
| AdaFace (non-FHE SOTA) | 112x112 | ResNet100 | 529K | NA | 97.51 | NA | NA |
| MPCNN | 64x64 | ResNet32 | 529K | 31 | 85.60 | 7,367 | 286 |
| 64x64 | ResNet44 | 724K | 43 | 89.64 | 9,845 | 286 | |
| AutoFHE1 | 64x64 | ResNet32 | 531K | 8 | 82.69 | 4,001 | 286 |
| CryptoFace | 64x64 | PCNNs | 944K | 1 | 89.42 | 1,364 | 269 |
| CryptoFace | 96x96 | PCNNs | 2,124K | 1 | 90.99 | 1,395 | 276 |
- Architecture searched on CIFAR10.↩
8x speedup from custom neural network design
Computational Cost Per Operation
| Approach | Backbone | Conv | BN | Residual | AvgPool | Linear | Activation | Norm | Score | Boot | Other |
|---|---|---|---|---|---|---|---|---|---|---|---|
| MPCNN | ResNet32 | 896 (12.17%) | 28 (0.38%) | 0.5 (0.01%) | 46 (0.62%) | 807 (10.96%) | 583 (7.92%) | 5 (0.07%) | 2 (0.02%) | 4991 (67.76%) | 7 (0.09%) |
| ResNet44 | 1214 (12.33%) | 39 (0.39%) | 0.7 (0.01%) | 46 (0.46%) | 807 (8.19%) | 807 (8.20%) | 5 (0.05%) | 2 (0.02%) | 6917 (70.27%) | 7 (0.08%) | |
| AutoFHE$^\dagger$ | ResNet32 | 1966 (49.13%) | 28 (0.69%) | 1.7 (0.04%) | 38 (0.95%) | 658 (16.43%) | 17 (0.43%) | 4 (0.10%) | 1 (0.03%) | 1274 (31.84%) | 14 (0.34%) |
| CryptoFace | PCNNs | 858 (62.93%) | 2 (0.16%) | 0.1 (0.01%) | 26 (1.94%) | 277 (20.30%) | 13 (0.94%) | 2 (0.11%) | 0.3 (0.02%) | 141 (10.34%) | 44 (3.26%) |
Architectures for Data and Function Privacy
Example: Healthcare AI-based SaaS


Both the data $x$ and the function $f$ are sensitive.
Function Privacy: Existing Approach

Is the function protected? No, noise term can leak it!
Function Privacy: Existing Approach

- Preventing function leakage
- Obfuscate the noise term.
- noise flooding
- bootstrapping
- Randomize the input.
- add noise
Securing User Data

Privacy of Alice's data is cryptographically guaranteed, but Bob has to give away his function to CCS.
Privacy protection of both data and function

Case Study: PrivaCT
PrivaCT
Transform internal circuit to a uniform, but, equivalent external circuit.

Preliminary Solution: Two-Stage Approximation







| Property | Value |
|---|---|
| Data | encrypted |
| Function | encrypted |
| External Circuit | inner product |
| Evaluation | constant w.r.t in/out dim |
Step 1: Use RBF kernel as a universal function approximator
- Kernel-based function approximation: $$\hat{f}(x) = \sum_{i=1}^{n} \alpha_{i} K(x,
x_i)
+ \bar{b}$$
- We adopt RBF kernels $K(x,x_i) = \exp(-\gamma \|x-x_i\|^2)$
- Decompose RBF kernel into scalar functions:
- $K(x,x_i) = \underbrace{\exp\big(-\gamma \|x\|^2\big)}_{\text{scalar function}} \times \underbrace{\exp\big(-\gamma \|x_i\|^2\big)}_{\text{constant}} \times \underbrace{\prod_{j=1}^{d} \exp(2\gamma x_{i,j} \cdot x_j)}_{\text{product of scalar functions}}$
$$ K(x,x_i) = \tilde{g_i}(\|x\|^2) \times \prod_{j=1}^{d} g_{i,j}(x_j) $$
Step 2: Function Evaluation through Inner Products
- Key Ideas:
- segment the domain
- piecewise low-degree polynomial approximation $$P(X) = \nu_0 + \nu_1 X + \cdots + \nu_n X^n$$
- polynomial evaluation using inner product $$P(X) = \langle \vec{\nu}, \vec{X} \rangle \text{ where } \vec{\nu} = (\nu_0,\nu_1, \cdots,\nu_n) \text{ and } \vec{X} = (1, X, \cdots,X^n)$$



- Benefits:
- Low-complexity function supporting FHE evaluation using SIMD property.
- Operands can be independently encrypted.
- Constant-time function evaluation in FHE.
- prevents timing attacks
PrivaCT: Scalar function evaluation

PrivaCT: Vector functions evaluation
Custom data packing for vector functions.

PrivaCT improves accuracy for a fixed computational complexity


- Existing approaches: high-degree/composite polynomials
- Chebyshev approximation (green curves) $(deg=495)$ [BF24]
- Minmax composite Chebyshev approximation (orange curves) $(degrees = [5,5,5,7,7,7,7,7,27])$ [LL+21]
- PrivaCT's approximation improves with number of segments
$(n_{seg})$ for a fixed
degree $deg=3$.
- Achieves lowest Hausdorff distance $(HD = 0.645)$ at $n_{seg}=16$.
PrivaCT adapts with the function's subtle curvatures.
PrivaCT preserves accuracy
Runtime comparison between PrivaCT and state-of-the-art solutions
Affords data and function privacy while also significantly reducing runtime.
Story So Far...
Co-designing AI and FHE architectures is critical for efficiency.
Missing Piece in the Puzzle
Hardware Accelerators for FHE
Concluding Remarks
- Data and function privacy are critical for real-world AI systems.
- End-to-end encrypted AI systems with FHE are feasible.
- Both data and function privacy can be realized.
- Offers strong guarantees.
- Naive application of HE for AI suffers from prohibitive computational costs.
- Rethinking AI architecture designs is critical for efficiency.
- Can get at least 10x speed up.
Exciting research at the intersection of AI, Cryptography, and ASIC Design.