Towards Semantically Controllable and Secure Representations

Purdue University

Vishnu Boddeti

September 14, 2020

VishnuBoddeti

Progress In Biometrics

State-of-Affairs

Today's Agenda

100 Years of Data Representations

Bias in Learning

• Training:
• Inference: Microsoft Gender classification



lighter faces: 0.7% error


darker faces: 12.9% error

Privacy Leakage

• Training:
• Inference: Microsoft Smile classification



• Target Task
• Smile: 93.1%


• Privacy Leakage
• Gender: 82.9%

Information Leakage from Representations

• Learned Embeddings:
• Attacks on Embeddings:
Face reconstruction from template



Privacy leakage through attribute prediction from template

Recklessly absorb all statistical correlations in data

Next Era of Biometric Representations

Controlling Semantic Information

• Target Concept: Smile & Private Concept: Gender

• Problem Definition:
• Learn a representation $\mathbf{z} \in \mathbb{R}^d$ from data $\mathbf{x}$
• Retain information necessary to predict target attribute $\mathbf{t}\in\mathcal{T}$
• Remove information related to a desired sensitive attribute $\mathbf{s}\in\mathcal{S}$

Technical Challenge

• How to explicitly control semantic information in learned representations?



• Can we explicitly control semantic information in learned representations?

A Subspace Geometry Perspective

• Case 1: when $\mathcal{S} \perp \!\!\! \perp \mathcal{T}$ (Gender, Age)

• Case 3: when $\mathcal{S} \sim \mathcal{T}$ ($\mathcal{T}\subseteq\mathcal{S}$)

A Fork in the Road

• Design metric to measure semantic attribute information
• not obvious how



• Learn metric to measure semantic attribute information
• probably feasible

Game Theoretic Formulation

• Three player game between:
• Encoder extracts features $\mathbf{z}$
• Target Predictor for desired task from features $\mathbf{z}$
• Adversary extracts sensitive information from features $\mathbf{z}$
\begin{equation} \begin{aligned} \min_{\mathbf{\Theta}_E,\mathbf{\Theta}_T} & \underbrace{\color{cyan}{J_t(\mathbf{\Theta}_E,\mathbf{\Theta}_T)}}_{\color{cyan}{\mbox{error of target}}} \quad s.t. \mbox{ } \min_{\mathbf{\Theta}_A} \underbrace{\color{orange}{J_s(\mathbf{\Theta}_E,\mathbf{\Theta}_A)}}_{\color{orange}{\mbox{error of adversary}}} \geq \alpha \nonumber \end{aligned} \end{equation}
• Adversary: learned measure of semantic attribute information

How do we learn model parameters?

• Simultaneous/Alternating Stochastic Gradient Descent
• Update target while keeping encoder and adversary frozen.
• Update adversary while keeping encoder and target frozen.
• Update encoder while keeping target and adversary frozen.

Three Player Game: Linear Case

• Global solution is $(w_1, w_2, w_3)=(0, 0, 0)$

Our Contributions

• Non-Zero Sum Formulation for Iterative Methods (CVPR'19)
• Standard setting, each player is a deep neural network.
• Local optima


• Global Optima for Kernel Methods (ICCV'19)
• Simplified setting, each player is linear.
• closed form solution + stable + performance bounds


• Hybrid Model with CNNs and Closed-Form Solvers (CVPRW'20)
• Standard setting, encoder is a deep neural network, other players are closed-form solvers.
• Local optima

Optimizing Likelihood Can be Sub-Optimal

Adversary

Encoder

Equilibrium

Maximum Entropy Adversarial Representation Learning

Encoder optimizes entropy of adversary instead of likelihood.

Adversary

Encoder

Equillibrium

Maximum Entropy ARL Continued...

• Three player game between:
• Encoder extracts features $\mathbf{z}$
• Target Predictor for desired task from features $\mathbf{z}$
• Adversary extracts sensitive information from features $\mathbf{z}$
• Three Player Non-Zero Sum Game:
\begin{equation} \begin{aligned} \min_{\mathbf{\theta}_A} & \mbox{ } \underbrace{\color{orange}{J_1(\mathbf{\theta}_E,\mathbf{\theta}_A)}}_{\color{orange}{\mbox{error of adversary}}} \\ \min_{\mathbf{\theta}_E,\mathbf{\theta}_T} & \mbox{ } \underbrace{\color{cyan}{J_2(\mathbf{\theta}_E,\mathbf{\theta}_T)}}_{\color{cyan}{\mbox{error of target}}} - \alpha \underbrace{\color{orange}{J_3(\mathbf{\theta}_E,\mathbf{\theta}_A)}}_{\color{orange}{\mbox{entropy of adversary}}} \nonumber \end{aligned} \end{equation}

Geometry of Optimization

Solution: Spectral Adversarial Representation Learning

• Lagrangian formulation:
\begin{equation} \min_{\mathbf{\Theta}_E} \Big\{(1-\lambda){\color{cyan}{J_t(\mathbf{\Theta}_E)}}- (\lambda) {\color{orange}{J_s (\mathbf{\Theta}_E)} }\Big\} \nonumber \end{equation}

B. Sadeghi, R. Yu, V.N. Boddeti, "On the Global Optima of Kernelized Adversarial Representation Learning," ICCV 2019

Closed-Form Solvers

• Encoder extracts features $\mathbf{z}$
• Target Predictor: kernel ridge regressor to predict target from $\mathbf{z}$
• Adversary: kernel ridge regressor to extract sensitive information from $\mathbf{z}$

B. Sadeghi, L. Wang, V.N. Boddeti, "Adversarial Representation Learning with Closed-Form Solutions," CVPRW 2020

Properties of Ideal Embedding

Bounds on Trade-Off

Practical Applications

Application-1: Fair Classification

• UCI Adult Dataset (creditworthiness, gender)

Fair Classification: Interpreting Encoder Weights

Embedding Weights (Adult Dataset)

Application-2: Mitigating Privacy Leakage

• CelebA Dataset (smile, gender)

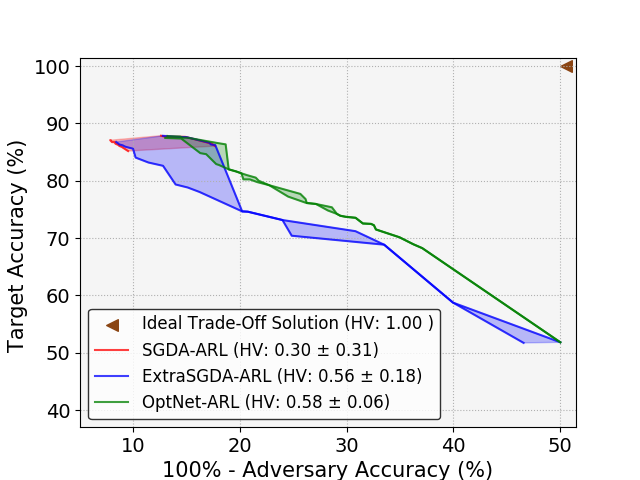
Application-3: Mitigating Privacy Leakage

Application-4: Illumination Invariance

Open Questions

• Understand fundamental trade-off between utility and fairness.
• Understand achievable trade-off between utility and fairness.
• Optimization of adversarial training, especially three player games under general settings.
• $\dots$

Summary

• Striving step towards explicit control of,
• semantic information in learned representations
• access to information in learned representations



• Many unanswered open questions and practical challenges.