HEFT: Homomorphically Encrypted Fusion of Biometric Templates
Luke Sperling$\dagger$, N. Ratha$\ddagger$, A. Ross$\dagger$, V. Boddeti$\dagger$
$\dagger$Michigan State University, $\ddagger$University at Buffalo
12th October, 2022
IJCB 2022
Motivation
Fusion of Biometric Information
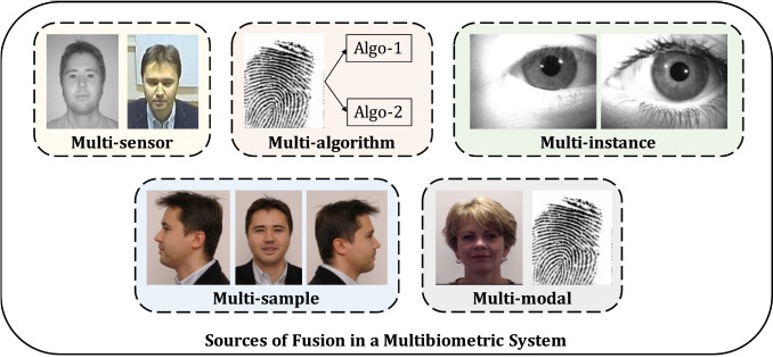
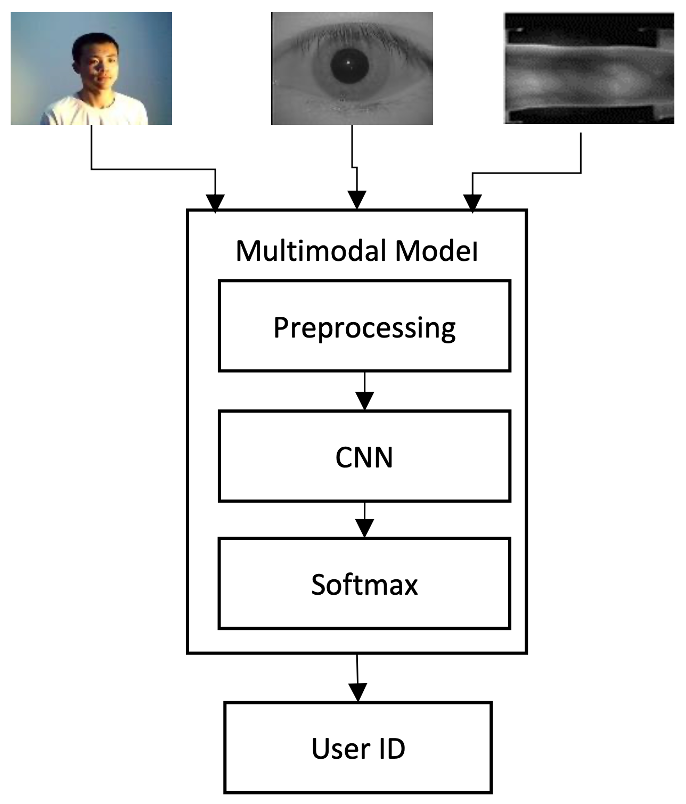
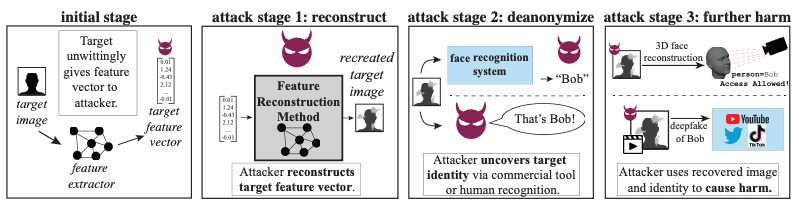
Information Leakage from Representations


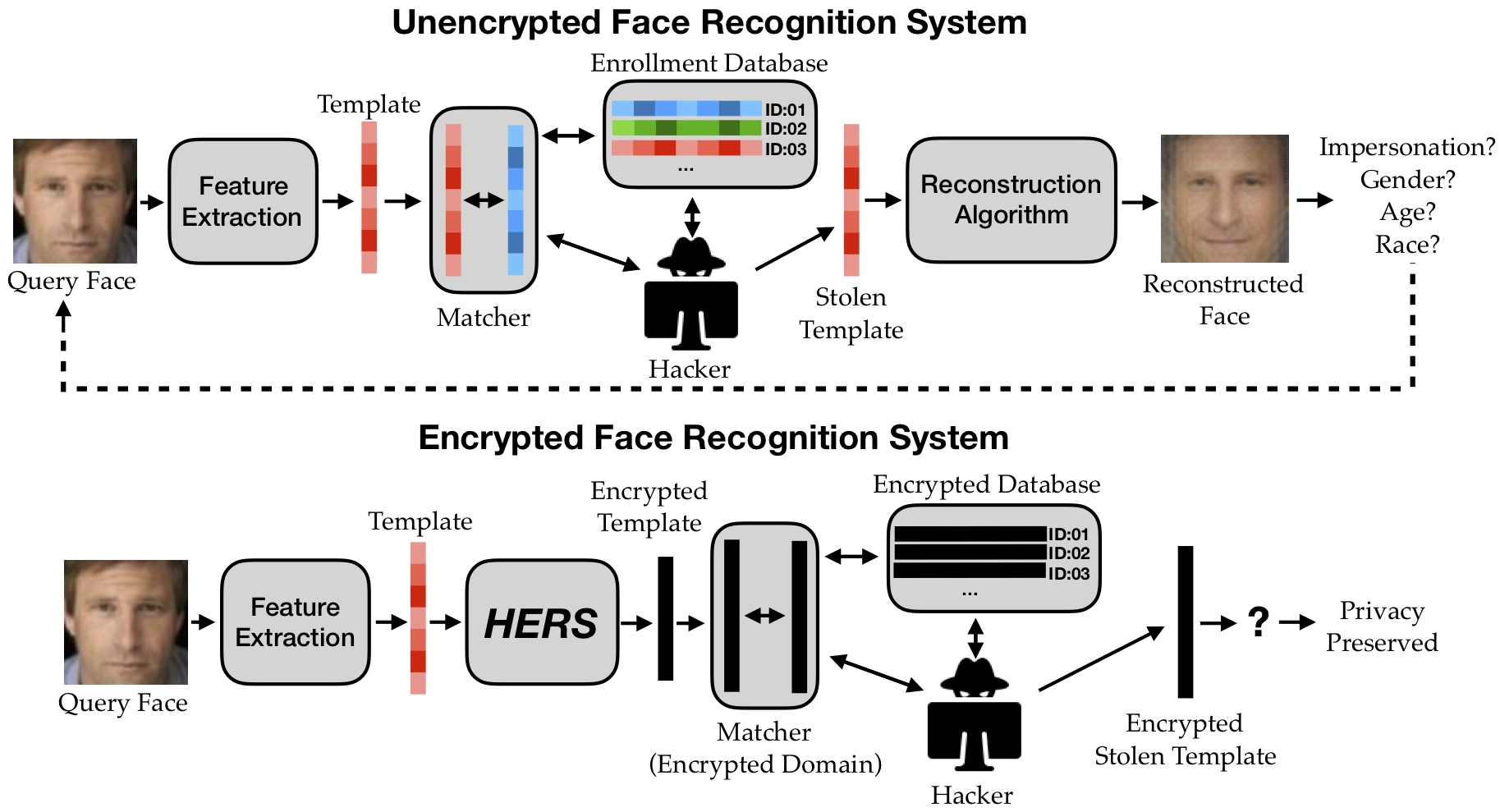
Encryption: The Holy Grail?
- Data encryption is an attractive option
- protects user's privacy
- enables free and open sharing
- mitigate legal and ethical issues
- Encryption scheme needs to allow computations directly on the encrypted data.
- Solution: Homomorphic Encryption
Key Idea of Homomorphic Encryption
Ring Learning with Errors



| op | plaintext | ciphertext |
|---|---|---|
| $x$ | $(x + e_1) \mbox{ mod } t$ | |
| $y$ | $(y + e_2) \mbox{ mod } t$ | |
| $+$ | $x+y$ | $(x+y + e_3') \mbox{ mod } t$ |
| $\times$ | $x\times y$ | $(x\times y + e_4'') \mbox{ mod } t$ |
FHE in Biometrics

- "Secure Face Matching Using Fully Homomorphic Encryption,", BTAS 2018
- "HERS: Homomorphically Encrypted Representation Search,", TBIOM 2022
-
- Focussed on protecting database of templates.
- Allows match score computation in the encrypted domain.
HEFT
HEFT: Overview

HEFT: Concatenation

Homomorphic Concatenation

HEFT: Linear Projection

Linear Projection



Linear Projection Comparison
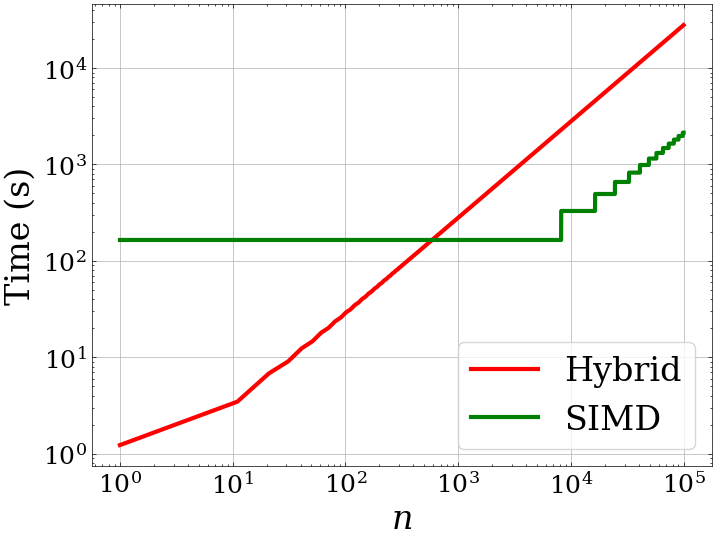
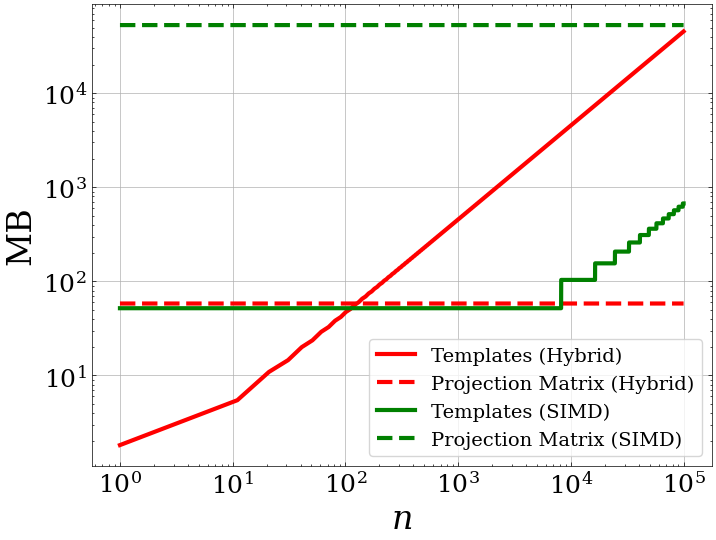
- Hybrid
- Pros: Low memory and runtime overhead
- Cons: Scales linearly with number of samples
- SIMD
- Pros: Scales well with number of samples
- Cons: High memory and runtime overhead
HEFT: Feature Normalization

$\ell_2$-Normalization of Vector
where
- $\dagger$: problematic operations for FHE
Inverse Square Root: Polynomial Approximation
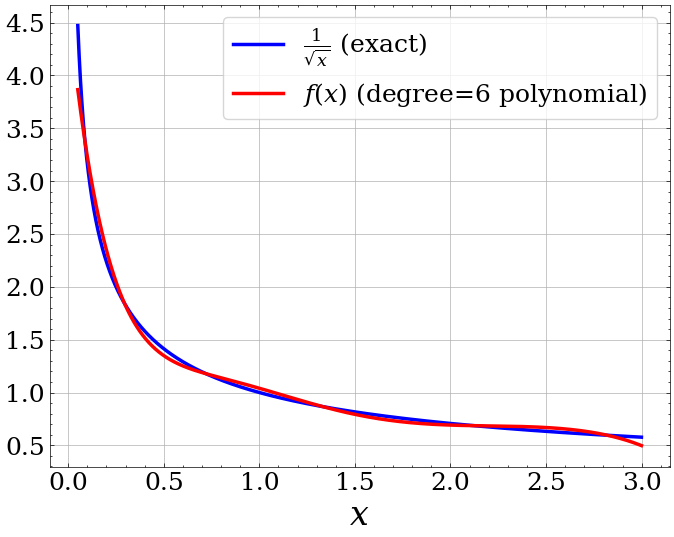
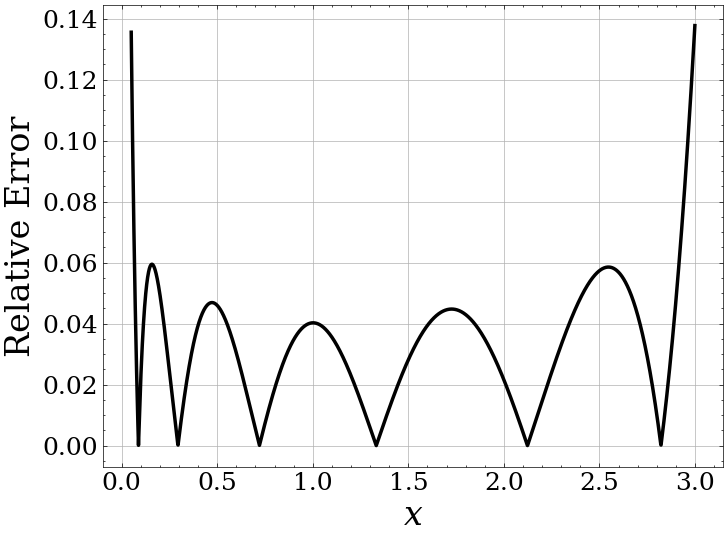
FHE-Aware Learning
- FHE is limited to specific operations on encrypted data.
- Normalization is not directly computable - need to approximate.
- Approximation is a source of error and hence a loss of matching performance
- We incorporate approximate normalization into our training of the projection matrix to recover performance
Loss Function
- $$Loss = \lambda \underbrace{\frac{\sum_M d(\mathbf{c}_i, \mathbf{c}_j)}{|M|}}_{ \color{orange}{Pull} } + (1-\lambda)\underbrace{\frac{\sum_{V}[m + d(\mathbf{c}_i, \mathbf{c}_j) - d(\mathbf{c}_i, \mathbf{c}_k)]_{+}}{|V|}}_{ \color{orange}{Push} }$$
- where $$d(\mathbf{c}_i, \mathbf{c}_j) = 1-P\underbrace{f(\mathbf{c}_i)}_{ \color{cyan}{approximation} } \cdot P\underbrace{f(\mathbf{c}_j)}_{ \color{cyan}{approximation} }$$ $f(\cdot)$ approximates the inverse norm of a vector.
Numerical Evaluation
Experimental Setup

- Synthetic fusion dataset by randomly pairing classes.
- 10,760 samples over 188 classes.
Fusion Improves Performance, Reduces Dimensionality
- Fusion improves performance:
- Face by 11.07%
- Voice by 9.58%
- Dimensionality Reduction: $512D \rightarrow 32D$ (16$\times$ compression)
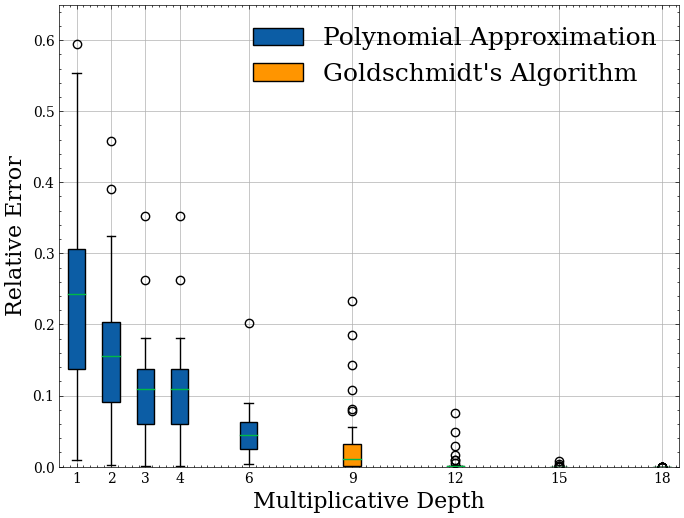
Comparison of Normalization Methods
Computational Complexity
- Projection is costliest operation
- Projection is costliest operation
Summary

- Introduces the first multimodal feature-level fusion system in the encrypted domain.
- Improves performance of original templates while reducing their dimensionality.
- Incorporates polynomial approximation for approximate normalization.
- Incorporates FHE-Aware Learning to improve performance.