HERS: Homomorphically Encrypted Representation Search
Joshua Engelsma, Anil Jain, Vishnu Naresh Boddeti
Michigan State University
IJCB 2022 (Published at TBIOM 2022)
Embeddings in Biometrics
- Learned Embeddings:


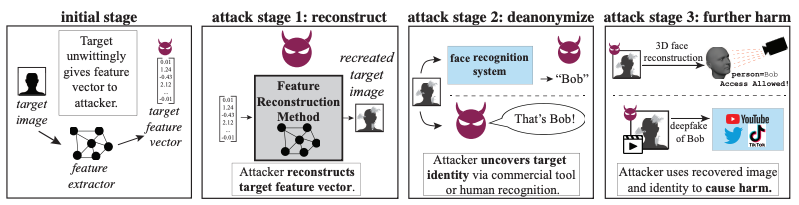
Privacy Attacks from Representations

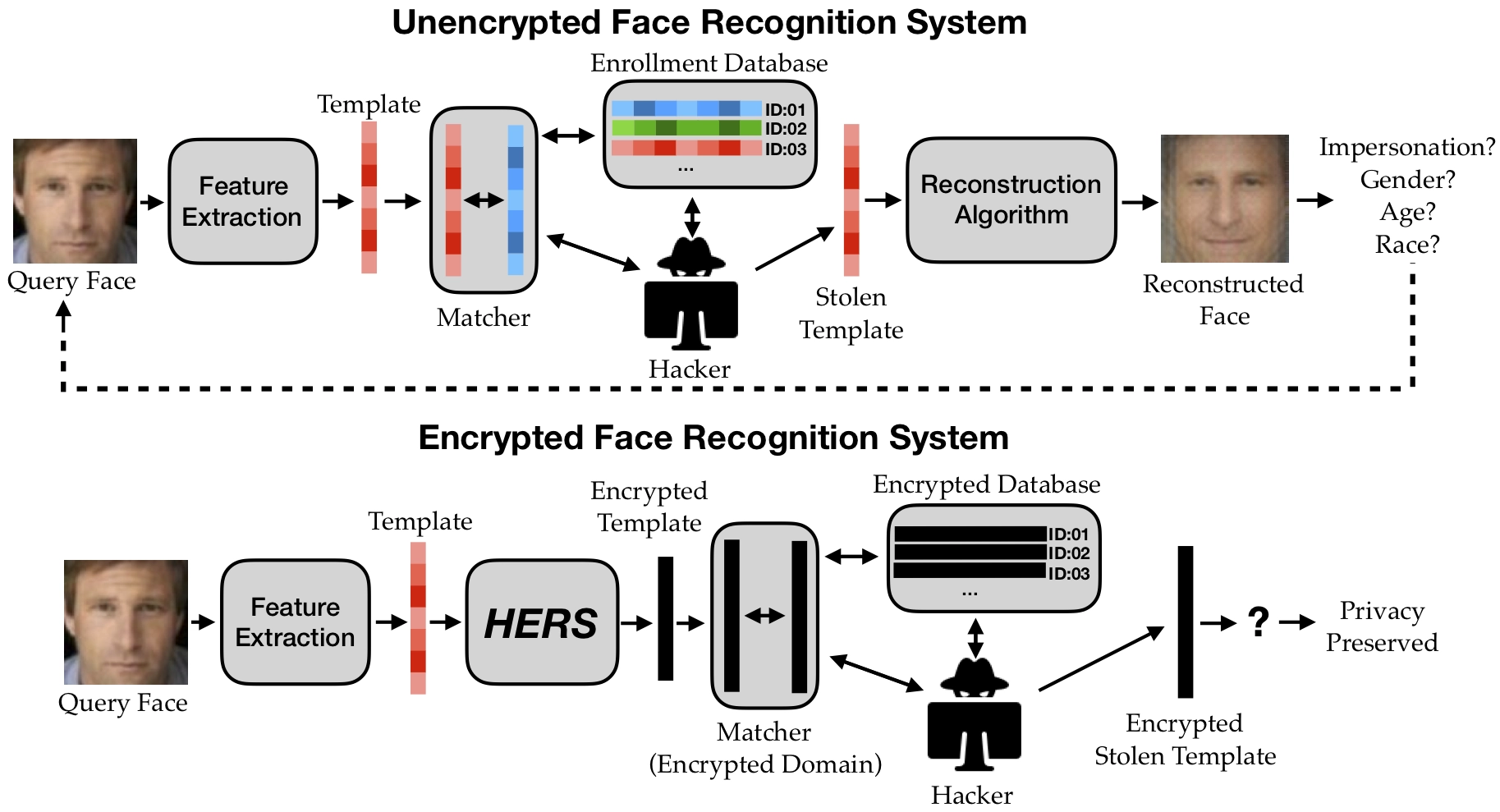
Encryption: The Holy Grail?
- Data encryption is an attractive option
- protects user's privacy
- enables free and open sharing
- mitigate legal and ethical issues
- Encryption scheme needs to allow computations directly on the encrypted data.
- Solution: Homomorphic Encryption
Key Idea of Homomorphic Encryption
RLWE: Ring Learning with Errors



| op | plaintext | ciphertext |
|---|---|---|
| $x$ | $(x + e_1) \mbox{ mod } t$ | |
| $y$ | $(y + e_2) \mbox{ mod } t$ | |
| $+$ | $x+y$ | $(x+y + e_3') \mbox{ mod } t$ |
| $\times$ | $x\times y$ | $(x\times y + e_4'') \mbox{ mod } t$ |
Overview
Homomorphic Inner Products
- Feature Matching: \begin{eqnarray} \mbox{Euclidean Distance: } d(\mathbf{x},\mathbf{y}) &=& \|\mathbf{x}-\mathbf{y}\|^2_2 = \mathbf{x}^T\mathbf{x} + \mathbf{y}^T\mathbf{y} - 2\mathbf{x}^T\mathbf{y} \nonumber \\ \mbox{Cosine Similarity: } s(\mathbf{x},\mathbf{y}) &=& \frac{\mathbf{x}^T\mathbf{y}}{\|\mathbf{x}\|\|\mathbf{y}\|} \nonumber \end{eqnarray}
- Inner Product: \[\mathbf{x}^T\mathbf{y}=\sum_{i=1}^d x_iy_i\]
- Homomorphic Inner Product: \[s(\mathbf{x},\mathbf{y}) = \mathcal{D}\left(\sum_{i=1}^d \mathcal{E}(x_i, \mathbf{\theta}_e)\mathcal{E}(y_i, \mathbf{\theta}_e), \mathbf{\theta}_d\right)\]
Prior Work

- Vishnu Naresh Boddeti, "Secure Face Matching Using Fully Homomorphic Encryption," BTAS 2018
Main Limitation

- Encrypts one vector at a time.
- Computation scales linearly with gallery size $n$.
- 38.4 hours to match a query.
- 9TB storage for gallery.
- Vishnu Naresh Boddeti, "Secure Face Matching Using Fully Homomorphic Encryption," BTAS 2018
Scalable Score Computation in FHE
- Dimensionality Reduction (Machine Learning)
- Scalable Data Encoding (FHE)
Data Encoding for Scalable Search

- Encrypts one dimension at a time.
- Computation scales linearly with dimension $d$.
- 25 minutes (from 38.4 hours) to match a query.
- 280 GB storage (from 9TB) for gallery.
Efficient Search with Dimensionality Reduction

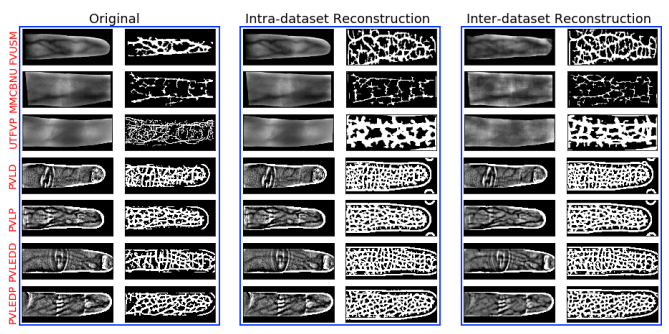
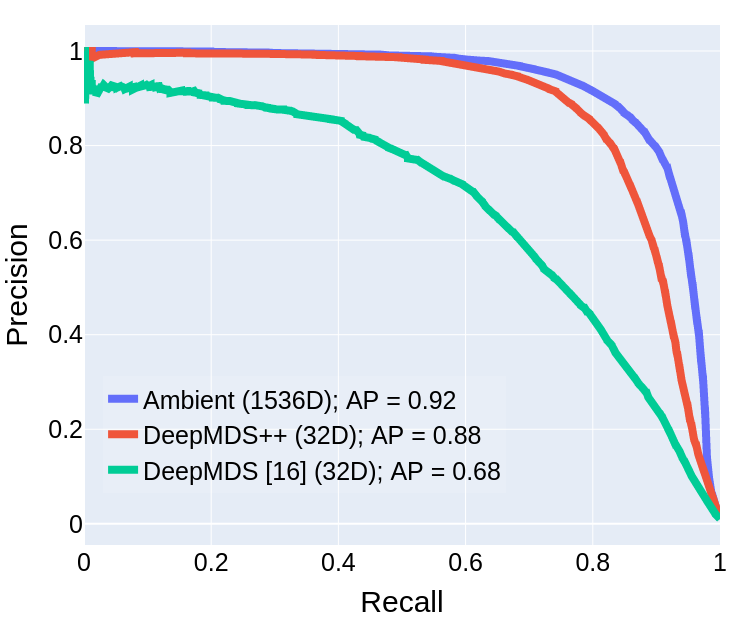
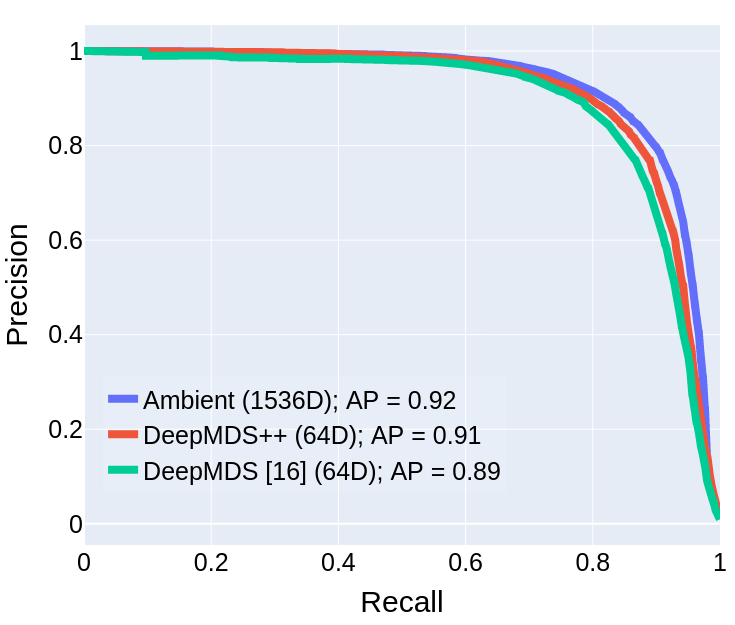
- Build upon DeepMDS for dimensionality reduction.

- Sixue Gong, Vishnu Boddeti, Anil Jain, "On the Intrinsic Dimensionality of Image Representations,", CVPR 2019
DeepMDS++
- DeepMDS Loss:
- $\mathcal{L}_D = \frac{1}{b_1}\|\mathbf{D}_G - \mathbf{\hat{D}}_G\|_F^2 + \frac{1}{b_2}\|\mathbf{D}_I - \mathbf{\hat{D}}_I\|_F^2$
- Additional Ideas:
- Covariance Penalty $\mathcal{L}_c = \|\mathbf{C} - diag(\mathbf{C})\|_F^2$
- Hard Negative Mining $P_G = argsort(\mathbf{D}_G - \mathbf{\hat{D}}_G) \quad P_I = argsort(\mathbf{D}_I - \mathbf{\hat{D}}_I)$
Experimental Setup

- Datasets: ImageNet-100K, MegaFace-1M, Fingerprint-100M
- Models: ResNet, ArcFace, DeepPrint
Computational Complexity

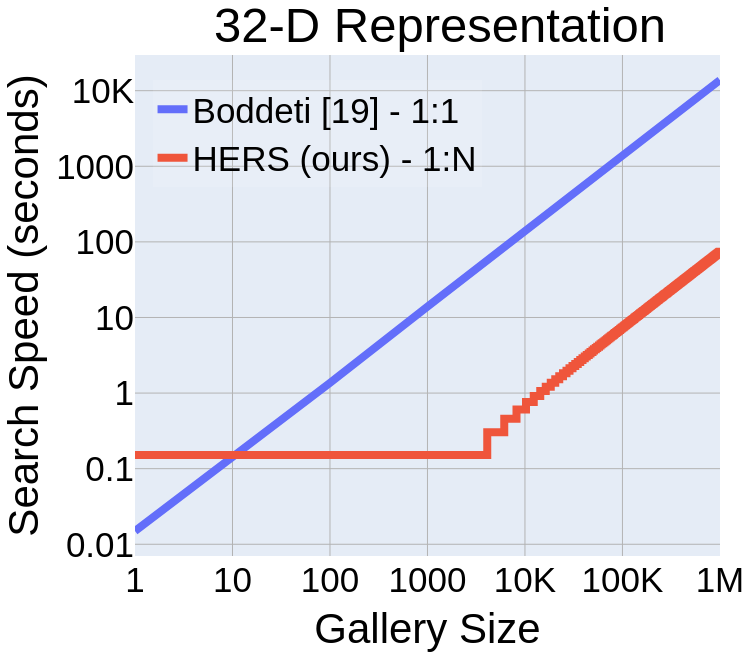
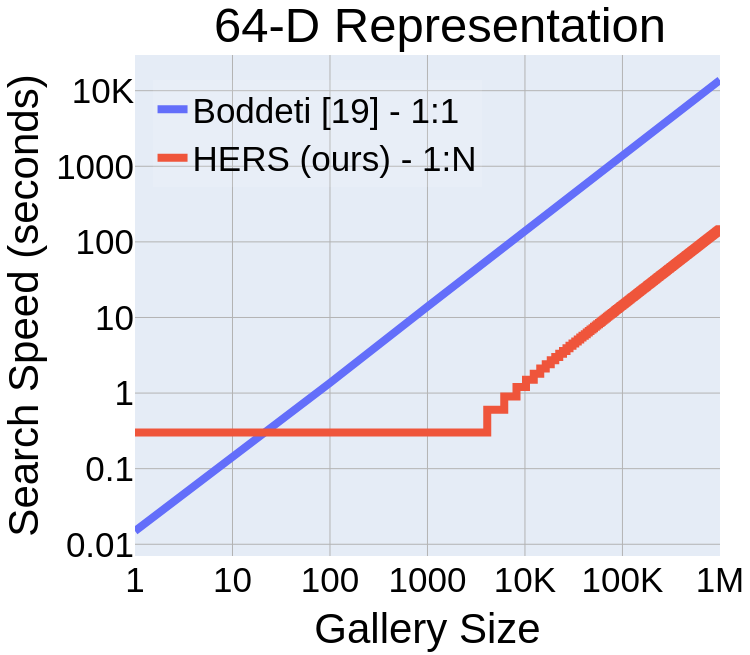
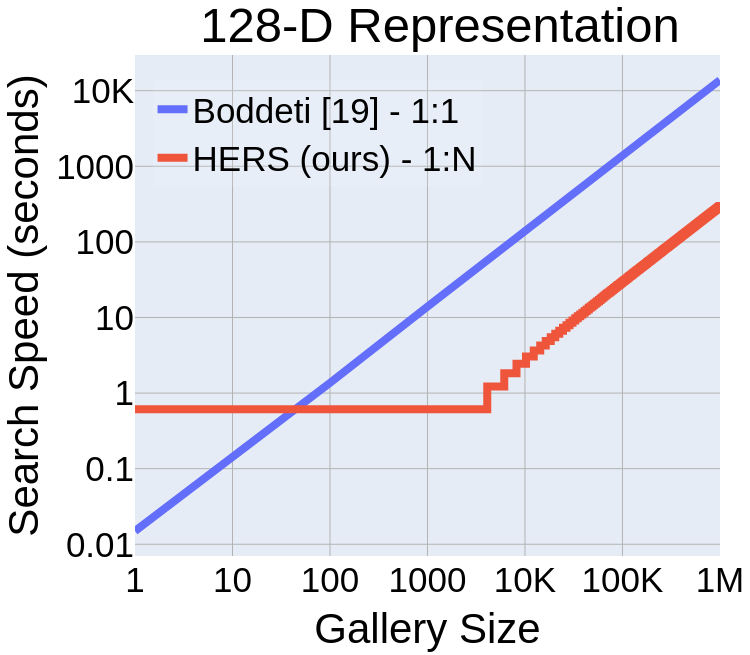
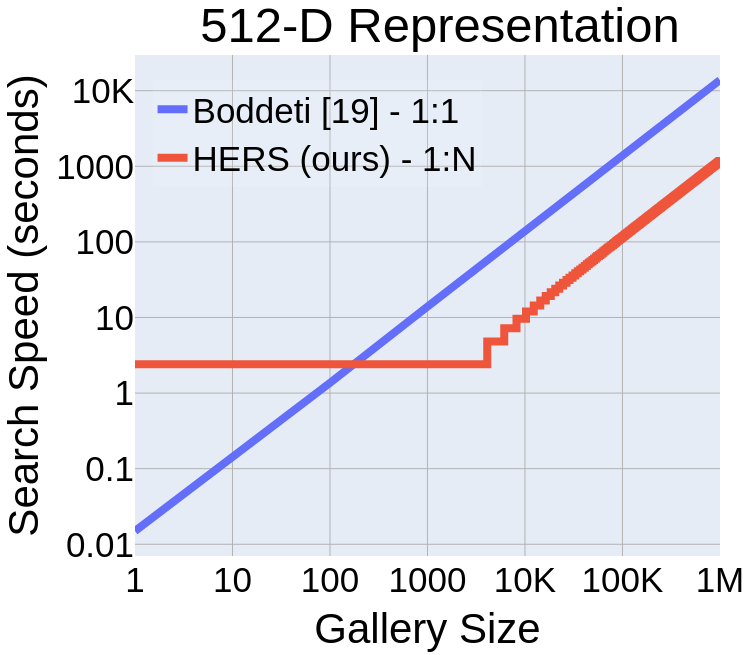
Scaling to 100 Million Gallery
Biometric Search (Rank-1 Accuracy)
Effectiveness of DeepMDS++
Image Retrieval on ImageNet
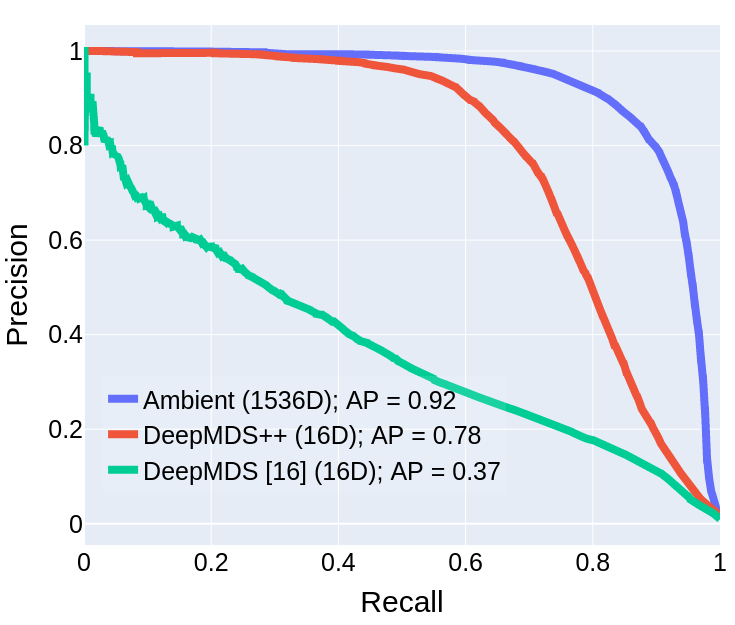
Two-Stage Search
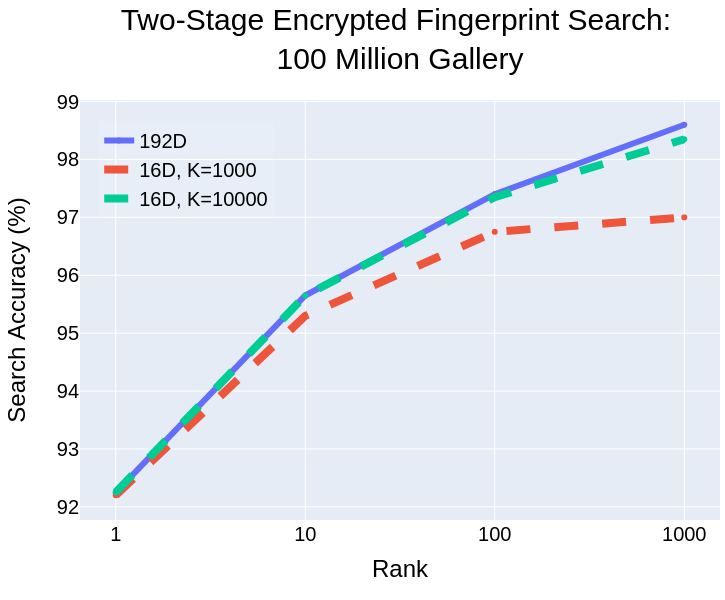
- Use compressed features (16D) to perform approximate search.
- Narrow down search to $K$, say 10000, nearest neighbors.
- Use original features (192D) to perform exact search over $K$.
- 9$\times$ speed-up (4500 sec to 500 sec) without loss of accuracy.
Summary

- Scalable biometric matching over homomorphically encrypted templates.
- Key Ideas: Dimensionality Reduction and SIMD Encoding.
- Demonstrated biometric search against a 100 Million encrypted gallery under 500 secs.
