Homomorphically Encrypted Biometric Template Fusion

Vishnu Boddeti

Michigan State University

8th March, 2023

Norwegian Biometrics Laboratory Workshop

Vulnerabilities in Biometrics

Biometric systems suffer from vulnerabilities.

Mitigating Security Vulnerabilities

Biometrics + Encryption

Encrypted Biometrics

Data encryption is an attractive option

protects user's data from unauthorized access
protects service provider's models from unauthorized access
facilitates free and open sharing of private data
mitigate legal and ethical issues

Traditional solutions need data decryption for computation.
Security only during data transmission.

Homomorphic Encryption: The Holy Grail?

Cryptographic scheme needs to allow computations directly on the encrypted data.

Solution: Homomorphic Encryption
Attractive Property: Conjectured to be post-quantum secure for appropriate choice of encryption parameters.

Limitations: only supports additions and multiplications.

Template Security with Homomorphic Encryption

Biometric Features

Learned Features:

Enrollment

Authentication

Information Leakage from Representations

Attacks on Face templates

"Assessing Privacy Risks from Feature Vector Reconstruction Attacks," arXiv:2202.05760

Face reconstruction from template

"On the reconstruction of face images from deep face templates," TPAMI, 2018

Finger vein reconstruction from binary templates

"Inverse Biometrics: Reconstructing Grayscale Finger Vein Images from Binary Features," IJCB, 2020

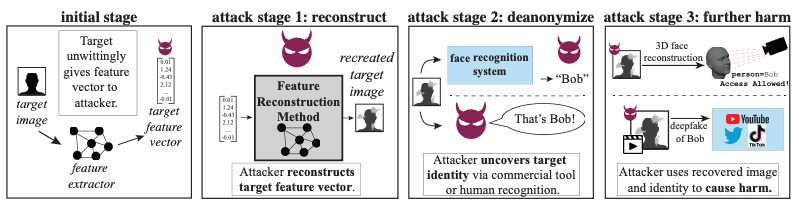
Existing Applications of FHE for Biometric Security

Template protection using Homomorphic Encryption:

Encrypt database of features.
Encrypt query feature.
Match score computed directly in encrypted domain.

Prior Work: Template Protection with Homomorphic Encryption

Boddeti, "Secure Face Matching Using Fully Homomorphic Encryption," BTAS 2018

Bassit et.al, "Multiplication-Free Biometric Recognition for Faster Processing under Encryption," IJCB 2022

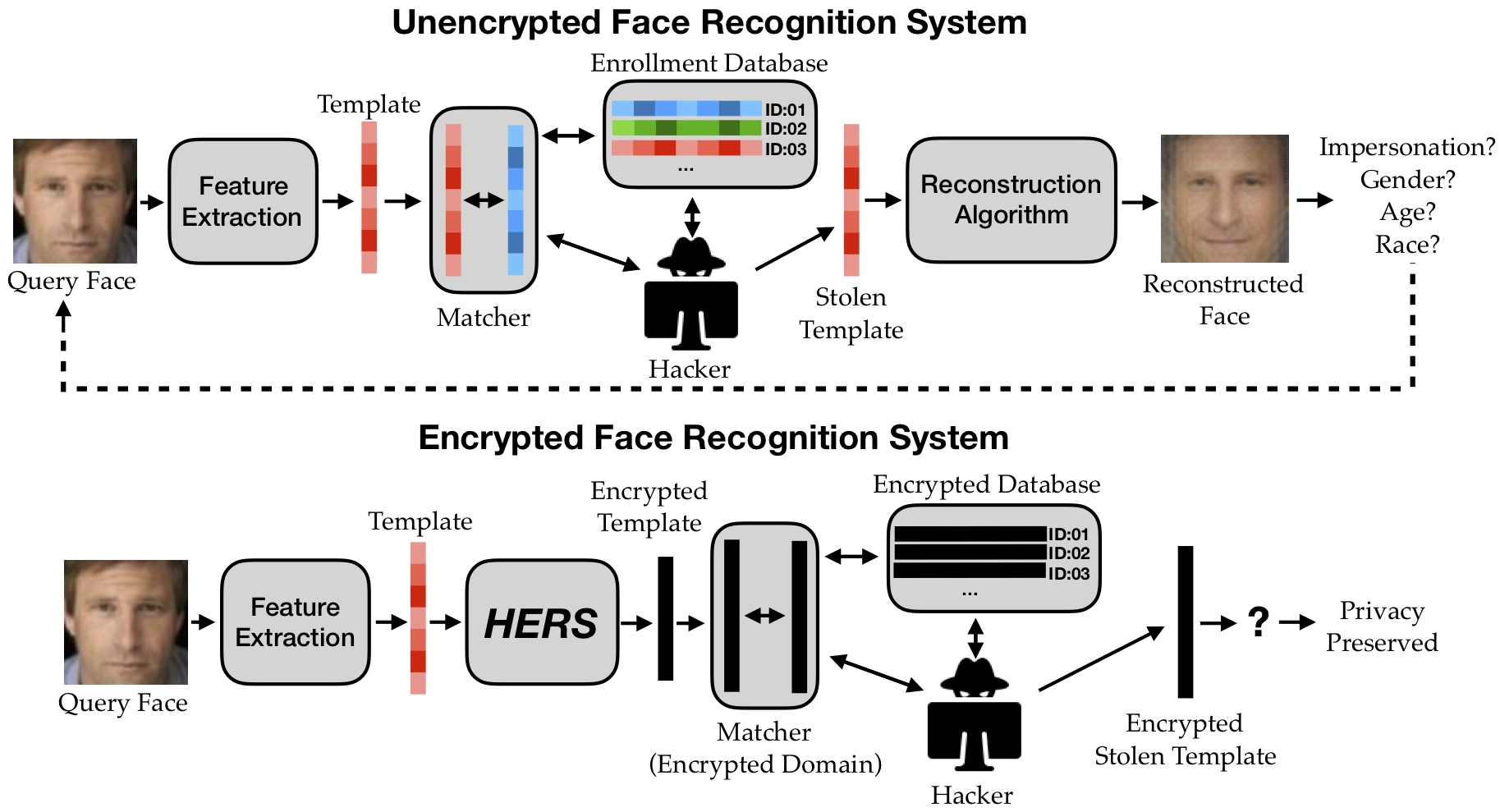
Engelsma, Jain, Boddeti, "HERS: Homomorphically Encrypted Representation Search," TBIOM 2022

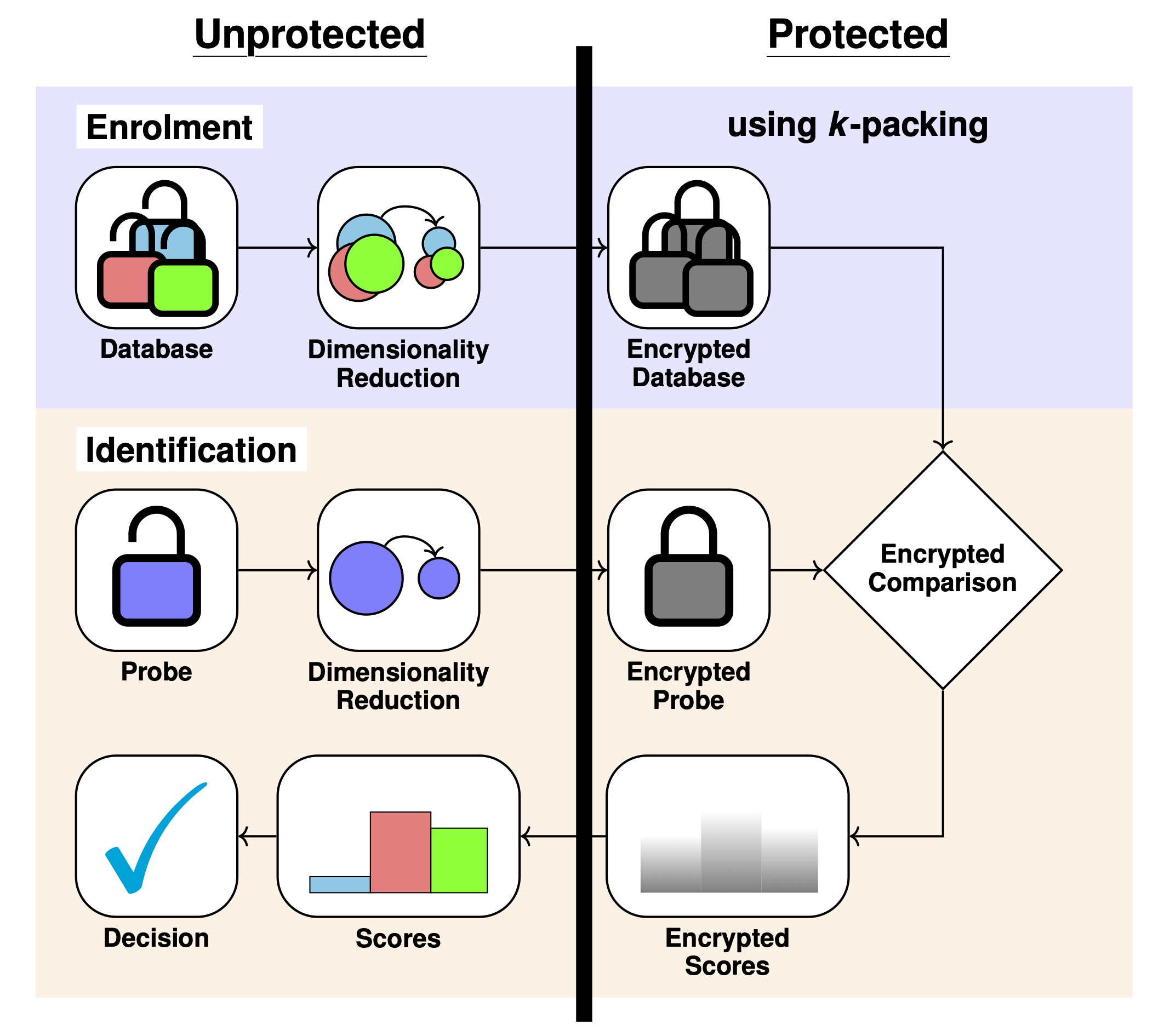
Bauspieß et.al, "Improved Homomorphically Encrypted Biometric Identification Using Coefficient Packing," IWBF 2022

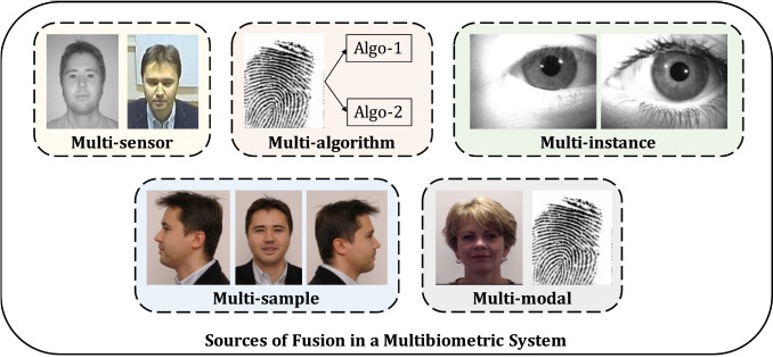
Secure Biometric Template Fusion

Fusion of Biometric Information

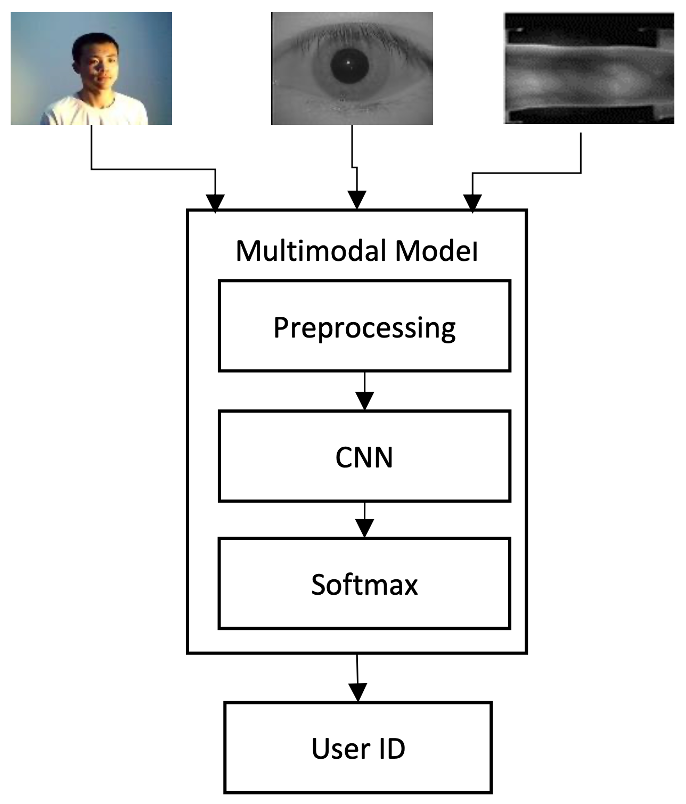
"A comprehensive overview of biometric fusion."Information Fusion, 2019"

"Deep learning approach for multimodal biometric recognition system based on fusion of iris, face, and finger vein traits." Sensors, 2020

HEFT: Overview

Sperling et al., "HEFT: Homomorphically Encrypted Fusion of Biometric Templates," IJCB 2022 (Best Student Paper Award)

HEFT: Concatenation

Homomorphic Concatenation

HEFT: Linear Projection

Linear Projection

$z = P \times \begin{bmatrix}\mathbf{x}_1 \\ \mathbf{x}_2\end{bmatrix}$

Naive

Hybrid

SIMD

Linear Projection Comparison

Computational Complexity

Space Complexity

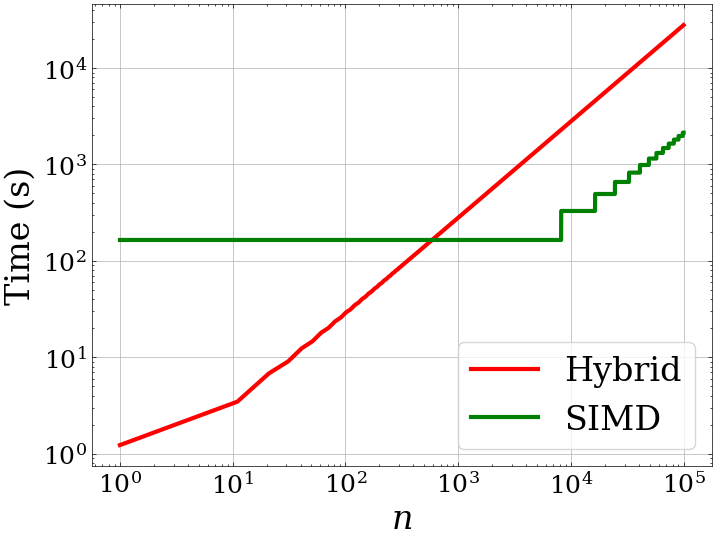
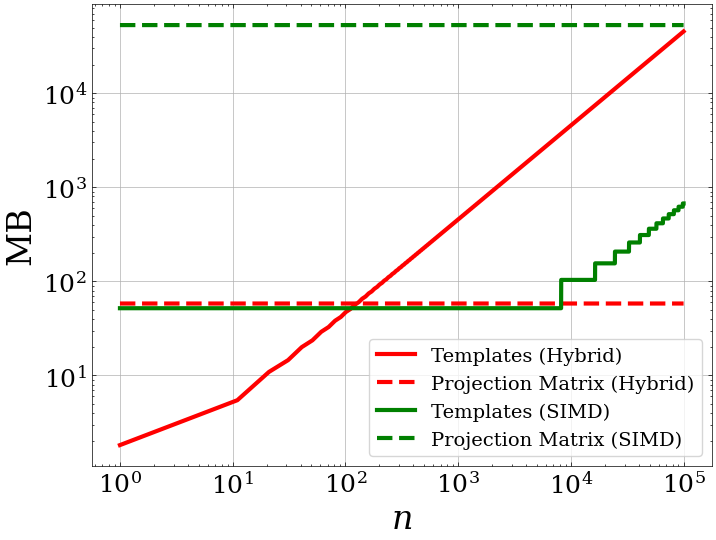
Hybrid

Pros: Low memory and runtime overhead
Cons: Scales linearly with number of samples

SIMD

Pros: Scales well with number of samples
Cons: High memory and runtime overhead

HEFT: Feature Normalization

$\ell_2$-Normalization of Vector

$\hat{\mathbf{u}} = \frac{\mathbf{u}}{\|\mathbf{u}\|_2} \quad \rightarrow \quad$ division^$\dagger$

where

$\|\mathbf{u}\|_2 = \sqrt{\sum_{i=1}^d u_i^2} \quad \rightarrow \quad$ square-root^$\dagger$

^$\dagger$: problematic operations for FHE

Inverse Square Root: Polynomial Approximation

$$\frac{1}{\sqrt{x}} = \sum_{i=1}^6 a_i x^i$$

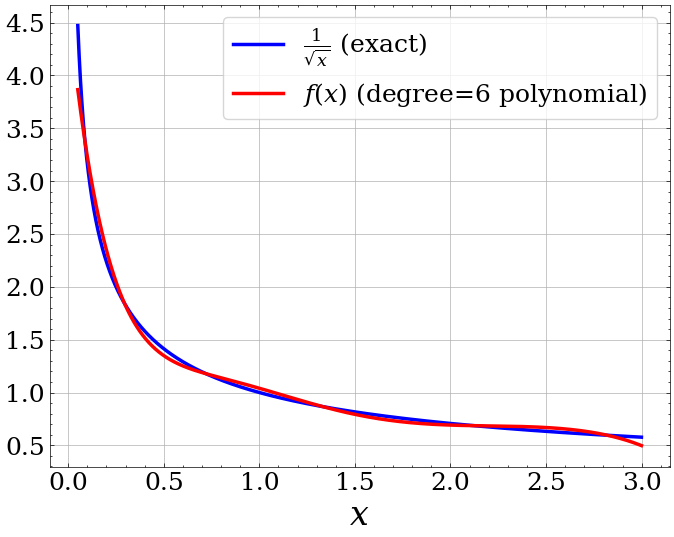
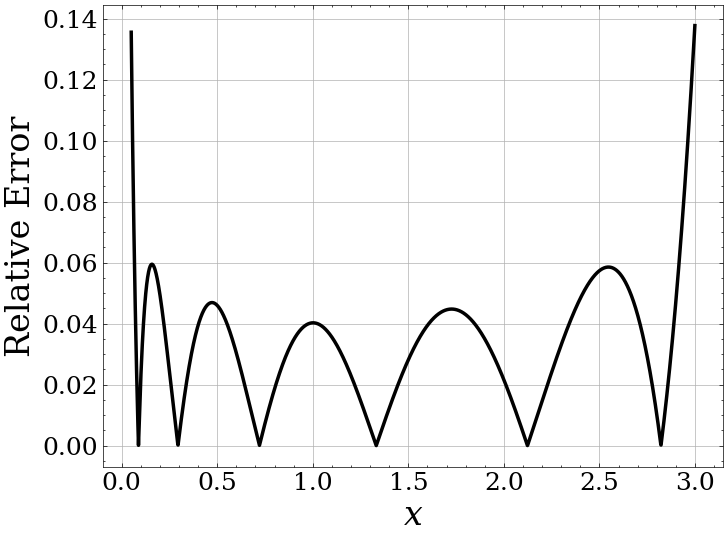
FHE-Aware Learning

Account for the limitations of FHE to improve performance

FHE is limited to specific operations on encrypted data.

Normalization is not directly computable - need to approximate.

Approximation is a source of error and hence a loss of matching performance

We incorporate approximate normalization into our training of the projection matrix to recover performance

Loss Function

Main Idea: FHE-Aware Learning

$$Loss = \lambda \underbrace{\frac{\sum_M d(\mathbf{c}_i, \mathbf{c}_j)}{|M|}}_{ \color{orange}{Pull} } + (1-\lambda)\underbrace{\frac{\sum_{V}[m + d(\mathbf{c}_i, \mathbf{c}_j) - d(\mathbf{c}_i, \mathbf{c}_k)]_{+}}{|V|}}_{ \color{orange}{Push} }$$
where $$d(\mathbf{c}_i, \mathbf{c}_j) = 1-P\underbrace{f(\mathbf{c}_i)}_{ \color{cyan}{approximation} } \cdot P\underbrace{f(\mathbf{c}_j)}_{ \color{cyan}{approximation} }$$ $f(\cdot)$ approximates the inverse norm of a vector.

Numerical Evaluation

Experimental Setup

Cross-Posed Labelled Faces in the Wild

Down

Dog

Bird

Backward

Google Speech Commands

Synthetic fusion dataset by randomly pairing classes.
10,760 samples over 188 classes.

Encryption and Training Parameters

Encryption Parameters: $(n,q)$

Library: Microsoft SEAL
$n$: $2^{14}$ or $2^{15}$ depending on multiplicative depth.
$q$: chain of large prime numbers totaling 420, 580 or 860 bits.

Training Parameters:

Learning Rate: $5 \times 10^{-3}$
Weight Decay: $1 \times 10^{-4}$
Training Epochs: 1000

Fusion Improves Performance, Reduces Dimensionality

Fusion improves performance:
- Face by 11.07%
- Voice by 9.58%

Dimensionality Reduction: $512D \rightarrow 32D$ (16$\times$ compression)

Comparison of Normalization Methods

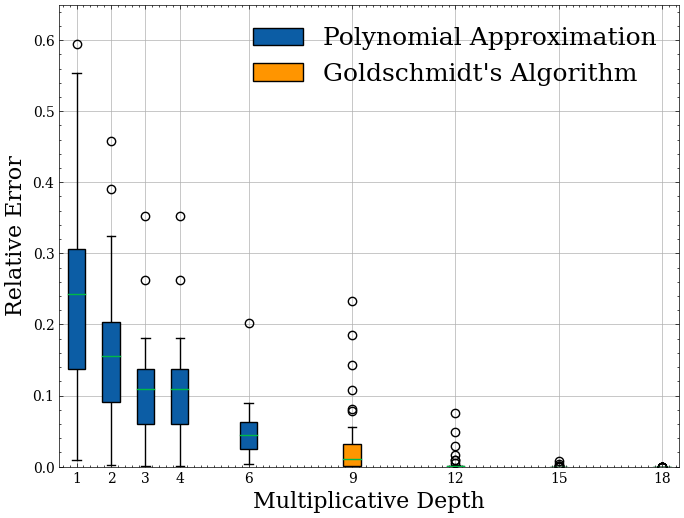
Computational Complexity

Projection is costliest operation

Projection is costliest operation

Is FHE the Panacea for Privacy?

Security and privacy are very often conflated with each other.

Different but related concepts.
Homomorphic encryption: controls access to private information.
Differential Privacy: analysis + manipulation of private information.

Postulates:

There is no privacy without security.
Homomorphic encryption is an ideal tool for enhancing privacy but it is not a privacy technique in and of itself.

Ideal solution: Differential privacy + Homomorphic Encryption

Summary

Introduces the first multimodal feature-level fusion system in the encrypted domain.
Improves performance of original templates while reducing their dimensionality.
Incorporates polynomial approximation for approximate normalization.
Incorporates FHE-Aware Learning to improve performance.

HEFT: Encrypted Biometric Fusion VishnuBoddeti