Privacy-Preserving Computer Vision with Homomorphic Encryption
Stanley Black and Decker Seminar
Vishnu Boddeti
June 3, 2021
Computer Vision Today






Key Driver
Dark Data
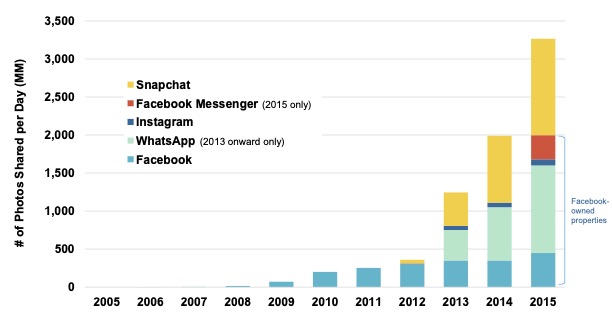
- About 3.5 billion photos are shared publicly.
- Conservatively, $2\times$-$3\times$ are not shared publicly.
- Sensitive data: medical images, surveillance images.
- Private learning:
- enables free and open sharing
- build better computer vision models

Why Privacy in Computer Vision

...consent should be given for all purposes...

Jan. 18, 2020

Misleading Claims
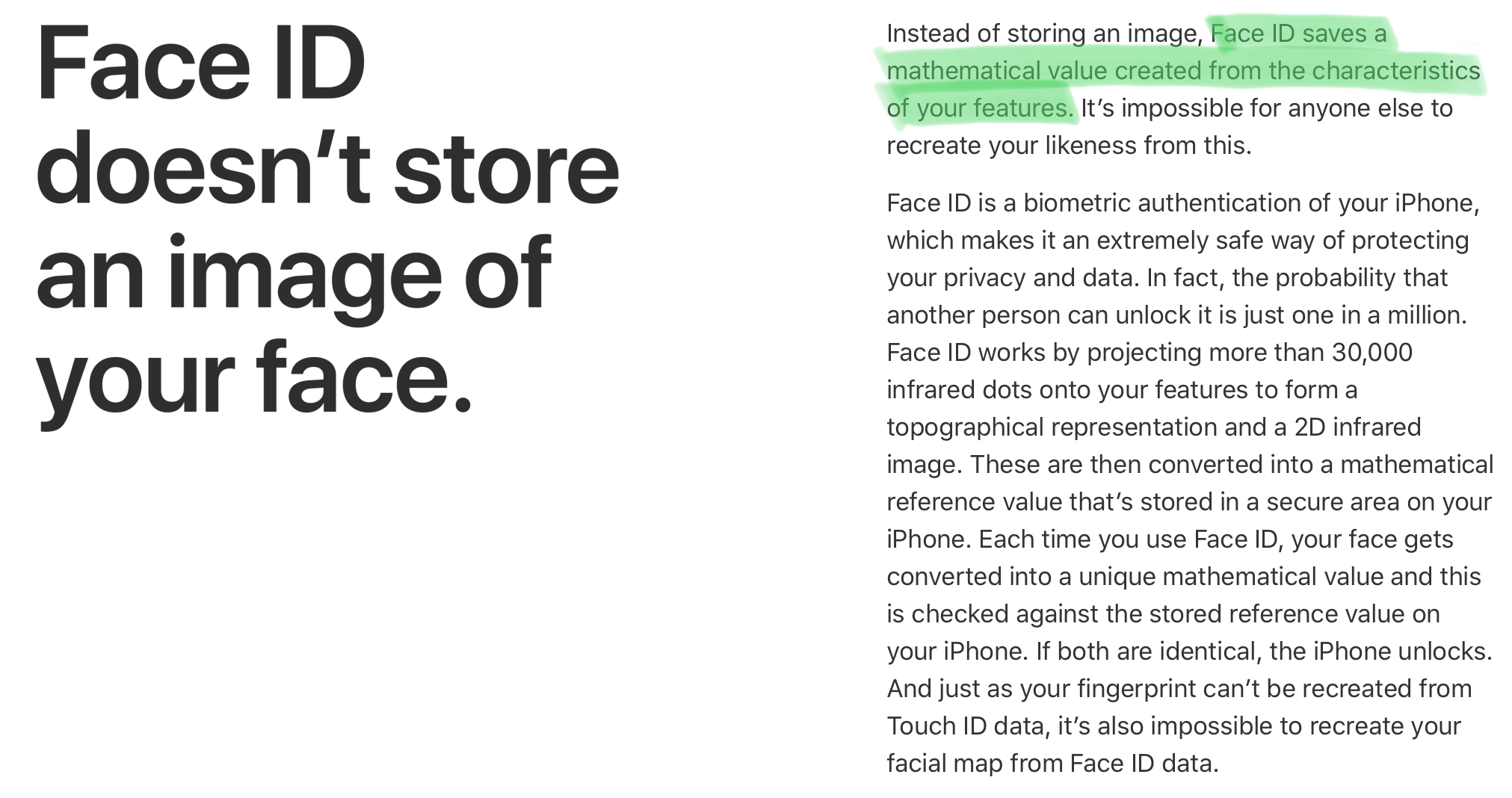
Encryption: The Holy Grail?
- Data encryption is an attractive option
- protects user's privacy
- enables free and open sharing
- mitigate legal and ethical issues
- Encryption scheme needs to allow computations directly on the encrypted data.
- Solution: Homomorphic Encrpytion
What is Homomorphic Encryption?
- Encryption that allows computations on ciphertext.
- Partially Homomorphic Encryption: allows homomorphic additions or multiplications
- Somewhat Homomorphic Encryption: allows limited number of homomorphic additions and multiplications
- Fully Homomorphic Encryption: additions and multiplications
Key Idea of Homomorphic Encryption
Ring Learning with Errors



| op | plaintext | ciphertext |
|---|---|---|
| $x$ | $(x + e_1) \mbox{ mod } t$ | |
| $y$ | $(y + e_2) \mbox{ mod } t$ | |
| $+$ | $x+y$ | $(x+y + e_3') \mbox{ mod } t$ |
| $\times$ | $x\times y$ | $(x\times y + e_4'') \mbox{ mod } t$ |
Machine Learning and Homomorphic Encryption
- Main Challenges:
- Homomorphic Encryption:
- Supports only basic arithmetic operations (additions, subtractions, multiplications and divisions)
- Each basic operation is computationally expensive.
- Machine Learning:
- Requires complex mathematical operations, including non-linear operations.
- Computationally challenging in it's own right (big-data, large models).
Today's Agenda
- Leverage the advantages of ML and HE while overcoming their challenges.
- Redesign ML algorithms with constraints of HE in mind.
- Privacy-Preserving Visual Learning Using Doubly Permuted Homomorphic Encryption, ICCV 2017
- Redesign HE algorithms with constraints of ML in mind.
- Secure Face Matching Using Fully Homomorphic Encryption, BTAS 2018
- HERS: Homomorphically Encrypted Representation Search, Arxiv 2020
Federated Learning with Homomorphic Encryption
Learning from Private Data: Federated Learning
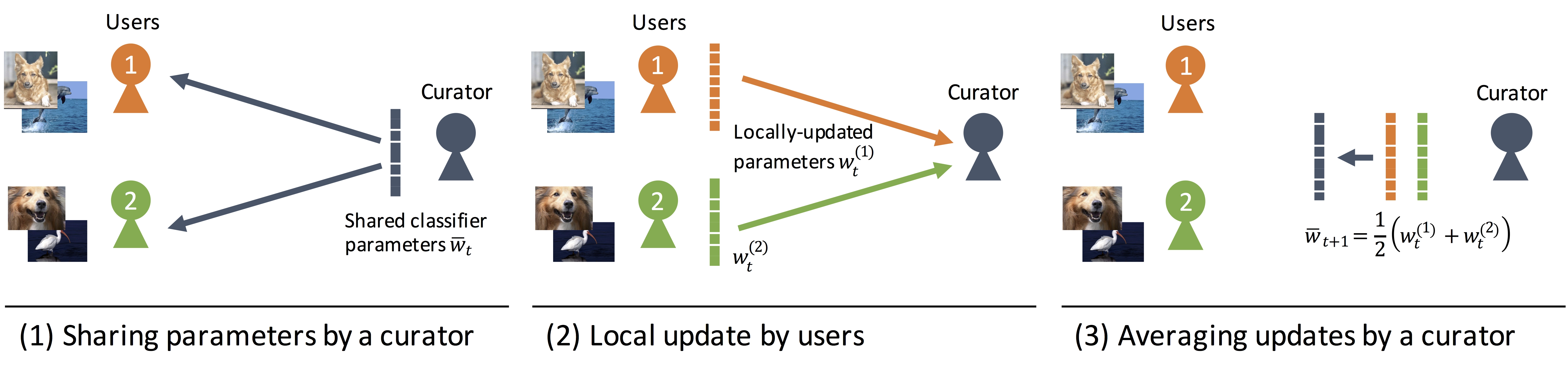
- Distributed learning of parameters from private data.
- Clients download current global model $\bar{\mathbf{w}_t}$.
- Client updates model from local data.
- Aggregator updates global model
- Yonetani et. al., "Privacy-Preserving Visual Learning Using Doubly Permuted Homomorphic Encryption", ICCV 2017
Information Leakage from Gradients
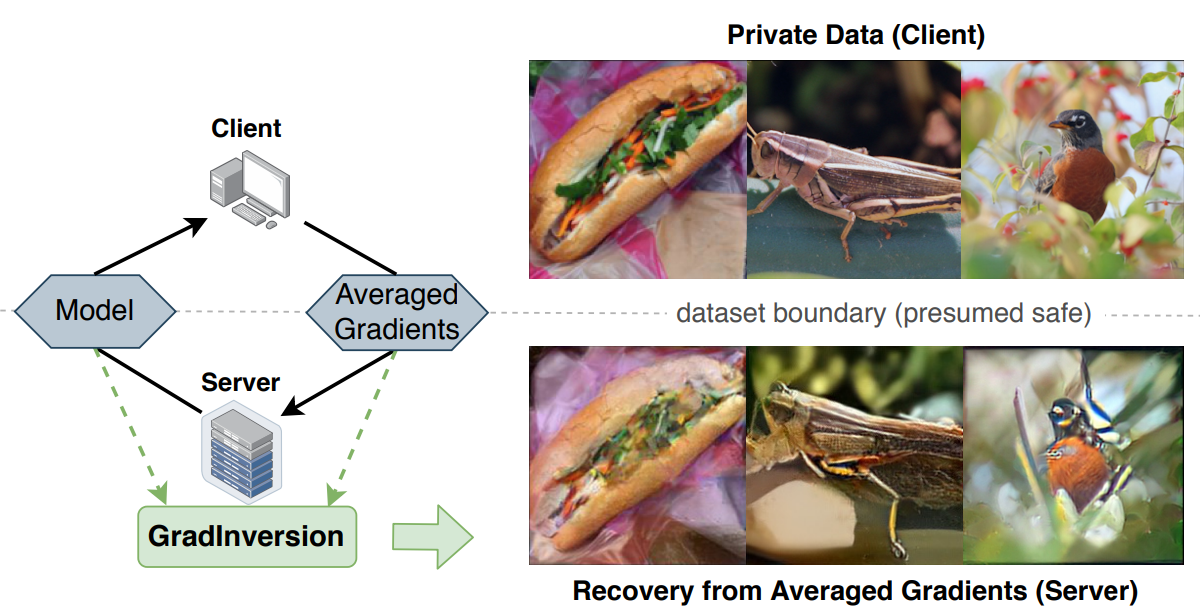
Private Learning: Differentially Private SGD

- Differential Privacy [Dwork et.al. 2006]
- Add noise to gradients to prevent reconstruction.
- Limitation: Trade-off accuracy for privacy
Private Learning: Homomorphic Encryption
- Paillier Encryption: only allows addition of integers
- Encryption Key $m$
- Base $g$
- random $r \in \{0,\dots,m-1\}$
- Ciphertext of $x$: $\xi(x) = g^xr^m \mod m^2$
- Addition, $x_1 + x_2$, in the encrypted domain. \begin{eqnarray} \xi(x_1)\xi(x_2) &=& (g^{x_1}r_1^m)(g^{x_2}r_2^m)\mod m^2 \nonumber \\ &=& g^{x_1+x_2}(r_1r_2)^m \mod m^2 \nonumber \\ &=& \xi(x_1+x_2) \nonumber \end{eqnarray}
Encrypted Federated Learning
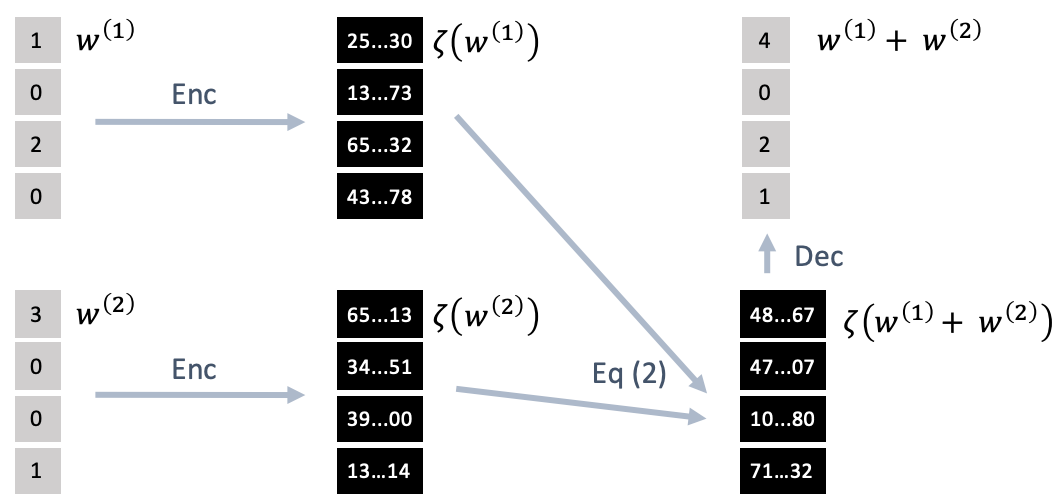
- Yonetani et. al., "Privacy-Preserving Visual Learning Using Doubly Permuted Homomorphic Encryption", ICCV 2017
Homomorphic Encryption for Sparse Data
- Sparse Data $\mathbf{x} \in \mathbb{R}^d$: $\mathbf{x} = \mathbf{K}\mathbf{v}$
- $m$: number of non-zero elements
- $\mathbf{v} \in \mathbb{R}^m$: real non-zero values
- $\mathbf{K} \in \{0,1\}^{d \times m}$: binary non-zero support matrix
- Doubly-Permuted Homomorphic Encryption for Sparse Data:
- Choose encryption capacity $m \leq n \leq d$
- Encrypt $\mathbf{v}_i \in \mathbb{R}^n$: $\xi(\mathbf{v}_i)$
- Apply global permutation $\phi$ on $\mathbf{K}_i \in \{0,1\}^{d \times n}$: $\mathbf{K}'=\phi\mathbf{K}_i$
- Apply local permutation $\phi_i$ on $\mathbf{K}_i' \in \{0,1\}^{d \times n}$: $\mathbf{K}_i''=\phi_i\mathbf{K}_i'$
- Yonetani et. al., "Privacy-Preserving Visual Learning Using Doubly Permuted Homomorphic Encryption", ICCV 2017
Doubly-Permuted Homomorphic Encryption
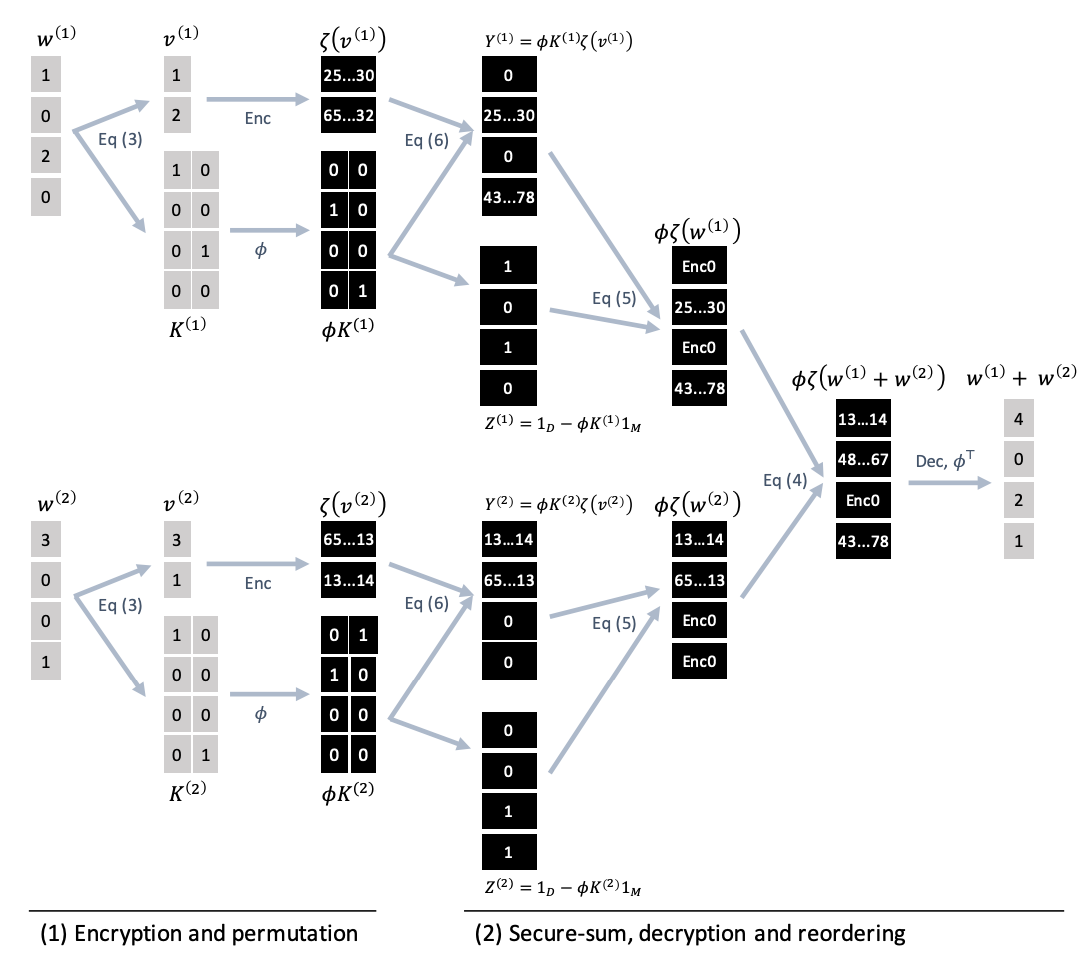
- Yonetani et. al., "Privacy-Preserving Visual Learning Using Doubly Permuted Homomorphic Encryption", ICCV 2017
Experiments: Real-World Evaluation


| Methods | Accuracy | Privacy |
|---|---|---|
| LLWT15 | 87 | No |
| DP | 78 | Yes |
| DP+SGD | 64 | Yes |
| Our Approach | 84 | Yes |


| Method | Average Precision | Privacy |
|---|---|---|
| DP | 0.546 | Yes |
| DP+SGD | 0.704 | Yes |
| Our Approach | 0.729 | Yes |
- Yonetani et. al., "Privacy-Preserving Visual Learning Using Doubly Permuted Homomorphic Encryption", ICCV 2017
Secure K-Nearest Neighbor Search
Privacy Leakage in Augmented Reality

- Pittaluga et. al., "Revealing Scenes by Inverting Structure from Motion Reconstructions", CVPR 2019
Information Leakage from Representations
- Learned Embeddings:
- Attacks on Embeddings:


- Mai et. al., "On the reconstruction of face images from deep face templates," IEEE Transactions on Pattern Analysis and Machine Intelligence, 2018
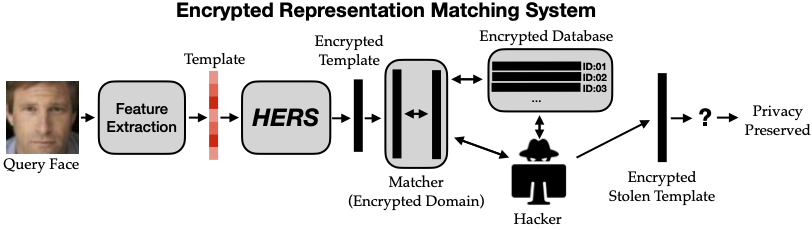
Secure Nearest Neigbhor Search
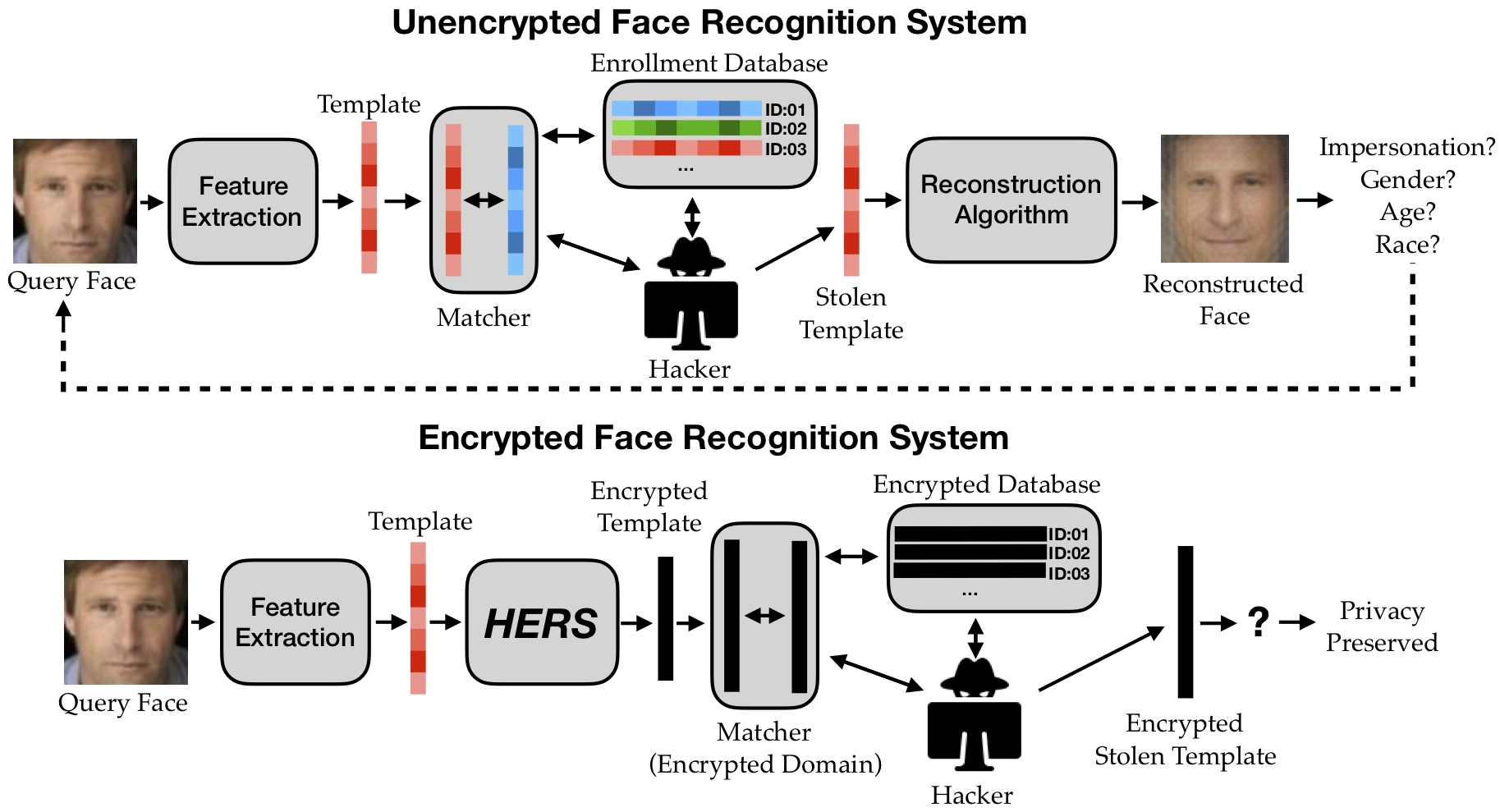
- Englesma, Jain, Boddeti, "HERS: Homomorphically Encrypted Representation Search,", Arxiv 2020
Enrollment Protocol
- Client Device:
- generates cryptographic keys
- captures image + extracts feature
- encrypts feature
- transmits encrypted feature + identity label to remote database




- V.N. Boddeti, "Secure Face Matching Using Fully Homomorphic Encryption,", BTAS 2018
Authentication Protocol
- Client Device:
- captures biometric signature + extracts feature, encrypts feature, transmits encrypted feature + claimed identity label to remote database
- Remote Database:
- homomorphic inner product between encrypted probe and gallery, transmits encrypted scores to client
- Client Device:
- decrypts received scores and makes decision






- V.N. Boddeti, "Secure Face Matching Using Fully Homomorphic Encryption,", BTAS 2018
Homomorphic Inner Products
- Feature Matching: \begin{eqnarray} \mbox{Euclidean Distance: } d(\mathbf{x},\mathbf{y}) &=& \|\mathbf{x}-\mathbf{y}\|^2_2 = \mathbf{x}^T\mathbf{x} + \mathbf{y}^T\mathbf{y} - 2\mathbf{x}^T\mathbf{y} \nonumber \\ \mbox{Cosine Similarity: } s(\mathbf{x},\mathbf{y}) &=& \frac{\mathbf{x}^T\mathbf{y}}{\|\mathbf{x}\|\|\mathbf{y}\|} \nonumber \end{eqnarray}
- Inner Product: \[\mathbf{x}^T\mathbf{y}=\sum_{i=1}^d x_iy_i\]
- Homomorphic Inner Product: \[s(\mathbf{x},\mathbf{y}) = \mathcal{D}\left(\sum_{i=1}^d \mathcal{E}(x_i, \mathbf{\theta}_e)\mathcal{E}(y_i, \mathbf{\theta}_e), \mathbf{\theta}_d\right)\]
Batching: Amortized Homomorphic Inner Product
- Inner Product: $d$ homomorphic multiplications + $d − 1$ homomorphic additions
- Complexity: homomorphic multiplication $>>>$ homomorphic addition
- Batching Inner Product: 1 homomorphic multiplications + $\log_2(d)$ homomorphic additions
- Template Size: batching size $<<<$ no batching size
- Key Idea: amortized inner product
- Encode entire vector at once + repetitive circular shift and addition

- V.N. Boddeti, "Secure Face Matching Using Fully Homomorphic Encryption,", BTAS 2018
Efficient Search with Dimensionality Reduction


- Englesma, Jain, Boddeti, "HERS: Homomorphically Encrypted Representation Search,", Arxiv 2020
Experimental Setup
- Datasets: ImageNet, MegaFace, Fingerprint-100M
- Models: ResNet, ArcFace, DeepPrint
- Options: feature quantization, security level, feature dimensionality

Computational Complexity
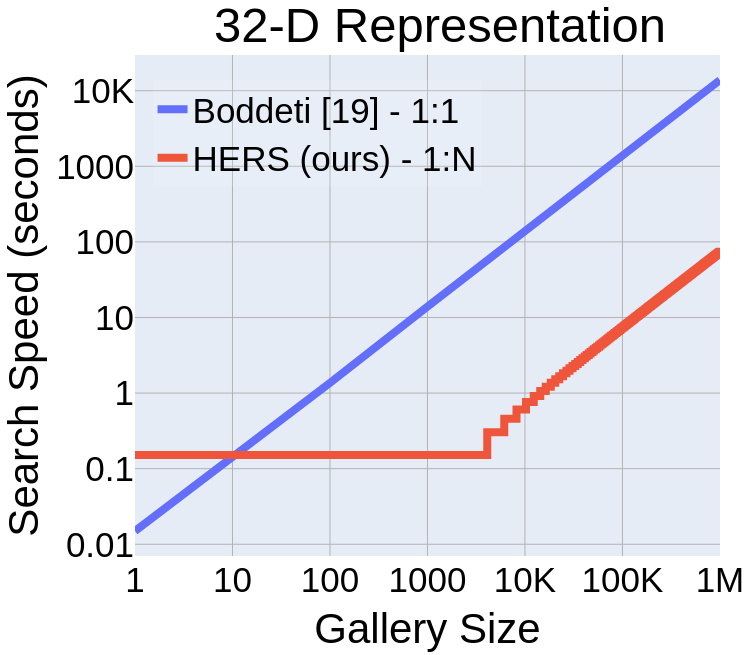
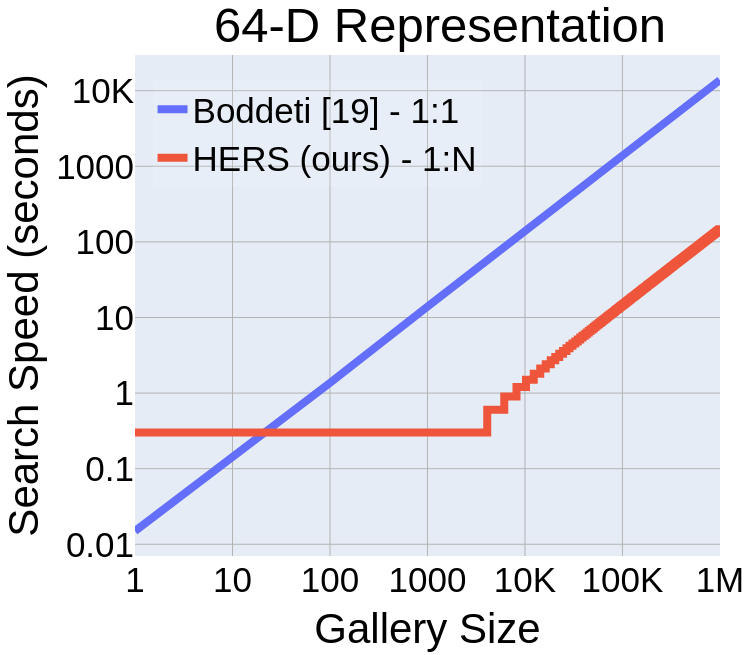
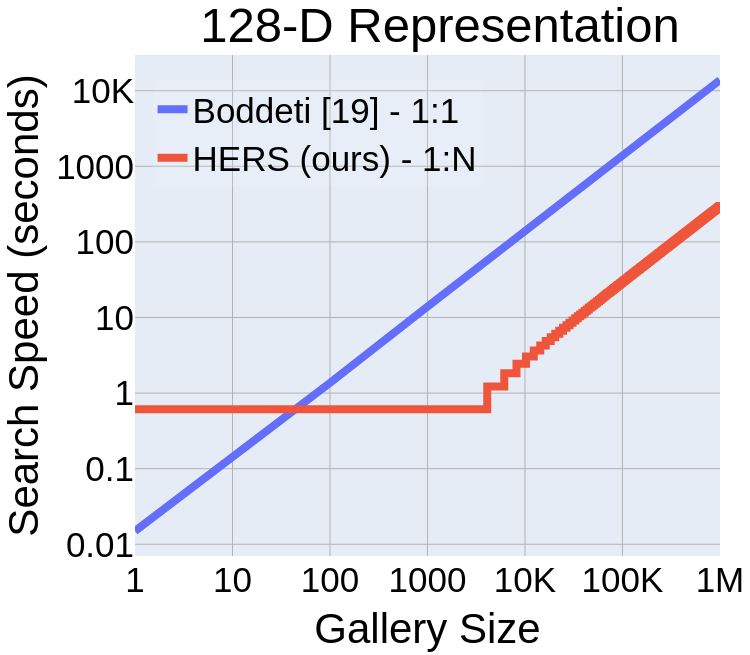
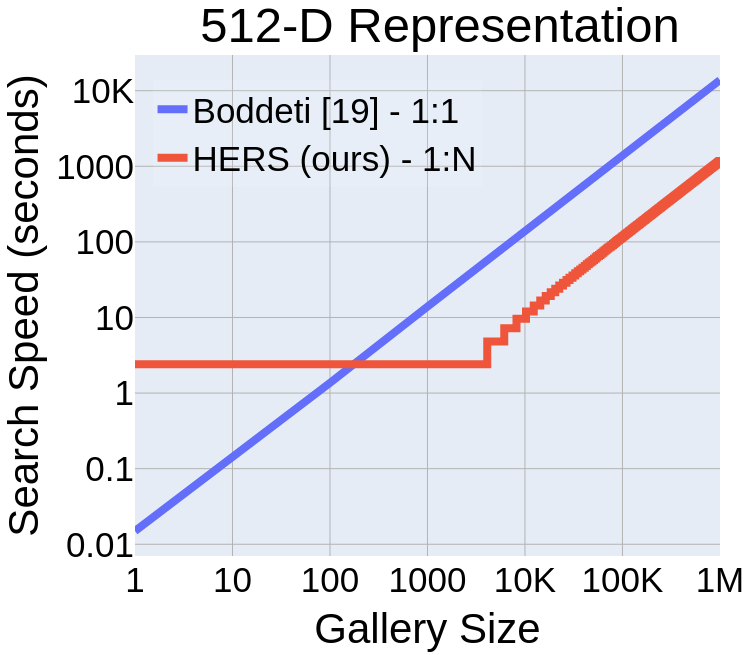

- Englesma, Jain, Boddeti, "HERS: Homomorphically Encrypted Representation Search,", Arxiv 2020
Image Retrieval

- Englesma, Jain, Boddeti, "HERS: Homomorphically Encrypted Representation Search,", Arxiv 2020
Encrypted Feature Matching (1-to-1)
Amortized Homomorphically Encrypted Inner Products



- V.N. Boddeti, "Secure Face Matching Using Fully Homomorphic Encryption,", BTAS 2018
Scalable Encrypted Search (1-to-$m$)
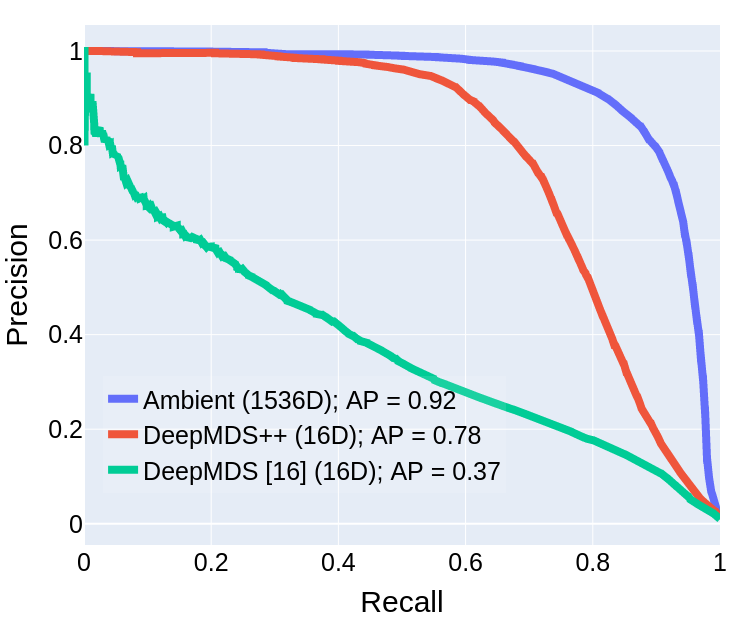
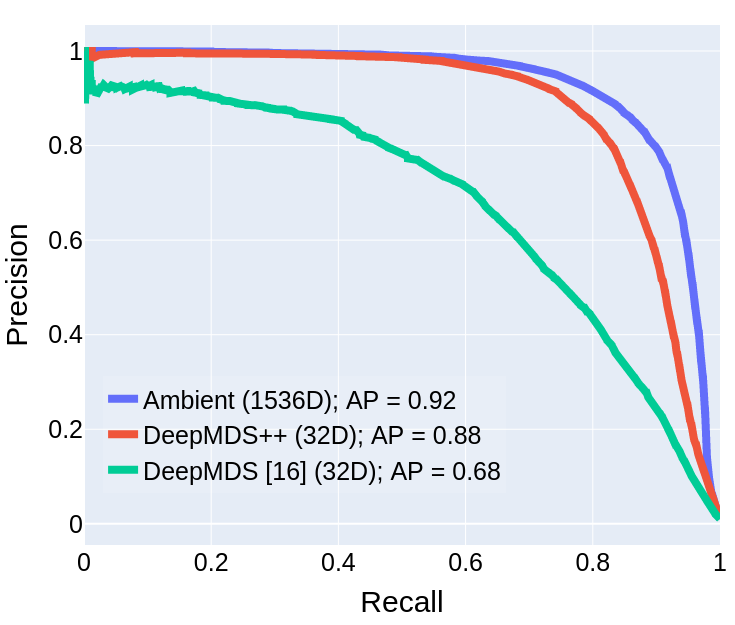


- Englesma, Jain, Boddeti, "HERS: Homomorphically Encrypted Representation Search,", Arxiv 2020
Two-Stage Search
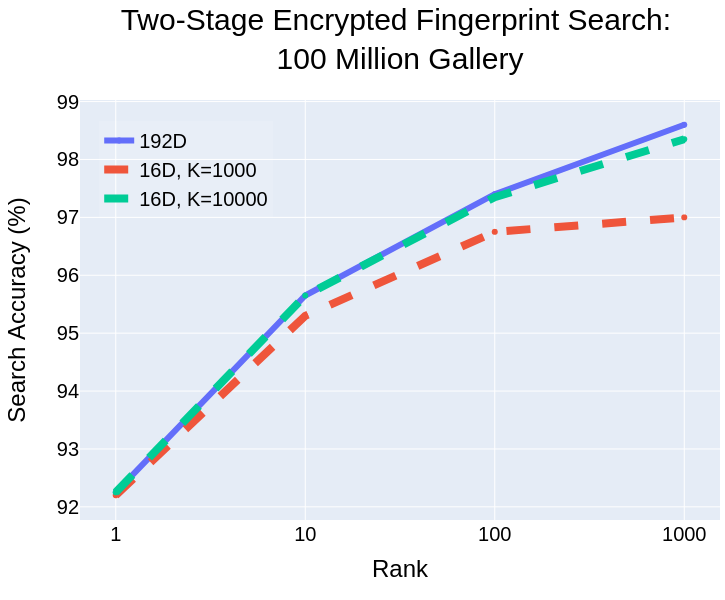
- Englesma, Jain, Boddeti, "HERS: Homomorphically Encrypted Representation Search,", Arxiv 2020
Summary
- Homomorphic encryption is a promising mechanism for privacy-preserving CV/ML.
- Doubly Permuted Homomorphic Encryption for Federated Learning: customized homomorphic encryption scheme for sparse data

- Practical Homomorphically Encrypted Image Search and Retrieval: customized data encoding schemes for 1-to-1 and 1-to-$m$ matching