Bayesian Networks: Representation
CSE 440: Introduction to Artificial Intelligence
Vishnu Boddeti
November 17, 2020
Content Credits: CMU AI, http://ai.berkeley.edu
Today
- Independence
- Bayes Net Introduction
Probabilistic Models
- Models describe how (a portion of) the world works
- Models are always simplifications
- May not account for every variable
- May not account for all interactions between variables
- "All models are wrong; but some are useful." – George E. P. Box
- What do we do with probabilistic models?
- We (or our agents) need to reason about unknown variables, given evidence
- Example: explanation (diagnostic reasoning)
- Example: prediction (causal reasoning)
- Example: value of information


Independence
Independence
- Two variables are independent if: \[\forall x,y: P(x,y) = P(x)P(y)\]
- This says that their joint distribution factors into a product two simpler distributions
- Another form: \[\forall x,y: P(x|y)=P(x)\]
- Usually written as: $X \perp \!\!\! \perp Y$
- Independence is a simplifying modeling assumption
- Empirical joint distributions: at best "close" to independent
- What could we assume for (Weather, Traffic, Cavity, Toothache)?
Example: Independence



Example: Independence
- N fair, independent coin flips:




Conditional Independence
- P(Toothache, Cavity, Catch)
- If I have a cavity, the probability that the probe catches it does not depend on whether I have a toothache:
- $P(+catch | +toothache, +cavity) = P(+catch | +cavity)$
- The same independence holds if I do not have a cavity:
- $P(+catch | +toothache, -cavity) = P(+catch| -cavity)$
- Catch is conditionally independent of Toothache given Cavity:
- $P(catch | toothache, cavity) = P(catch | cavity)$
- Equivalent statements:
- $P(toothache | catch , cavity) = P(toothache | cavity)$
- $P(toothache, catch | cavity) = P(toothache | cavity) P(catch | cavity)$
- One can be derived from the other easily
Conditional Independence
- Unconditional (absolute) independence very rare (why?)
- Conditional independence is our most basic and robust form of knowledge about uncertain environments.
- X is conditionally independent of Y given Z i.e., $X \perp \!\!\! \perp Y | Z$
- iff: \[\forall x,y,z: \mbox{ } P(x,y|z)=P(x|z)P(y|z)\]
- or, equivalently, iff \[\forall x,y,z: \mbox{ } P(x|y,z)=P(x|z)\]
Conditional Independence
- Example 1:
- T: Traffic
- U: Umbrella
- R: Raining
- Example 2:
- F: Fire
- S: Smoke
- A: Alarm
Conditional Independence and Chain Rule
- Chain rule: $P(X_1,X_2,\dots,X_n) = P(X_1)P(X_2|X_1)P(X_3|X_2,X_1) \dots $
- Trivial decomposition: \[P(T, R, U)=P(R)P(T|R)P(U|R,T)\]
- With assumption of conditional independence: \[P(T, R, U)=P(R)P(T|R)P(U|R)\]
- Bayes nets / graphical models help us express conditional independence assumptions
Bayes Net: Big Picture
Bayes Net: Big Picture
- Two problems with using full joint distribution tables as our probabilistic models:
- Unless there are only a few variables, the joint is WAY too big to represent explicitly
- Hard to learn (estimate) anything empirically about more than a few variables at a time
- Bayes nets: a technique for describing complex joint distributions (models) using simple, local distributions (conditional probabilities)
- More properly called probabilistic graphical models
- We describe how variables locally interact
- Local interactions chain together to give global, indirect interactions
Example Bayes Net: Insurance
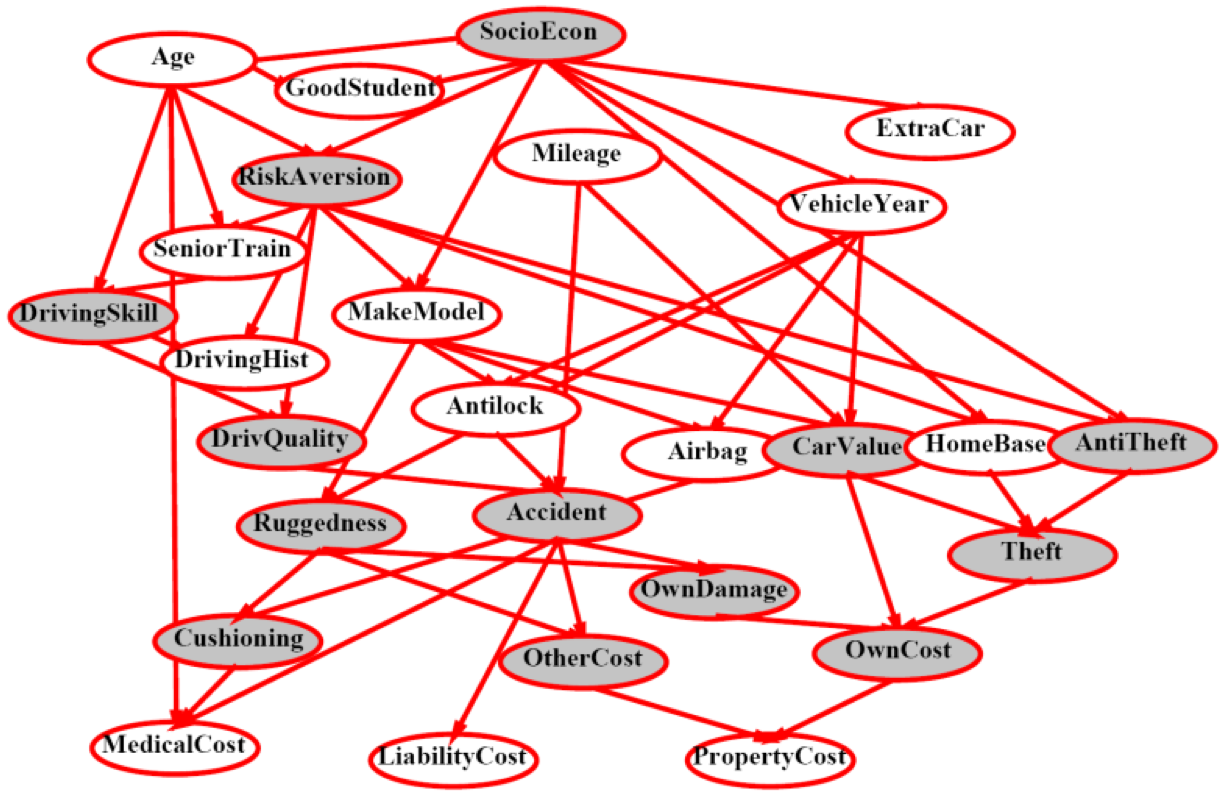
Example Bayes Net: Car

Graphical Model Notation
- Nodes: variables (with domains)
- Can be assigned (observed) or unassigned (unobserved)
- Arcs: interactions
- Similar to CSP constraints
- Indicate "direct influence" between variables
- Formally: encode conditional independence (more later)
- For now: imagine that arrows mean direct causation (in general, they don't.)

Example: Coin Flips
- N independent coin flips
- No interactions between variables: absolute independence

Example: Traffic
- Variables:
- R: it rains
- T: there is traffic
- Model 1: independence

- Model 2: rain causes traffic

- Why is an agent using model 2 better?
Example: Traffic II
- How do we build a causal graphical model?
- Variables:
- T: Traffic
- R: It rains
- L: Low pressure
- D: Roof drips
- B: Ballgame
- C: Cavity
Example: Alarm Network
- How do we build a causal graphical model?
- Variables:
- B: Burglary
- A: Alarm goes off
- M: Mary calls
- J: John calls
- E: Earthquake
Bayes Net Semantics
Bayes Net Semantics
- A set of nodes, one per variable $X$
- A directed, acyclic graph
- A conditional distribution for each node
- A collection of distributions over $X$, one for each combination of parents' values \[P(X|a_1,\dots,a_n)\]
- CPT: conditional probability table
- Description of a noisy "causal" process

A Bayes net = Topology (graph) + Local Conditional Probabilities
Probabilities in BNs
- Bayes nets implicitly encode joint distributions
- As a product of local conditional distributions
- To see what probability a BN gives to a full assignment, multiply all the relevant conditionals together: \[P(x_1,\dots,x_n) = \prod_{i=1}^n P(x_i|parents(x_i))\]
- Example: $P(+cavity,+catch,-toothache)$
Probabilities in BNs
- Why are we guaranteed that setting the following results in a proper joint distribution? \[P(x_1,\dots,x_n) = \prod_{i=1}^n P(x_i|parents(x_i)) \]
- Chain rule (valid for all distributions): \[P(x_1,\dots,x_n) = \prod_{i=1}^n P(x_i|x_1,\dots,x_{i-1})\]
- Assume conditional independences: \[P(x_i|x_1,\dots,x_{i-1}) = P(x_i|parents(x_i)) \]
- Consequence: $P(x_1,\dots,x_n)=\prod_{i=1}^n P(x_i|parents(x_i))$
- Not every BN can represent every joint distribution
- The topology enforces certain conditional independencies
Example: Coin Flips



Example: Traffic


Example: Traffic
- Causal direction

Example: Reverse Traffic
- Reverse Causality?

Causality
- When Bayes nets reflect the true causal patterns:
- Often simpler (nodes have fewer parents)
- Often easier to think about
- Often easier to elicit from experts
- BNs need not actually be causal
- Sometimes no causal net exists over the domain (especially if variables are missing)
- E.g. consider the variables Traffic and Drips
- End up with arrows that reflect correlation, not causation
- What do the arrows really mean?
- Topology may happen to encode causal structure
- Topology really encodes conditional independence \[P(x_i|x_1,\dots,x_{i-1})=P(x_i|parents(x_i))\]
Bayes Net
- So far: how a Bayes net encodes a joint distribution
- Next: how to answer queries about that distribution
- Today:
- First assembled BNs using an intuitive notion of conditional independence as causality
- Then saw that key property is conditional independence
- Main goal: answer queries about conditional independence and influence
- After that: how to answer numerical queries (inference)
