Particle Filters


CSE 440: Introduction to Artificial Intelligence

Vishnu Boddeti

December 08, 2020


Content Credits: CMU AI, http://ai.berkeley.edu

Today

  • Particle Filters

  • Most Likely Explanation Queries (Vitterbi Algorithm)

  • Applications:
    • Robot Localization and Mapping
    • Speech Recognition

Recap: Reasoning over Time

  • Markov models
  • Hidden Markov models


$X$ $E$ $P$
rain umbrella 0.9
rain no umbrella 0.1
sun umbrella 0.2
sun no umbrella 0.8

Filtering

  • Elapse time: compute $P(X_{t+1}|e_{1:t})$ \[P(x_{t+1}|e_{1:t}) = \sum_{x_{t}}P(x_{t}|e_{1:t})\cdot P(x_{t+1}|x_{t})\]
  • Observe: compute $P(X_{t+1}|e_{1:t+1})$ \[P(X_{t+1}|e_{1:t+1}) \propto P(x_{t+1}|e_{1:t})\cdot P(e_{t+1}|x_{t+1})\]

Belief: $\left(P(rain), P(sun)\right)$
$P(X_1)$ $(0.5, 0.5)$ Prior on $X_1$
$P(X_1|E_1=+U)$ (0.82, 0.18) Observe
$P(X_2|E_1=+U)$ (0.63, 0.37) Elapse Time
$P(X_2|E_1=+U, E_2=+U)$ (0.88, 0.12) Observe

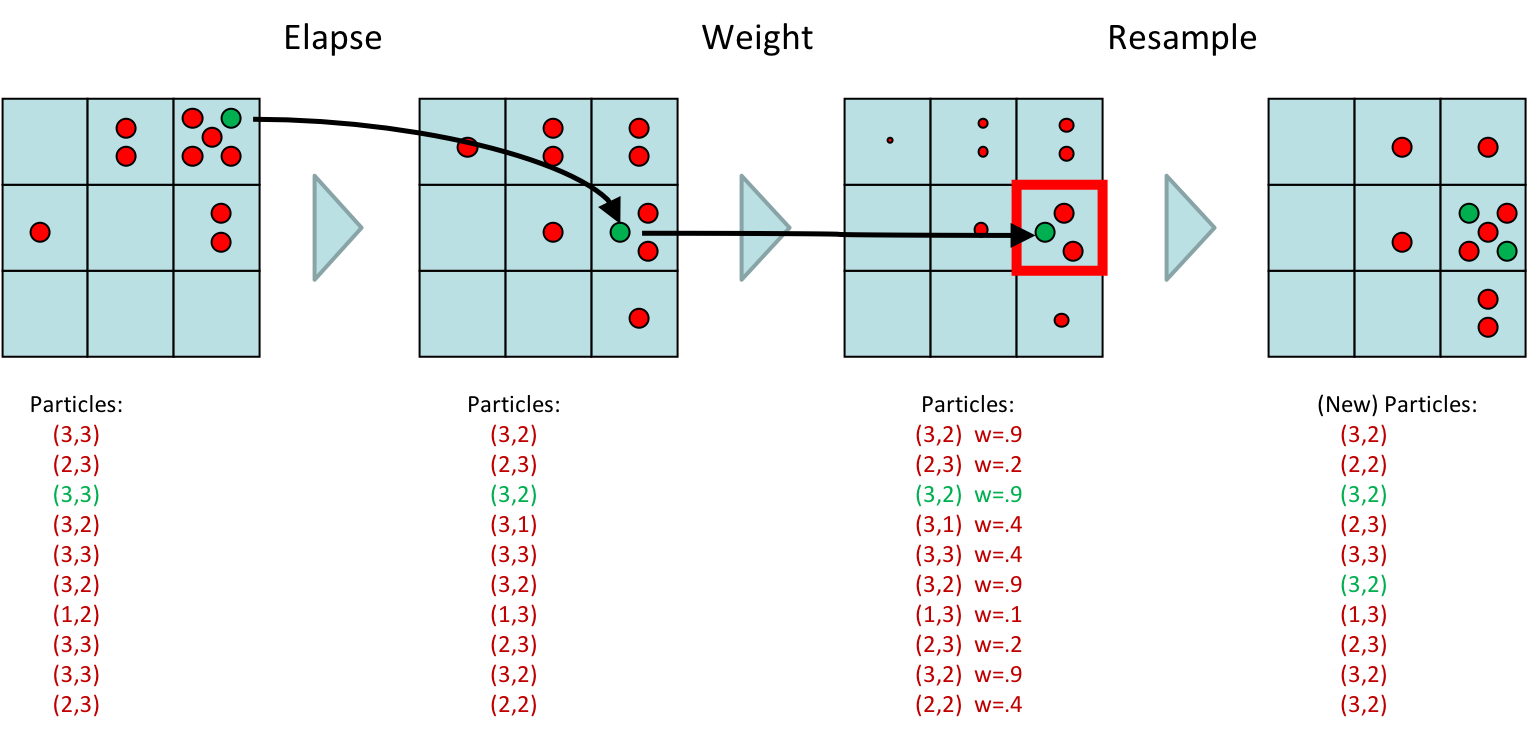
Particle Filtering

Particle Filtering

  • Filtering: approximate solution
  • Sometimes $|X|$ is too big to use exact inference
    • $|X|$ may be too big to even store $B(X)$
    • E.g. when $X$ is continuous
  • Solution: approximate inference
    • Track samples of $X$, not all values
    • Samples are called particles
    • Time per step is linear in the number of samples
    • But: number needed may be large
    • In memory: list of particles, not states
  • This is how robot localization works in practice
  • Particle is just new name for sample
$P(X)$
0.0 0.1 0.0
0.0 0.1 0.2
0.0 0.2 0.5

Representation: Particles

  • Our representation of $P(X)$ is now a list of $N$ particles (samples)
    • Generally, $N << |X|$
    • Storing map from $X$ to counts would defeat the point
  • $P(x)$ approximated by number of particles with value $x$
    • So, many $x$ may have $P(x) = 0$
    • More particles, more accuracy
  • For now, all particles have a weight of 1

Particle Filtering: Elapse Time

  • Each particle is moved by sampling its next position from the transition model
    • \[x' = sample(P(X'|x))\]
    • This is like prior sampling – samples’ frequencies reflect the transition probabilities
    • Here, most samples move clockwise, but some move in another direction or stay in place
  • This captures the passage of time
    • If enough samples, close to exact values before and after (consistent)

Particle Filtering: Observe

  • Slightly trickier:
    • Do not sample observation, fix it
    • Similar to likelihood weighting, downweight samples based on the evidence \begin{equation} \begin{aligned} w(x) &= P(e|x) \nonumber \\ B(X) &\propto P(e|X)B'(X) \nonumber \end{aligned} \end{equation}
    • As before, the probabilities don’t sum to one, since all have been downweighted (in fact they now sum to ($N$ times) an approximation of $P(e)$)

Particle Filtering: Resample

  • Rather than tracking weighted samples, we resample
  • $N$ times, we choose from our weighted sample distribution (i.e. draw with replacement)
  • This is equivalent to renormalizing the distribution
  • Now the update is complete for this time step, continue with the next one

Summary: Particle Filtering

  • Particles: track samples of states rather than an explicit distribution

Robot Localization

  • In robot localization:
    • We know the map, but not the robot’s position
    • Observations may be vectors of range finder readings
    • State space and readings are typically continuous (works basically like a very fine grid) and so we cannot store $B(X)$
    • Particle filtering is a main technique

Particle Filter Localization (Sonar)

Robot Mapping

  • SLAM: Simultaneous Localization And Mapping
    • We do not know the map or our location
    • State consists of position AND map
    • Main techniques: Kalman filtering (Gaussian HMMs) and particle methods

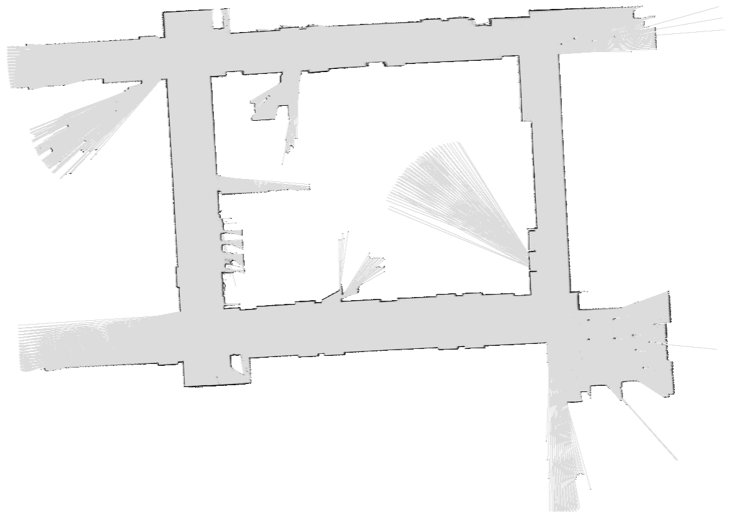
Particle Filter SLAM - Video 1

Particle Filter SLAM - Video 2

Dynamic Bayes Net

Dynamic Bayes Nets (DBNs)

  • We want to track multiple variables over time, using multiple sources of evidence
  • Idea: Repeat a fixed Bayes net structure at each time
  • Variables from time t can condition on those from $t-1$
  • Dynamic Bayes nets are a generalization of HMMs

Exact Inference in DBNs

  • Variable elimination applies to dynamic Bayes nets
  • Procedure: "unroll" the network for T time steps, then eliminate variables until $P(X_T|e_{1:T})$ is computed
  • Online belief updates: Eliminate all variables from the previous time step; store factors for current time only

DBN Particle Filters

  • A particle is a complete sample for a time step
  • Initialize: Generate prior samples for the t=1 Bayes net
    • Example particle: $G_2^a = (3,3)$ $G_1^b=(5,3)$
  • Elapse time: Sample a successor for each particle
    • Example successor: $G_2^a = (2,3)$ $G_2^b=(6,3)$
  • Observe: Weight each entire sample by the likelihood of the evidence conditioned on the sample
    • Likelihood: $P(E_1^a|G_1^a) \times P(E_1^b|G_1^b)$
  • Resample: Select prior samples (tuples of values) in proportion to their likelihood

Most Likely Explanation

HMMs: MLE Queries

  • HMMs defined by:
    • States $X$
    • Observations $E$
    • Initial distribution: $P(X_1)$
    • Transitions: $P(X_t|X_{t-1})$
    • Emissions: $P(E_t|X_t)$
  • New query: most likely explanation: $\underset{x_{1:t}}{\operatorname{arg max}} P(x_{1:t}|e_{1:t})$
  • New method: the Viterbi algorithm

State Trellis

  • State trellis: graph of states and transitions over time
  • Each arc represents some transition $x_{t-1} \rightarrow x_t$
  • Each arc has weight $P(x_t|x_{t-1})P(e_t|x_t)$
  • Each path is a sequence of states
  • The product of weights on a path is that sequence's probability along with the evidence
  • Forward algorithm computes sums of paths, Viterbi computes best paths

Forward/Viterbi Algorithms

Forward Algorithm (Sum)
\begin{equation} \begin{aligned} f_t[x_t] &= P(x_t, e_{1:t}) \nonumber \\ &= P(e_t|x_t)\sum_{x_{t-1}} P(x_t|x_{t-1})f_{t-1}[x_{t-1}] \nonumber \end{aligned} \end{equation}
Viterbi Algorithm (Max)
\begin{equation} \begin{aligned} m_t[x_t] &= \max_{x_{1:t-1}} P(x_{1:t-1}, x_t, e_{1:t}) \nonumber \\ &= P(e_t|x_t)\max_{x_{t-1}} P(x_t|x_{t-1})m_{t-1}[x_{t-1}] \nonumber \end{aligned} \end{equation}

Speech Recognition

Speech Recognition in Action

Basics of Speech

  • Speech input is an acoustic waveform.

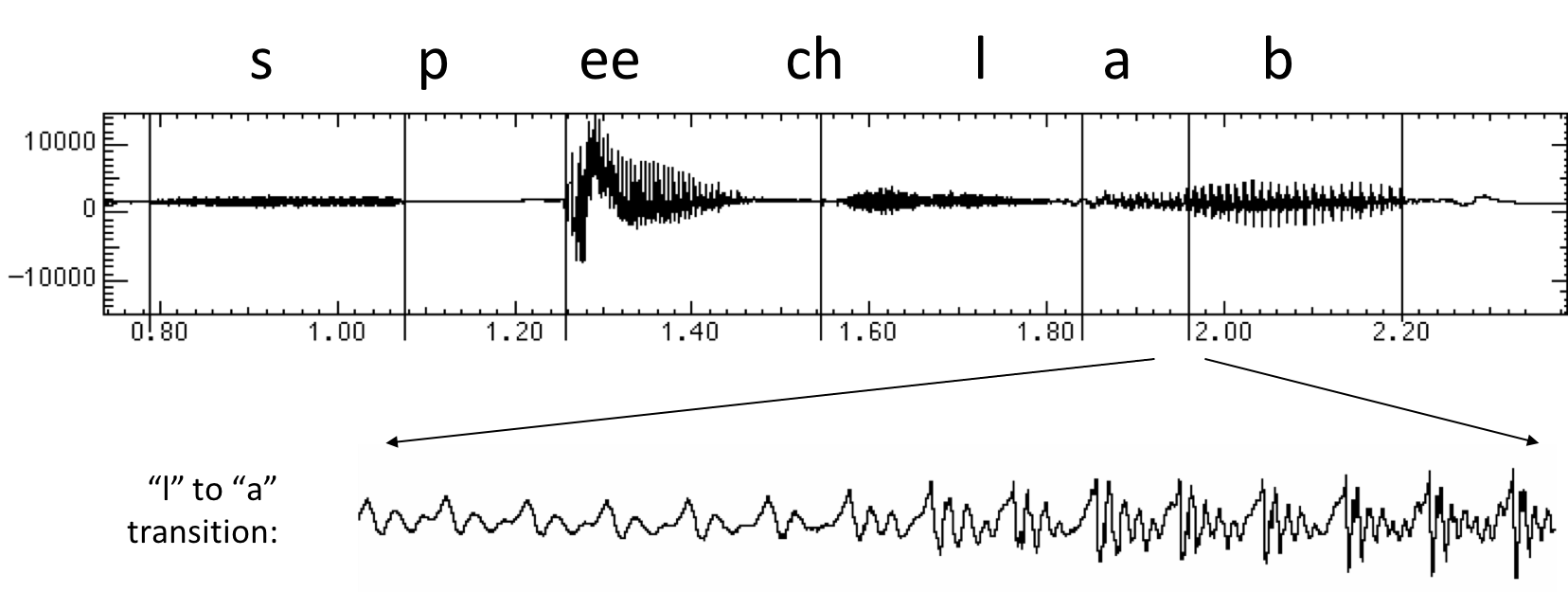
Spectral Analysis

  • Frequency gives pitch; amplitude gives volume
    • Sampling at ~8 kHz (phone), ~16 kHz (mic) (kHz=1000 cycles/sec)
  • Fourier transform of wave displayed as a spectrogram
    • Darkness indicates energy at each frequency

Acoustic Feature Sequence

  • Time slices are translated into acoustic feature vectors ($\sim$39 real numbers per slice)
  • These are the observations $E$, now we need the hidden states $X$

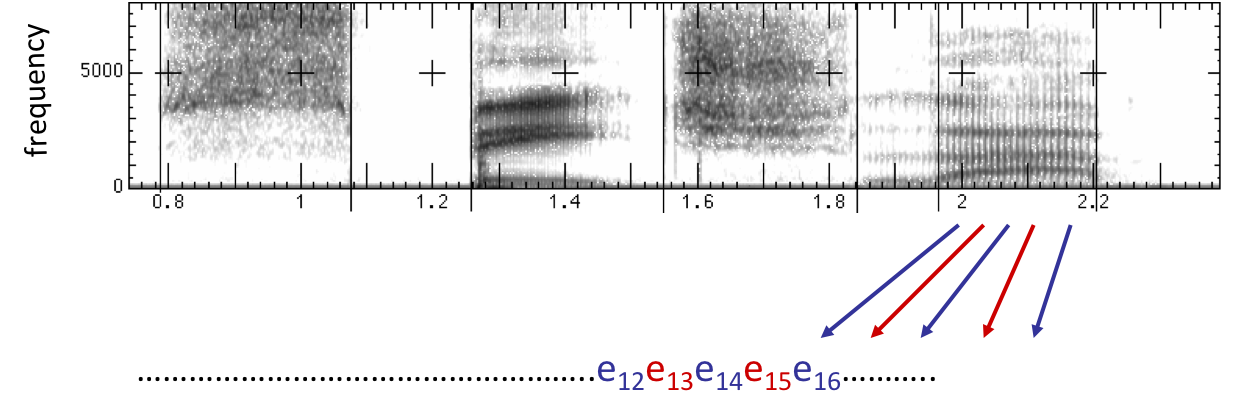
Speech State Space

  • HMM Specification
    • $P(E|X)$ encodes which acoustic vectors are appropriate for each phoneme (each kind of sound)
    • $P(X|X')$ encodes how sounds can be strung together
  • State Space
    • We will have one state for each sound in each word
    • Mostly, states advance sound by sound
    • Build a little state graph for each word and chain them together to form the state space $X$

States in a Word

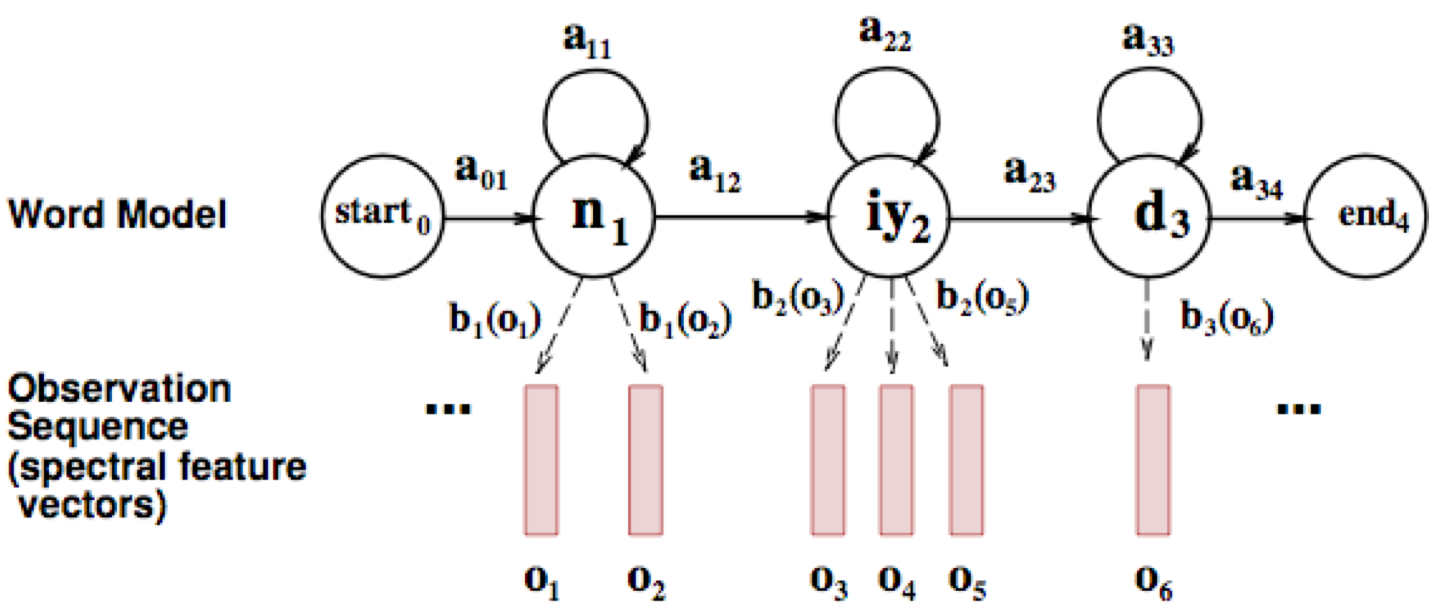
Transitions with a Bigram Model

\begin{equation} \begin{aligned} \hat{P}(door|the) &= \frac{14112454}{23135851162} \nonumber \\ &= 0.0006 \nonumber \end{aligned} \end{equation}

Decoding

  • Finding the words given the acoustics is an HMM inference problem
  • Which state sequence $x_{1:T}$ is most likely given the evidence $e_{1:T}$? \[x^*_{1:T} = \underset{x_{1:T}}{\operatorname{arg max}}P(x_{1:T}|e_{1:T}) = \underset{x_{1:T}}{\operatorname{arg max}} P(x_{1:T},e_{1:T})\]
  • From the sequence $x$, we can simply read off the words

Results