Optimization
CSE 891: Deep Learning
Vishnu Boddeti
Wednesday September 23, 2020
Gradient Descent
- Gradient Descent: procedure to minimize a function
- Optimizes a linear approximation of the function at the given point. \[f(\mathbf{x}) = f(\mathbf{x}_0) + (\mathbf{x}-\mathbf{x}_0)^T\nabla_{\mathbf{x}}f(\mathbf{x}_0)\]
- compute gradient \[f'(\mathbf{x}_0) = \nabla_{\mathbf{x}}f(\mathbf{x}_0)\]
- take step in opposite direction \[\Delta \mathbf{x}_0 = -\nabla_{\mathbf{x}}f(\mathbf{x}_0)\]
Gradient Descent
- Gradient descent for empirical risk minimization
- initialize $\mathbf{\theta}$
- for T iterations $$ \begin{eqnarray} \nabla_{\mathbf{\theta}}J(\mathbf{\theta}) &=& \frac{1}{N}\sum_n\nabla_{\theta}l(f(\mathbf{x}_n;\mathbf{\theta}),\mathbf{y}_n)+\lambda\nabla_{\mathbf{\theta}}\Omega(\mathbf{\theta}) \nonumber \\ \mathbf{\theta}_{t+1} &=& \mathbf{\theta}_{t} - \alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta}_t) \nonumber \end{eqnarray} $$
Second Order Gradient Descent
- Second Order Taylor Approximation: $$ \begin{eqnarray} f(\mathbf{x}) &=& f(\mathbf{x}_0) + (\mathbf{x}-\mathbf{x}_0)^T\nabla_{\mathbf{x}}f(\mathbf{x}_0) + \frac{1}{2}(\mathbf{x}-\mathbf{x}_0)^T\nabla^2_{\mathbf{x}}f(\mathbf{x}_0)(\mathbf{x}-\mathbf{x}_0) \nonumber \end{eqnarray} $$
- Newton Update: $$ \begin{eqnarray} \nabla_{\mathbf{x}}f(\mathbf{x}) &=& 0 \nonumber \\ \nabla_{\mathbf{x}}f(\mathbf{x}_0) + \nabla^2_{\mathbf{x}}f(\mathbf{x}_0)(\mathbf{x}-\mathbf{x}_0) &=& 0 \nonumber \\ \mathbf{x} &=& \mathbf{x}_0 - \left[\nabla^2_{\mathbf{x}}f(\mathbf{x}_0)\right]^{-1}\nabla_{\mathbf{x}}f(\mathbf{x}_0) \nonumber \end{eqnarray} $$
- Practically infeasible for large problems
- Many approximations (quasi-newton methods) have been proposed in the literature (BFGS, L-BFGS etc.)
Variants of Gradient Descent
- Batch Gradient Descent: \[\Delta_{\mathbf{\theta}} = \frac{1}{N}\sum_n\nabla_{\theta}l(f(\mathbf{x}_n;\mathbf{\theta}),\mathbf{y}_n)\]
- Stochastic Gradient Descent: \[\Delta_{\mathbf{\theta}} = \nabla_{\theta}l(f(\mathbf{x}_n;\mathbf{\theta}),\mathbf{y}_n)\]
- Mini-Batch Gradient Descent: \[\Delta_{\mathbf{\theta}} = \frac{1}{m}\sum_{n \in M}\nabla_{\theta}l(f(\mathbf{x}_n;\mathbf{\theta}),\mathbf{y}_n)\]
Stochastic Gradient Descent
- Algorithm that performs updates after each example.
- initialize $\mathbf{\theta}$
- for N iterations:
- for each training example $(\mathbf{x}_n,\mathbf{y}_n)$ $$\begin{eqnarray} J(\mathbf{\theta}) &=& \frac{1}{m}\sum_{n \in M} l(f(\mathbf{x}_n,\mathbf{\theta}),\mathbf{y}_n) + \lambda\Omega(\mathbf{\theta}) \nonumber \\ \mathbf{\theta}_t &=& \mathbf{\theta}_{t-1} - \alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta}_{t-1}) \nonumber \end{eqnarray}$$
- $\alpha$ is the learning rate.
- very important hyperparameter
- typically follows an annealing schedule
SGD With Noise
- Another variant: use noisy gradients
- Anneal the noise down with iterations
Saddle Points

- A saddle point is a point where:
- $\nabla \mathcal{L}(\mathbf{\theta})=\mathbf{0}$
- The Hessian $\mathbf{H}(\mathbf{\theta})$ has some positive and some negative eigenvalues, i.e., some directions with positive curvature and some with negative curvature
Saddle Points: A Problem?
- When would saddle points be a problem?
- Suppose you have two hidden units with identical incoming and outgoing weights.
- After a gradient descent update, they will still have identical weights. By induction, they’ll always remain identical.
- But if you perturbed them slightly, they can start to move apart.
- Important special case: never initialize all your weights to zero!
- Instead, break the symmetry by using small random values.
Plateaux
- An important example of a plateau is a saturated unit. This is when it is in the flat region of its activation function. Recall the backprop equation for the weight derivative:
$$\begin{equation}
\begin{aligned}
z_i' &= h'\phi'(z) \\
w_{ij}' &= z_i'x_j
\end{aligned}
\end{equation}$$

- If $\phi'(z_i)$ is always close to zero, then the weights will get stuck.
- If there is a ReLU unit whose input $z_i$ is always negative, the weight derivatives will be exactly $0$. We call this a dead unit.
Momentum
- Unfortunately, even with these normalization tricks, ill-conditioned curvature is a fact of life. We need algorithms that are able to deal with it.
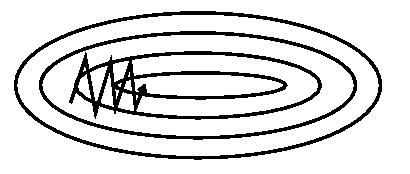
- Momentum:
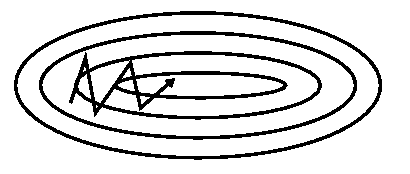
- Nesterov Accelerated Gradient:
$$\begin{eqnarray}
\mathbf{v}_t &=& \gamma\mathbf{v}_{t-1} + \alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta}) \nonumber \\
\mathbf{\theta}_t &=& \mathbf{\theta}_{t-1} - \mathbf{v}_t \nonumber
\end{eqnarray}$$
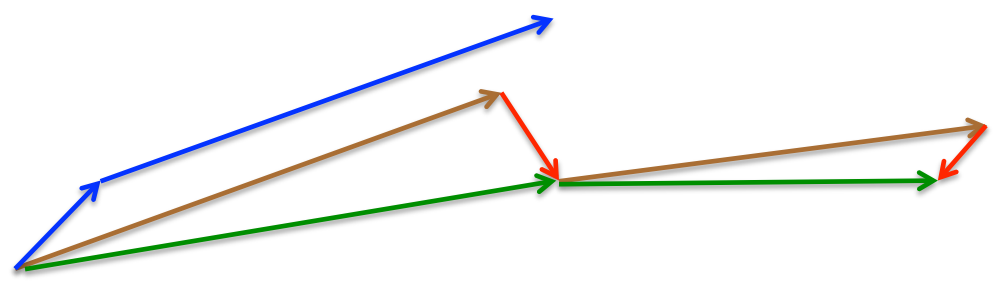
$$\begin{eqnarray}
\mathbf{v}_t &=& \gamma\mathbf{v}_{t-1} + \alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta-\gamma\mathbf{v}_{t-1}}) \nonumber \\
\mathbf{\theta}_t &=& \mathbf{\theta}_{t-1} - \mathbf{v}_t \nonumber
\end{eqnarray}$$
Why Momentum
- In the high curvature directions, the gradients cancel each other out, so momentum dampens the oscillations.
- In the low curvature directions, the gradients point in the same direction, allowing the parameters to pick up speed.
- If the gradient is constant (i.e. the cost surface is a plane), the parameters will reach a terminal velocity of $$ -\frac{\alpha}{1-\gamma}\cdot \frac{\partial \mathcal{L}}{\partial \mathbf{\theta}} $$
- This suggests if you increase $\gamma$, you should lower $\alpha$ to compensate.
- Momentum sometimes helps a lot, and almost never hurts.
Adam
- Adapt learning rate by using moments of gradients
- First and Second Order Moments: $$ \begin{eqnarray} \mathbf{m}_t &=& \beta_1 \mathbf{m}_{t-1} + (1-\beta_1)\mathbf{g}_t \\ \mathbf{v}_t &=& \beta_1 \mathbf{v}_{t-1} + (1-\beta_1)\mathbf{g}^2_t \end{eqnarray} $$
- Bias Correction: $$ \begin{eqnarray} \mathbf{\hat{m}}_t = \frac{\mathbf{m}_t}{1-\beta_1} \nonumber \\ \mathbf{\hat{v}}_t = \frac{\mathbf{v}_t}{1-\beta_1} \nonumber \end{eqnarray} $$
- Adam Update: $$ \begin{equation} \mathbf{\theta}_t = \mathbf{\theta}_{t-1} - \frac{\alpha}{\sqrt{\mathbf{\hat{v}}_t+\epsilon}}\mathbf{\hat{m}}_t \end{equation} $$
$L_2$ Regularization vs Weight Decay
- $L_2$ regularization and weight decay are equivalent for SGD and SGD+Momentum.
- But they are not the same for adaptive methods (AdaGrad, RMSprop, Adam etc.)
- AdamW decouples weight decay.
- It should be your default optimizer
In Practice...
- Adam/AdamW is a good default choice.
- In many cases SGD+Momentum can outperform Adam but may require more tuning.
- If you can afford to do full batch updates, then try out L-BFGS.