Graph Neural Networks - I
CSE 891: Deep Learning
Vishnu Boddeti
Monday October 26, 2020
Traditional Neural Networks
- Deep neural networks that exploit:
- translational equivariance (weight sharing)
- heirarchical compositionality
- Data Domain:
- Images, volumes, videos lie on 2D, 3D, 2D+1 Euclidean domains (grids)
- Sentences, words, speech lie on 1D Euclidean domain
- These domains have strong regular spatial structures.
- All ConvNet operatiions are mathemtically well defined and fast (convolution, pooling)





Convolutional Neural Networks on Grids

- CNNs nicely exploit the grid structure of data.

- 2D convolutional operator as applied to a grid-structured input (e.g., image)
- Slide Credit: Xavier Bresson
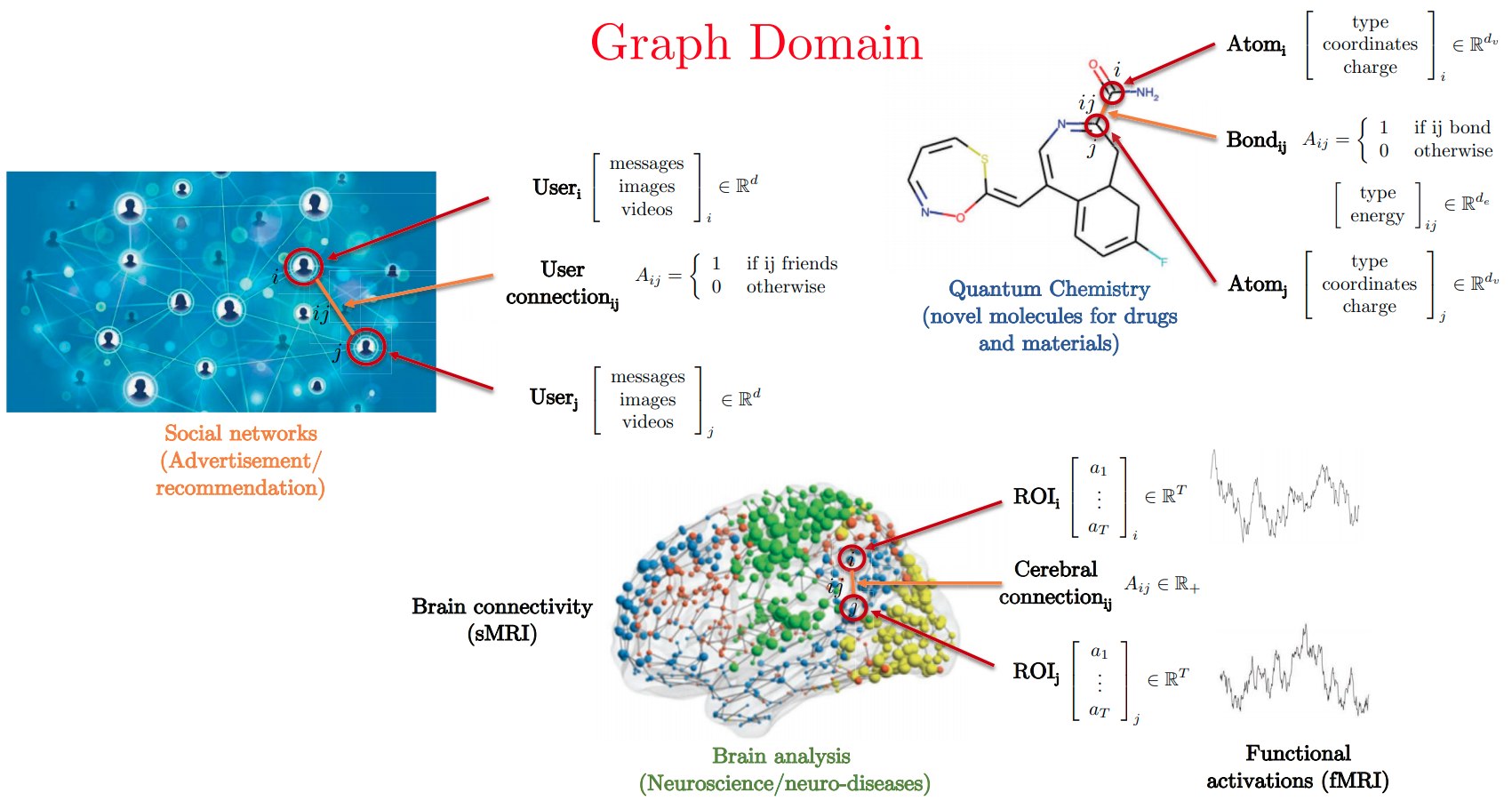
Graph Structured Data

Standard CNN and RNN architectures don't work on this data.
- Slide Credit: Xavier Bresson
Graph Definition
- Graphs $\mathcal{G}$ are defined by:
- Vertices $V$
- Edges $E$
- Adjacency matrix $\mathbf{A}$
- Features:
- Node features: $\mathbf{h}_i, \mathbf{h}_j$ (user type)
- Edge features: $\mathbf{e}_{ij}$ (relation type)
- Graph features: $\mathbf{g}$ (network type)

Convolution

- How to define convolution?
- Definition #1: convolution as template matching in spatial domain
- Update Rule: $$\begin{equation} h^{(l+1)}_4 = \sigma\left(w^l_0h_0^l+w^l_1h_1^l+\dots+w^l_8h_8^l\right) \end{equation}$$
- All nodes of the template $w_i$ are always ordered/positioned the same way!
Graph Convolution
- Can we extend template matching to graphs?
- Main issue #1:
- No node ordering: How to match template features with data features when nodes have no given position (index is not a position)?
- The correspondence of nodes is lost on graphs. There is no up, down, right and left on graphs.
- Matching scores have no meaning as they do not compare the same information.
Graph Convolution
- Can we extend template matching to graphs?
- Main issue #2:
- Heterogeneous neighborhood : How to deal with different neighborhood sizes?


Graph Convolution

Convolution
- How to define convolution?
- Definition #2: convolution theorem in spectral domain
- Fourier transform of the convolution of two functions is the pointwise product of their Fourier transforms $$\begin{equation} \mathcal{F}(\mathbf{w} \ast \mathbf{h}) = \mathcal{F}(\mathbf{w}) \odot \mathcal{F}(\mathbf{h}) \Longrightarrow \mathbf{w} \ast \mathbf{h} = \mathcal{F}^{-1}(\mathcal{F}(\mathbf{w}) \odot \mathcal{F}(\mathbf{h})) \end{equation}$$
- Generic Fourier transform has $\mathcal{O}(n^2)$ complexity, but if the domain is a grid then complexity can be reduced to $\mathcal{O}(n\log n)$ with FFT.
Graph Convolution
- Can we extend convolution theorem to graphs?
- How to define Fourier transform for graphs?
- How to compute fast spectral convolutionsin $\mathcal{O}(n)$ time for compact kernels? $$\begin{equation} \mathbf{w} \ast_{\mathcal{G}} \mathbf{h} = \mathcal{F}^{-1}_{\mathcal{G}}(\mathcal{F}_{\mathcal{G}}(\mathbf{w}) \odot \mathcal{F}_{\mathcal{G}}(\mathbf{h})) \end{equation}$$
Spatial vs Spectral
- Two major approaches to build Graph CNNs
- Spatial Domain
- Perform convolution in spatial domain similar to images (euclidean data) with shareable weight parameters
- Spectral Domain
- Convert Graph data to spectral domain data by using the eigenvectors of laplacian operator on the graph data and perform learning on the transformed data.
Spectral Graph ConvNets
Spectral Convolution
- Spectral Graph Theory
- Book by Fan Chung. Includes harmonic analysis, graph theory, combinatorial problems, optimization etc.
- How to perform spectral convolution?
- Graph Laplacian
- Fourier functions
- Fourier transform
- Convolution Theorem
Graph Laplacian
- Core operator in Spectral Graph Theory
- Represented as a positive semi-definite $n\times n$ matrix
- Unnormalized Laplacian: $\Delta = \mathbf{D}-\mathbf{A}$
- Normalized Laplacian: $\begin{equation}\Delta = \mathbf{I} - \mathbf{D}^{-1/2}\mathbf{A}\mathbf{D}^{-1/2}\end{equation}$
- Randomwalk Laplacian: $\begin{equation}\Delta = \mathbf{I} - \mathbf{D}^{-1}\mathbf{A}\end{equation}$
- where $\mathbf{D}=diag(\sum_{i \neq j}A_{ij})$
- Interpretation:
- Measure of smoothness : Difference between local value $\mathbf{h}_i$ and its neighborhood average values $\mathbf{h}_j$.
Fourier Functions

- Slide Credit: Xavier Bresson
Fourier Functions
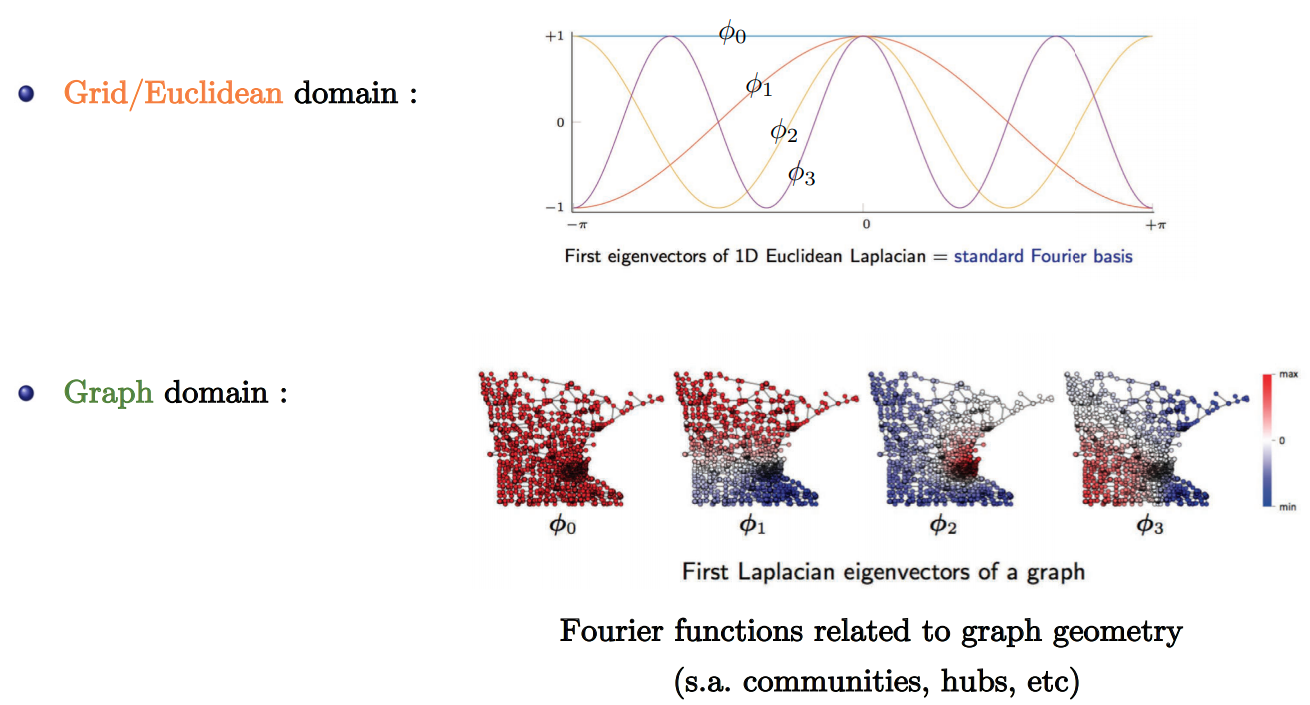
- Slide Credit: Xavier Bresson
Fourier Functions

Fourier Transform

- Slide Credit: Xavier Bresson
Convolution Theorem
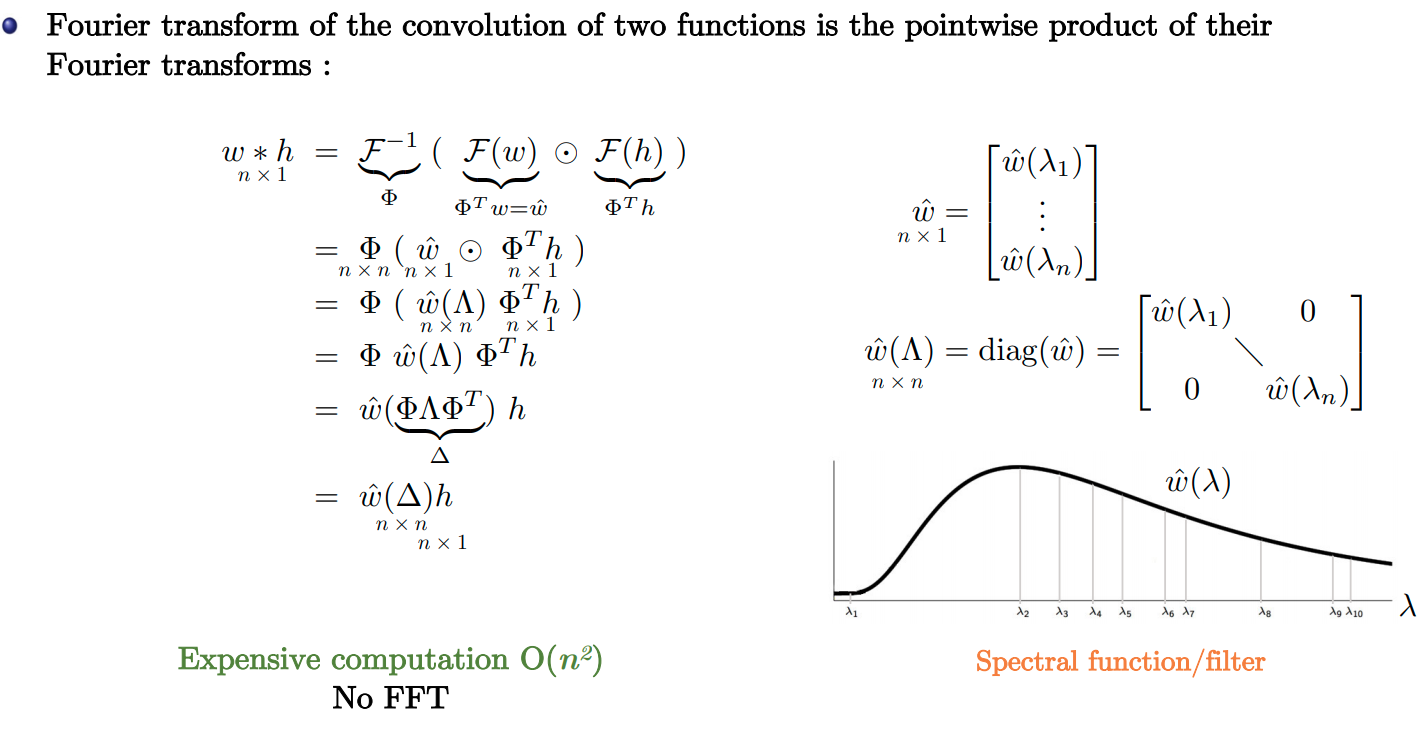
- Slide Credit: Xavier Bresson
No Shift Invariance for Graphs
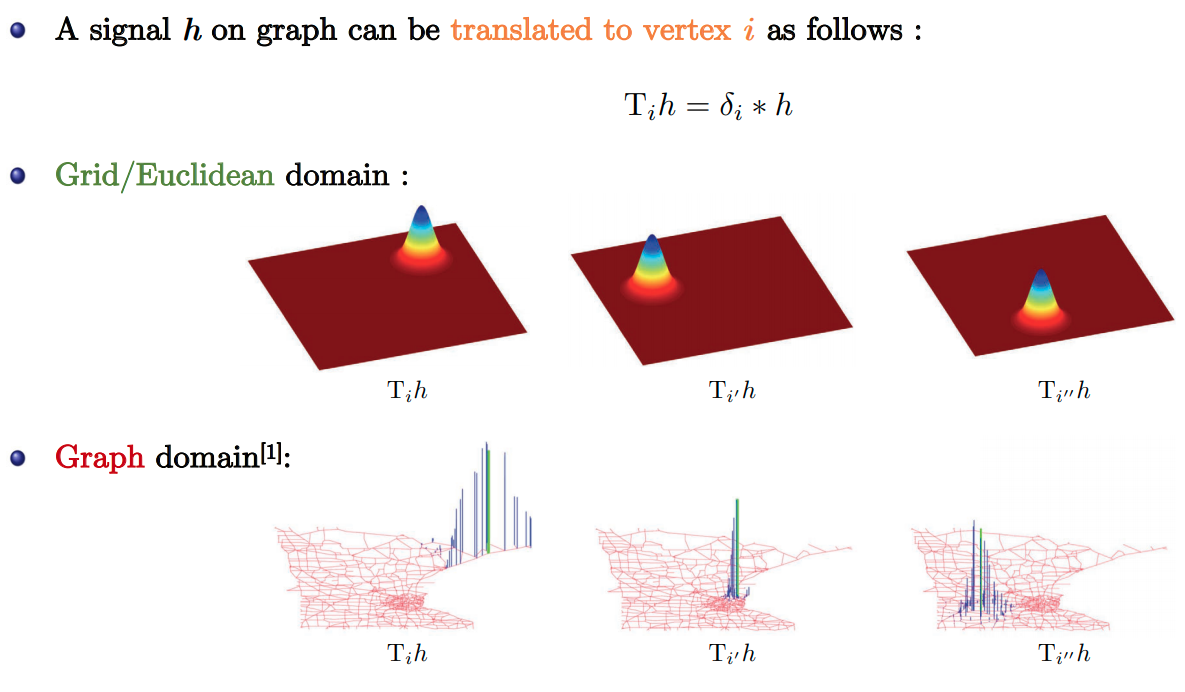
- Slide Credit: Xavier Bresson
Simple Spectral GCN
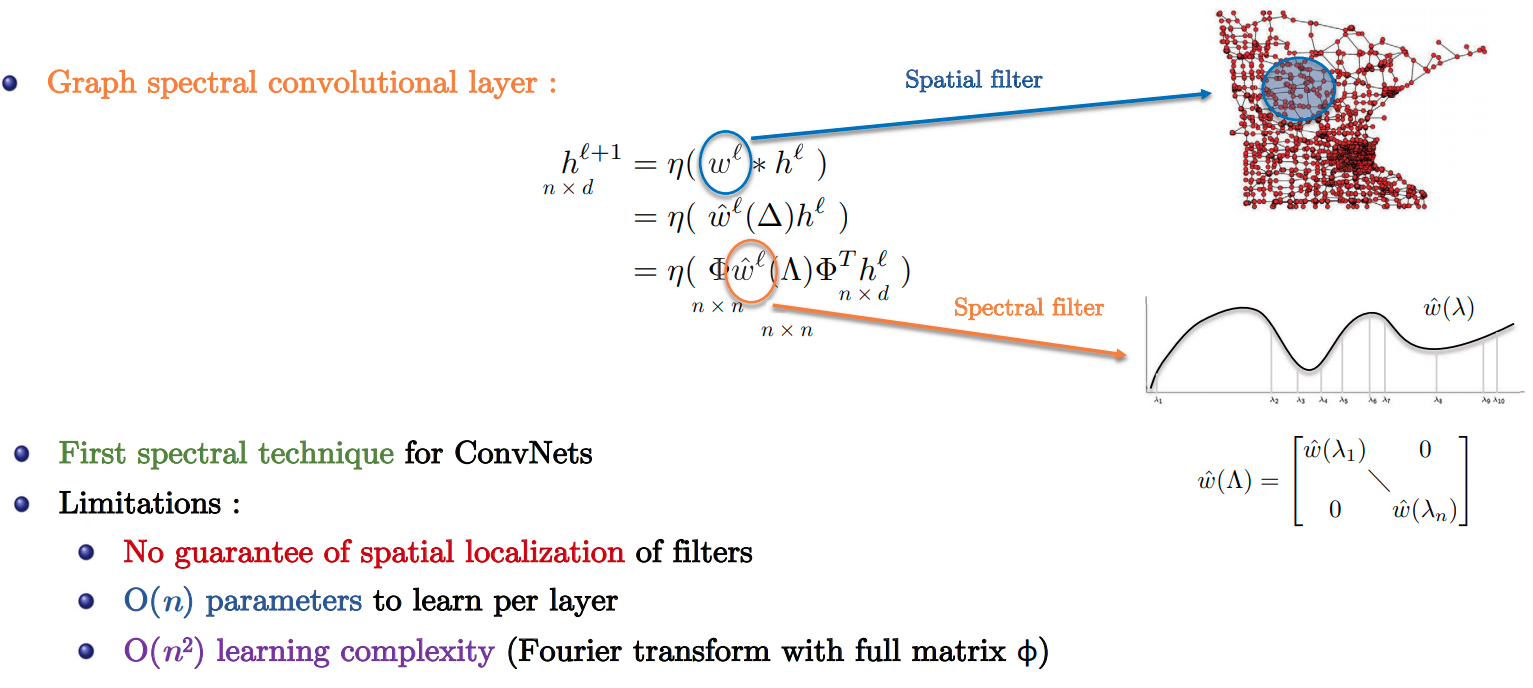
- Slide Credit: Xavier Bresson
Spline GCN

- Slide Credit: Xavier Bresson
LapGCN

- Slide Credit: Xavier Bresson
LapGCN

- Slide Credit: Xavier Bresson
LapGCN

- Slide Credit: Xavier Bresson
Chebyshev Polynomials

- Slide Credit: Xavier Bresson
MNIST Experiment
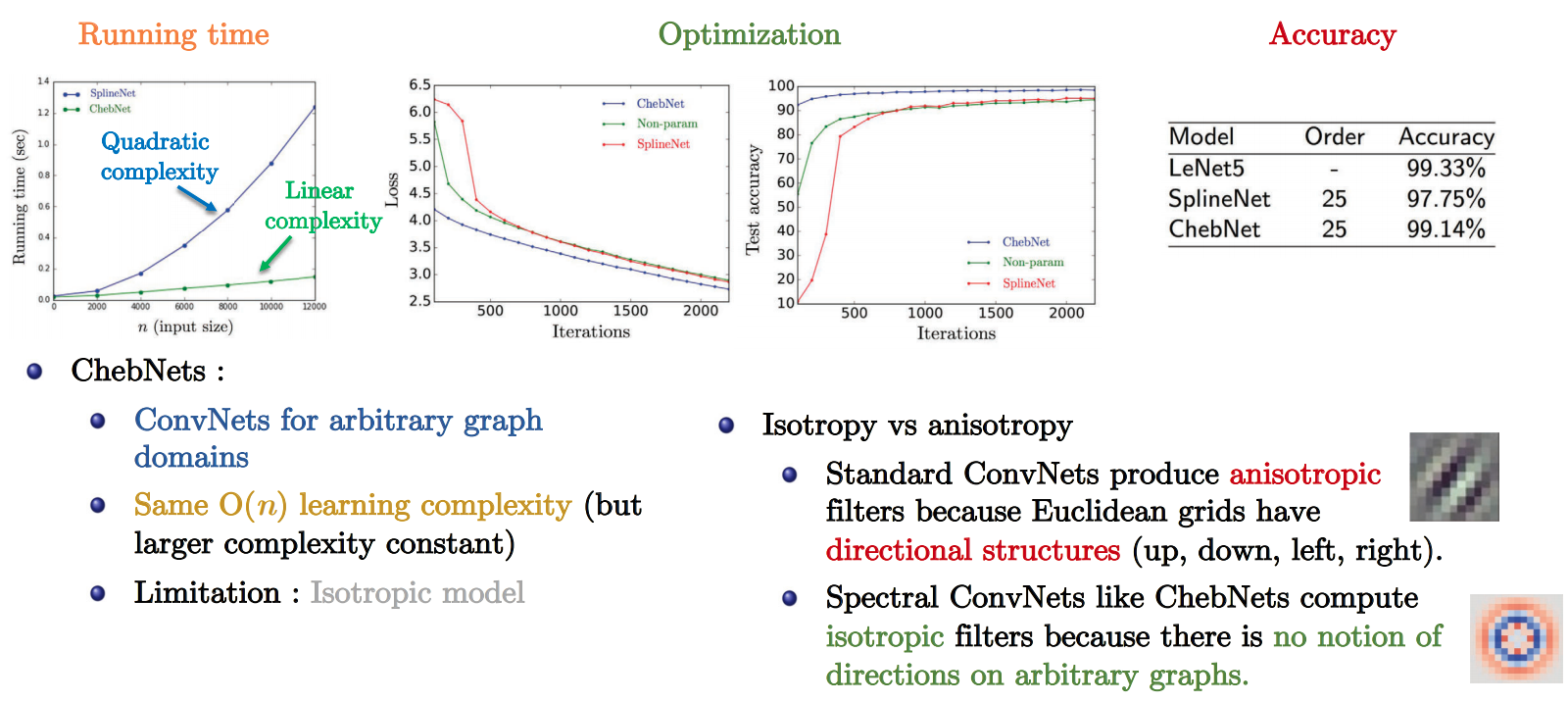
- Slide Credit: Xavier Bresson