Graph Neural Networks

Graph Neural Networks - II

CSE 891: Deep Learning

Vishnu Boddeti

Wednesday October 28, 2020

Recap: Graph Structured Data

Standard CNN and RNN architectures don't work on this data.

Slide Credit: Xavier Bresson

Recap: Graph Definition

Graphs $\mathcal{G}$ are defined by:

Vertices $V$
Edges $E$
Adjacency matrix $\mathbf{A}$

Features:

Node features: $\mathbf{h}_i, \mathbf{h}_j$ (user type)
Edge features: $\mathbf{e}_{ij}$ (relation type)
Graph features: $\mathbf{g}$ (network type)

Recap: Chebyshev Polynomials

Slide Credit: Xavier Bresson

Spatial Graph ConvNets

Template Matching

How to define template matching for graphs?

Main issue is the absence of node ordering/positioning.

Node indices are arbitrary and do not match the same information.

How to design template matching invariant to node re-parametrization ?

Simply use the same template features for all neighbors !

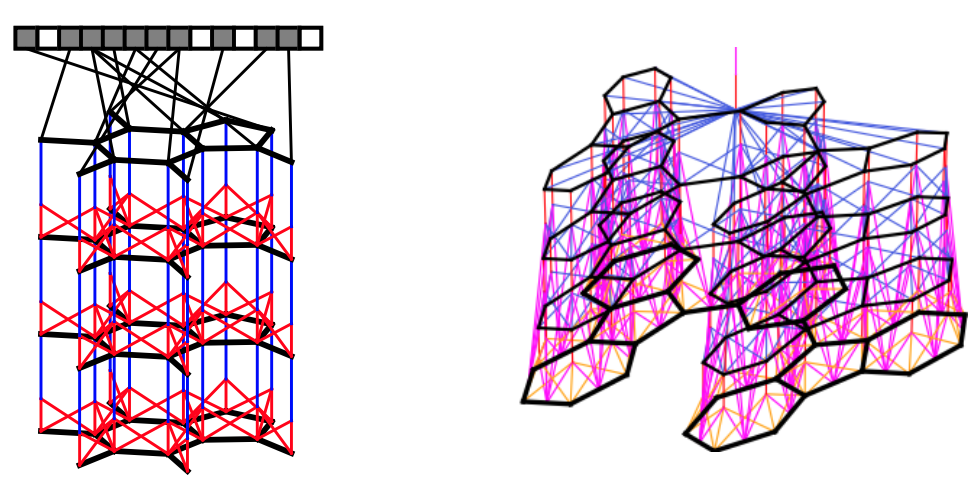
Message Passing Neural Networks

Use neural network to mimic unrolled message passing in graphs.

$\begin{eqnarray} \mathbf{m}_{i}^{t+1} &=& \sum_{j \in \mathcal{N}_i} M_t(h_i^t,h_j^t, e_{ij}) \\ \mathbf{h}_{i}^{t+1} &=& \sum_{j \in \mathcal{N}_i} U_t(h_i^{t},m_i^{t+1}) \\ \hat{y} &=& R(\{h^T_i | i \in \mathcal{G}\}) \\ \end{eqnarray}$

Figure Credit: David Duvenaud

Template Matching

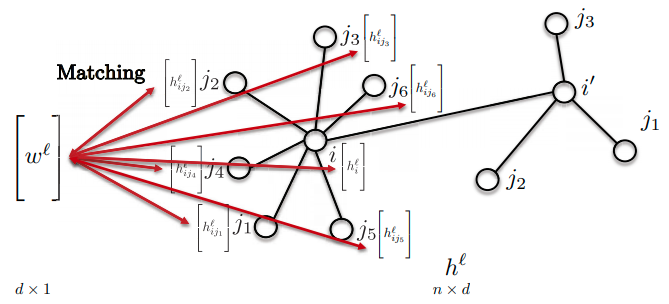
One Feature: $\begin{equation}h_i^{(l+1)}=\sigma\left(\sum_{j\in\mathcal{N}_i}(\mathbf{w}^l)^T \mathbf{h}^l_{ij}\right)\end{equation}$
$d$ Feature: $\begin{equation}\mathbf{h}_i^{(l+1)}=\sigma\left(\sum_{j\in\mathcal{N}_i}\mathbf{W}^l \mathbf{h}^l_{ij}\right)\end{equation}$
Vector Representation: $\begin{equation}\mathbf{h}_i^{(l+1)}=\sigma\left(\mathbf{A}\mathbf{h}^l\mathbf{W}^l\right)\end{equation}$

Figure Credit: Xavier Bresson

Vanilla Spatial GCN

Simplest formulation of spatial GCNs

Handle the absence of node ordering

Invariant by node re-parametrization

Deal with different neighborhood sizes
Local reception field by design (only neighbors are considered)
Weight sharing (convolution property)
Independent of graph size
Limited to isotropic capability

$\begin{equation}\mathbf{h}_i^{(l+1)}=\sigma\left(\mathbf{A}\mathbf{h}^l\mathbf{W}^l\right)\end{equation}$

$\begin{equation}\mathbf{h}_i^{(l+1)}=\sigma\left( \frac{1}{d_i} \sum_{j \in \mathcal{N}_i} A_{ij}\mathbf{W}^l\mathbf{h}^l_j\right)\end{equation}$

$\begin{equation}\mathbf{h}_i^{(l+1)}=f_{GCN}(\mathbf{h}_i^l,{\mathbf{h}_j^l:j\rightarrow i})\end{equation}$

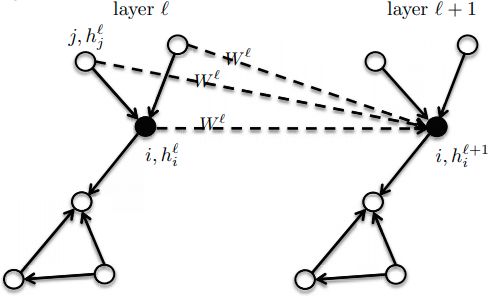
Figure Credit: Xavier Bresson

Graph Convolutional Networks

Figure Credit: Michael Bronstein

GCN Challenges

Small world graphs

Bottleneck Problem

Figure Credit: Michael Bronstein

GraphSage

Vanilla GCNs (supposing $A_{ij}$ = 1): $h_i^{(l+1)}=\sigma\left(\frac{1}{d_i}\sum_{j\in\mathcal{N}_i}W^lh^l_j\right)$
GraphSage:

Differentiate template weights $W^l$ between neighbors $h_j$ and central node $h_i$ .

$\begin{equation}\mathbf{h}_i^{(l+1)}=\sigma\left( \mathbf{W}^l_1\mathbf{h}^l_i + \frac{1}{d_i} \sum_{j \in \mathcal{N}_i} \mathbf{W}^l_2\mathbf{h}^l_j\right)\end{equation}$

Isotropic GCNs
Variations:

Instead of mean, use Max, LSTM etc.

GraphSage

How do we scale to large graphs?
Mini-Batch Training:

Samples are not IID anymore.
How do we sample?

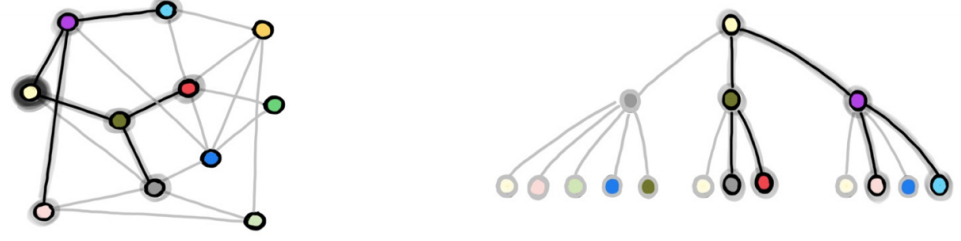
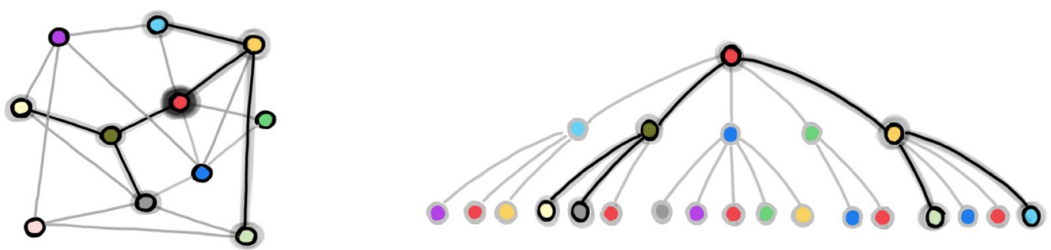
Figure Credit: Michael Bronstein

Graph Isomorphism Networks

Graph isomorphism is an equivalent relation for similar graph structures.
Architecture that can differentiate graphs that are not isomorphic.
Isotropic GCNs

$\begin{eqnarray} \mathbf{h}_i^{(l+1)} &=& ReLU \left( \mathbf{W}_2^l ReLU\left(BN\left(W_1^l\hat{h}_i^{l+1}\right)\right) \right) \\ \hat{h}_i^{l+1} &=& (1+\epsilon)h_i^l + \sum_{j\in\mathcal{N}_i}h_j^l \end{eqnarray}$

Anistropic GCNs

Reminder:

Standard ConvNets produce anisotropic filters because Euclidean grids have directional structures (up, down, left, right).
GCNs such as ChebNets, CayleyNets, Vanilla GCNs, GraphSage, GIN compute isotropic filters as there is no notion of directions on arbitrary graphs.

How to get anisotropy back in GNNs?

Natural edge features if available (e.g. different bond connections between atoms).
We need an anisotropic mechanism that is independent of the node parametrization.
Idea: Graph attention mechanism can treat neighbors differently.

Graph Attention Networks

GAT uses the attention mechanism to introduce anisotropy in the neighborhood aggregation function.
The network employs a multi-headed architecture to increase the learning capacity, similar to the Transformer.

$\begin{eqnarray} h_i^{l+1} &=& Concat_{k=1}^K(ELU(\sum_{j\in\mathcal{N}_i}\alpha_{ij}^{k,l}W_1^kh_j^l)) \\ \alpha_{ij}^{k,l} &=& Softmax_{\mathcal{N}_i}(\hat{\alpha}_{ij}^{k,l}) \\ \hat{\alpha}_{ij}^{k,l} &=& LeakyReLU(W_2^{k,l}Concat(W_1^{k,l}h_i^l,W_1^{k,l}h_j^l)) \end{eqnarray}$

Attention mechanism in a one-hop neighborhood

Graph Transformers

Graph version of Transformer:

$\begin{eqnarray} h_i^{l+1} &=& W^lConcat_{k=1}^K(\sum_{j\in\mathcal{N}_i}\alpha_{ij}^{k,l}V^{k,l}h_j^l) \\ \alpha_{ij}^{k,l} &=& Softmax_{\mathcal{N}_i}(\hat{\alpha}_{ij}^{k,l}) \\ \hat{\alpha}_{ij}^{k,l} &=& (Q^{l,k}h_i^l)^TK^{l,k}h_j^l \end{eqnarray}$

Attention mechanism in a on-hop neighborhood

Transformers

Transformers is a special case of GCNs when the graph is fully connected.
The neighborhood $\mathcal{N}_i$ is the whole graph.

Fully Connected Graph

$\begin{eqnarray} h_i^{l+1} &=& Concat_{k=1}^K(Softmax(Q^lK^{l^T})V^l)W^l \\ Q^l &=& h^lW^l_Q \\ K^l &=& h^lW^l_K \\ V^l &=& h^lW^l_V \\ \end{eqnarray}$

Transformers

What does it mean to have a graph fully connected?

It becomes less useful to talk about graphs as each data point is connected to all other points. There is no particular graph structure that can be used.
It would be better to talk about sets rather than graphs in this case.
Transformers are Set Neural Networks.

They are today the best technique to analyze sets/bags of features.

GNN Pipeline

Standard GNN Pipeline:

Input Layer: Linear embedding of input node/edge features.
GNN Layers: Apply favorite GNN layer $L$ times.
Task-based layer : Graph/node/edge prediction layer.

GNN Pipeline

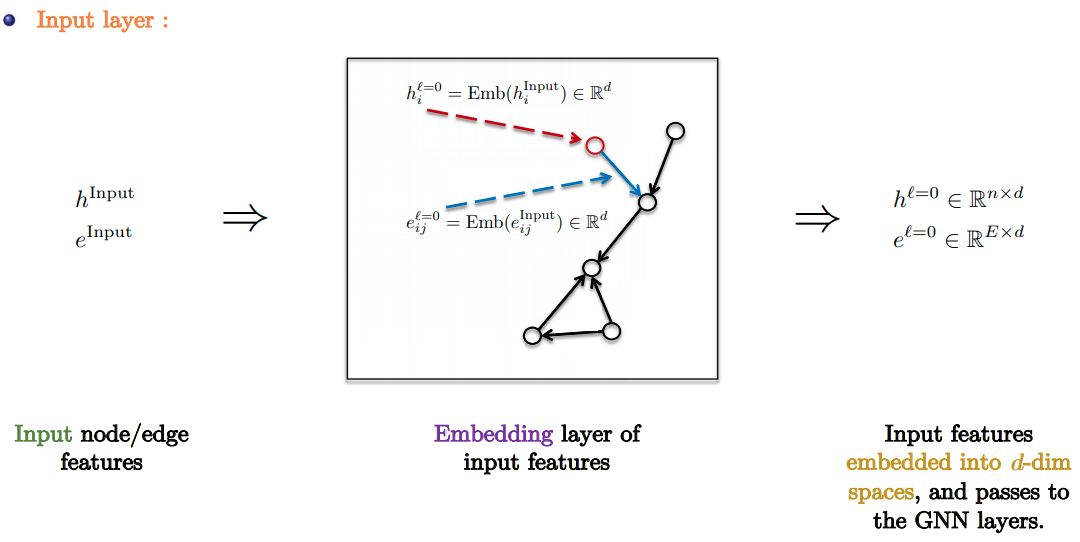
Slide Credit: Xavier Bresson

GNN Pipeline

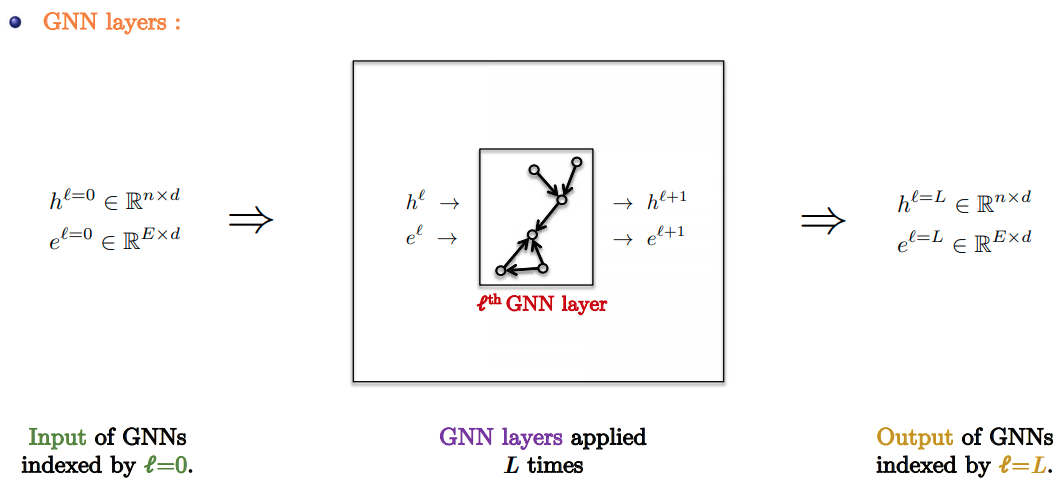
Slide Credit: Xavier Bresson

GNN Pipeline

Slide Credit: Xavier Bresson

Node Classification

Figure Credit: Jure Leskovec

Link Prediction

Figure Credit: Jure Leskovec

Social Networks

Figure Credit: Michael Bronstein

Social Networks

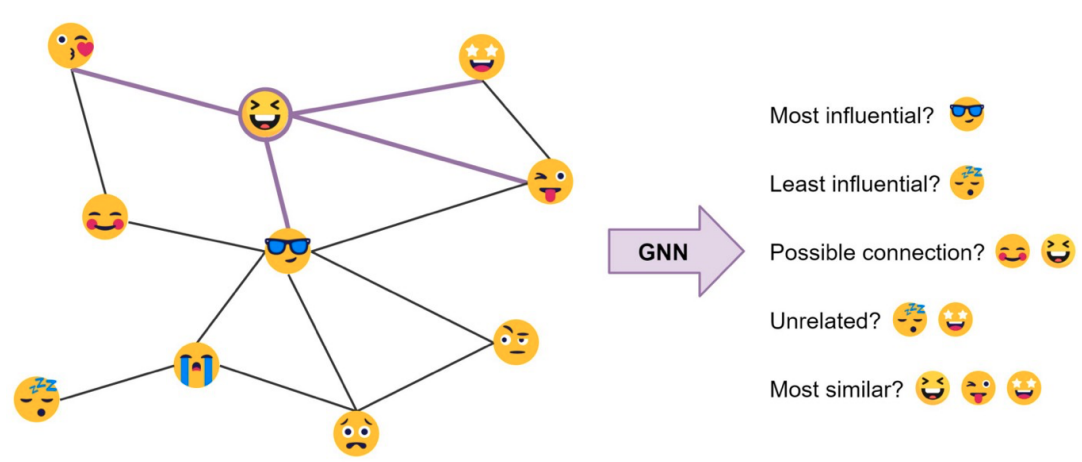
Figure Credit: Chaitanya Joshi

Quantum Chemistry

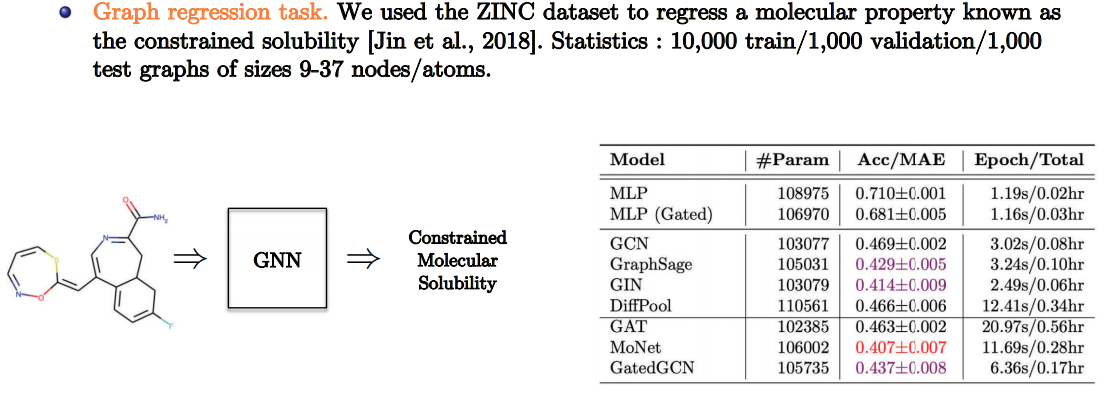
Slide Credit: Xavier Bresson

Computer Vision

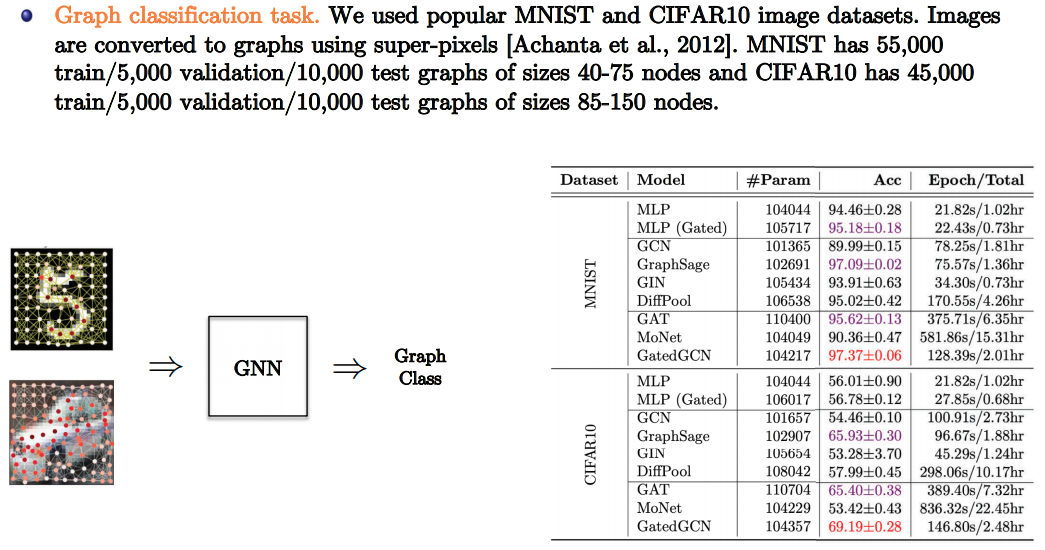
Slide Credit: Xavier Bresson

Combinatorial Optimization

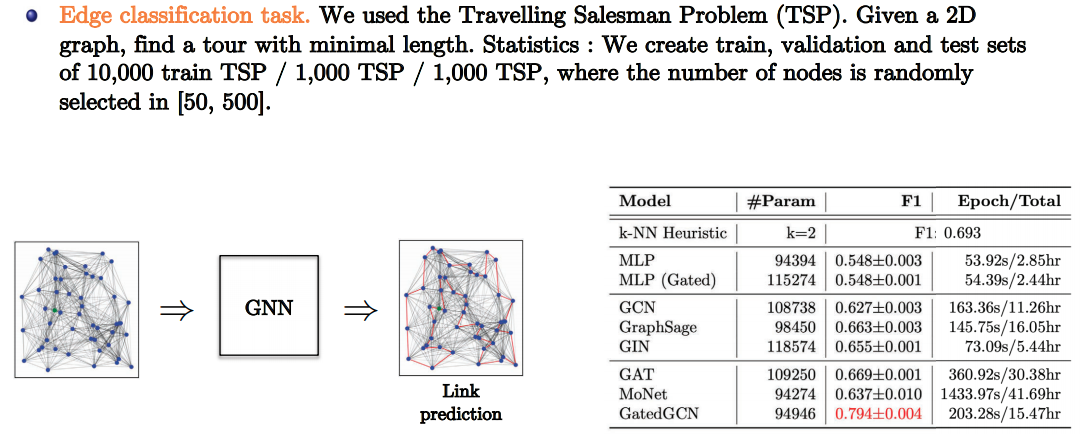
Slide Credit: Xavier Bresson

Graph Classification

Duvenaud et.al "Convolutional Networks on Graphs for Learning Molecular Fingerprints", NeurIPS 2015

Semi-Supervised Classification on Graphs

Setting:

Some nodes are labeled
All other nodes are unlabeled

Task:

Predict node label of unlabeled nodes

Evaluate loss on labeled nodes only:

$\begin{equation} \mathcal{L} = -\sum_{l\in\mathcal{Y}_L}\sum_{f=1}^F Y_lf \log Z_lf \end{equation}$

$\mathcal{Y}_L$ : set of labled node indices
$\mathbf{Y}$ : label matrix
$\mathbf{Z}$ : GCN output (after softmax)

Normalization and Depth

What kind of normalization can we do for graphs?

Node normalization
Pair normalization
Edge normalization

Does depth matter for GCNs?

Scalable Inception Graph Neural Networks

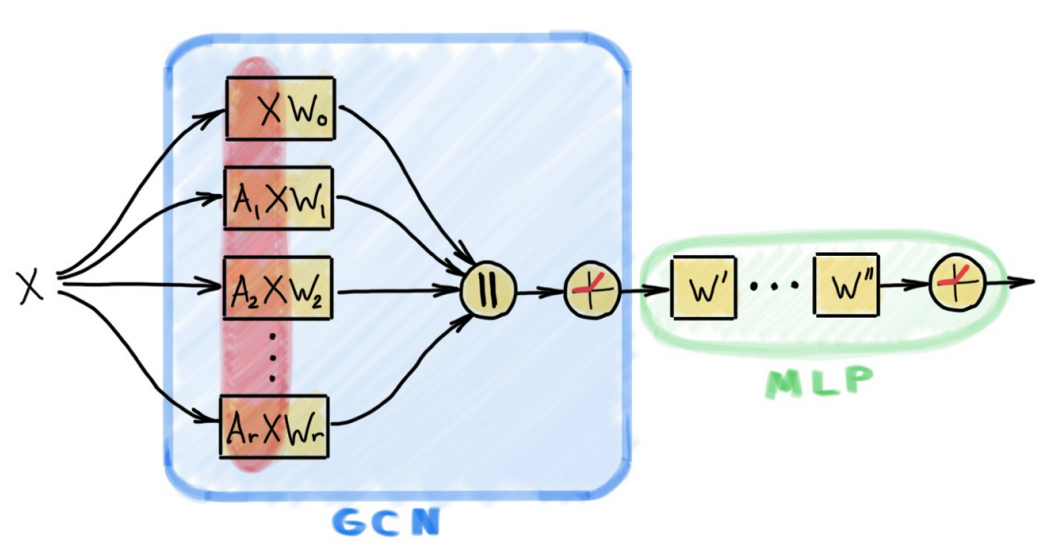
Figure Credit: Michael Bronstein

Scalable Inception Graph Neural Networks

Graph CNN Challenges

How to define compositionality on graphs (i.e. convolution, downsampling, and pooling on graphs)?
How to ensure generalizability across graphs?
And how to make them numerically fast? (as standard CNNs)
Scalability: millions of node, billions of edges
How to process dynamic graphs?
How to incorporate higher-order structures?
How powerful are graph neural networks?

limited theoretical understanding
message passing based GCN are no stronger than Weisfeiler-Lehman tests.

Getting Started

Lots of open questions and uncharted territory.
Standardized Benchmarks: Open Graph Benchmark
Software Packages: Pytorch Geometric or Deep Graph Library

Summary

Generalization of ConvNets to data on graphs
Re-design convolution operator on graphs
Linear complexity for sparse graphs
GPU implementations exist, but not yet optimized for sparse matrix-matrix multiplications.
Spatial GCN is usually more efficient but less principled.
Spectral GCN is more principled but usually slow. Computing Laplacian eigenvectors for large scale data is painful.

Recap: Graph Structured Data

Recap: Graph Definition

Recap: Chebyshev Polynomials

Isotropic Filters

Spatial Graph ConvNets

Template Matching

Template Matching

Vanilla Spatial GCN

Graph Convolutional Networks

GCN Challenges

GraphSage

GraphSage

Graph Isomorphism Networks

Anistropic GCNs

Graph Attention Networks

Graph Transformers

Transformers

Transformers

Applications

GNN Pipeline

GNN Pipeline

GNN Pipeline

GNN Pipeline

Node Classification

Link Prediction

Social Networks

Social Networks

Quantum Chemistry

Computer Vision

Combinatorial Optimization

Graph Classification

Semi-Supervised Classification on Graphs

Normalization and Depth

Scalable Inception Graph Neural Networks

Scalable Inception Graph Neural Networks

Graph CNN Challenges

Getting Started

Summary

Q & A