Generative Models - Introduction

CSE 891: Deep Learning

Vishnu Boddeti

Monday November 09, 2020

Generative Models

• Unsupervised Learning: only use the inputs $\mathbf{x}^{(t)}$ for learning.
• automatically extract meaningful features for your data
• leverage the availability of unlabeled data
• add a data-dependent regularizer to trainings
• We will see 4 neural network based approaches for unsupervised learning
• Autoregressive Models
• Autoencoders (Variational Autoencoders)
• Generative Adversarial Networks
• Normalizing Flows

Why Generative Models?

• Move beyond associating inputs to outputs
• Recognize objects in the world and their factors of variation
• Understand and imagine how the world evolves
• Detect surprising events in the world
• Imagine and generate rich plans for the future
• Establish concepts as useful for reasoning and decision making

Desiderata

• We want to estimate distributions of complex, high-dimensional data
• A $128\times 128\times 3$ image lies in a ~50,000-dimensional space
• We also want computational and statistical efficiency
• Efficient training and model representation
• Expressiveness and generalization
• Sampling quality and speed
• Compression rate and speed

Simplest Generative Model

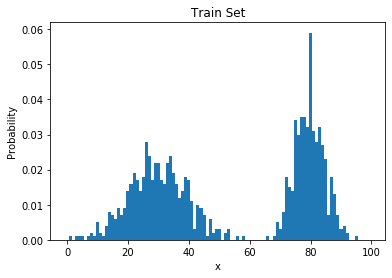
Learning Through Histograms

Inference and Sampling

• Inference (querying $p_i$ for arbitrary $i$): simply a lookup into the array $p_1, \dots, p_k$
• Sampling (lookup into the inverse cumulative distribution function)
• From the model probabilities $p_1, \dots, p_k$, compute the cumulative distribution
• Draw a uniform random number $u \sim [0, 1]$
• Return the smallest $i$ such that $u \leq F_i$
• Are we done?

Failure in High Dimensions

• No, because of the curse of dimensionality. Counting fails when there are too many bins.
• (Binary) MNIST: 28x28 images, each pixel in {0, 1}
• There are $2^{784} \approx 10^{236}$ probabilities to estimate
• Any reasonable training set covers only a tiny fraction of this
• Each image influences only one parameter. No generalization whatsoever!

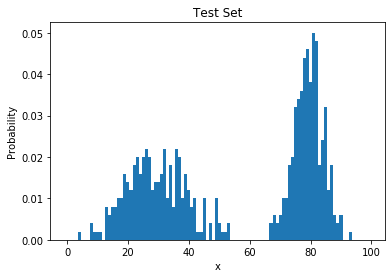
Poor Generalization

• learned histogram = training data distribution
• poor generalization

Parameterized Distributions

Status

• Issues with Histograms
• High dimensions: won't work
• Even 1-d: if many values in the domain, prone to overfitting
• Solution: function approximation. Instead of storing each probability, store a parameterized function $p_{\mathbf{\theta}}(\mathbf{x})$

Applications

Applications: Data Generation

Applications: Data Generation

Applications: Data Imputation, Denoising, In-painting

Applications: Communication and Compression

Learning Generative Models

Likelihood-based generative models

• Our goal: estimate $p_{data}$ from samples $x^{(1)}, \dots, x^{(n)} \sim p_{data}(x)$
• Now we introduce function approximation: learn $\mathbf{\theta}$ so that $p_{\mathbf{\theta}}(x) \approx p_{data}(x)$
• How do we design function approximators to effectively represent complex joint distributions over $\mathbf{x}$, yet remain easy to train?
• There will be many choices for model design, each with different trade-offs and different compatibility criteria.
• Designing the model and the training procedure go hand-in-hand.

Fitting Distributions

• Given data $x^{(1)}, \dots, x^{(n)}$ sampled from a "true" distribution $p_{data}$
• Set up a model class: a set of parameterized distributions $p_{\mathbf{\theta}}$
• Pose a search problem over parameters $$\begin{equation} \underset{\mathbf{\theta}}{\operatorname{arg min}} loss(\mathbf{\theta},\mathbf{x}^{(1)}, \dots, \mathbf{x}^{(n)}) \end{equation}$$
• Want the loss function + search procedure to:
• Work with large datasets ($n$ is large, say millions of training examples)
• Yield $\mathbf{\theta}$ such that $p_{\mathbf{\theta}}$ matches $p_{data}$ - i.e. the training algorithm works. Think of the loss as a distance between distributions.
• Note that the training procedure can only see the empirical data distribution, not the true data distribution: we want the model to generalize.

Maximum Likelihood

• Maximum likelihood: given a dataset $x^{(1)}, \dots, x^{(n)}$, find $\mathbf{\theta}$ by solving the optimization problem
$$\begin{equation} \underset{\mathbf{\theta}}{\operatorname{arg min}} loss(\mathbf{\theta},\mathbf{x}^{(1)}, \dots, \mathbf{x}^{(n)}) = \frac{1}{n}\sum_{i=1}^n -\log p_{\mathbf{\theta}}(\mathbf{x}^{(i)}) \end{equation}$$
• Statistics tells us that if the model family is expressive enough and if enough data is given, then solving the maximum likelihood problem will yield parameters that generate the data
• Equivalent to minimizing KL divergence between the empirical data distribution and the model $$\begin{eqnarray} \hat{p}_{data}(\mathbf{x}) &=& \frac{1}{n}\sum_{i=1}^n\mathbf{1}[\mathbf{x}==\mathbf{x}^{(i)}] \\ KL(\hat{p}_{data}||p_{\mathbf{\theta}}) &=& \mathbb{E}_{\mathbf{x}\sim\hat{p}_{data}}[-\log p_{\mathbf{\theta}}(\mathbf{x})] - H(\hat{p}_{data}) \end{eqnarray}$$

Stochastic Gradient Descent

• Maximum likelihood is an optimization problem. How do we solve it?
• Stochastic gradient descent (SGD).
• SGD minimizes expectations: for f a differentiable function of θ, it solves $$\begin{equation} \underset{\mathbf{\theta}}{\operatorname{arg min}} \mathbb{E}[f(\mathbf{\theta})] \end{equation}$$
• With maximum likelihood, the optimization problem is $$\begin{equation} \underset{\mathbf{\theta}}{\operatorname{arg min}} \mathbb{E}_{\mathbf{x}\sim\hat{p}_{data}}[-\log p_{\mathbf{\theta}}(\mathbf{x})] \end{equation}$$
• Why maximum likelihood + SGD? It works with large datasets and is compatible with neural networks.

Designing The Model

• Key requirement for maximum likelihood + SGD: efficiently compute $\log p(x)$ and its gradient
• We will choose models $p_{\mathbf{\theta}}$ to be deep neural networks, which work in the regime of high expressiveness and efficient computation (assuming specialized hardware)
• How exactly do we design these networks?
• Any setting of $\mathbf{\theta}$ must define a valid probability distribution over $\mathbf{x}$: $$\begin{equation} \mbox{for all } \mathbf{\theta}, \mbox{ } \sum_{\mathbf{x}}p_{\mathbf{\theta}}(\mathbf{x}) = 1 \mbox{ and } p_{\mathbf{\theta}}(\mathbf{x})\geq 0 \mbox{ for all } \mathbf{x} \end{equation}$$
• $\log p_{\mathbf{\theta}}(\mathbf{x})$ should be easy to evaluate and differentiate with respect to $\mathbf{\theta}$
• This can be tricky to set up!

Simple Generative Models

Example: Autoencoder

• Autoencoders consists of:
• encoder
• decoder
• Encoder and decoder are trained to reproduce its input at the output layer.

Loss Function

• Binary Inputs
• cross-entropy \begin{equation} L = -\sum_{k} x_k\log(\hat{x}_k) + (1-x_k)\log(1-\hat{x}_k) \nonumber \end{equation}
• Real-Valued Inputs
• sum-of-squared differences
• we use a linear activation function at the output \begin{equation} L = \frac{1}{2}\sum_{k}(x_k-\hat{x}_k)^2 \nonumber \end{equation}
• Gradient: $\nabla_{\mathbf{\hat{a}}(\mathbf{x}^{t})}L = \mathbf{\hat{x}}^{t} - \mathbf{x}^{t}$
• when weights are tied, $\nabla_{\mathbf{W}}L$ is the sum of two gradients.

Under-complete Hidden Layers

• Training Distribution:

• Other Distribution:

Over-complete Hidden Layer

Denoising Autoencoder

Linear Autoencoder

• Given a linear decoder, what is the best encoder for MSE loss?
• Theorem:
• let $\mathbf{A}$ be any matrix, with SVD $\mathbf{A}=\mathbf{U\Sigma V}^T$
• Decomposition of rank $K$: $\mathbf{U}_{.,\leq K}\Sigma_{\leq K, \leq K}\mathbf{V}^T_{.,\leq K}$
• then, the matrix $\mathbf{B}$ of rank $K$ that is closest to $\mathbf{A}$: \[\mathbf{B}^{*} = \underset{\mathbf{B} \mbox{ s.t. rank}(\mathbf{B})=K}{\operatorname{arg min}} \|A-B\|_{F}\] is $\mathbf{B}^{*}=\mathbf{U}_{.,\leq K}\Sigma_{\leq K, \leq K}\mathbf{V}^T_{.,\leq K}$
• If inputs are normalized as follows: $\mathbf{x}^t = \frac{1}{\sqrt{T}}\left(\mathbf{x}^t-\frac{1}{T}\sum_{t'=1}^T\mathbf{x}^{t'}\right)$
• encoder corresponds to Principal Component Analysis (PCA)
• singular values and (left) vectors = the eigenvalues/eigenvectors of covariance matrix

What you will learn

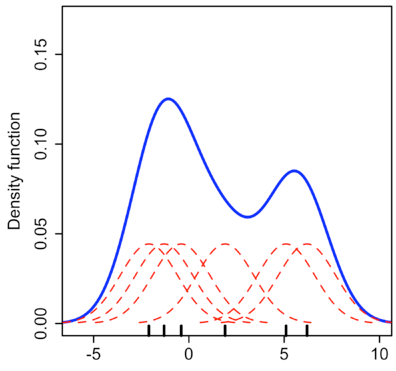
A Probabilistic Viewpoint

• Goal: modeling $p_{data}$

Fully Observed Models

Transformation Models (likelihood free)

Latent Variable Models (observation noise)

Undirected Latent Variable Models (hidden factors)