Generative Adversarial Networks

CSE 891: Deep Learning

Vishnu Boddeti

Wednesday November 25, 2020

A Probabilistic Viewpoint

Goal: modeling $p_{data}$

Fully Observed Models

Transformation Models (likelihood free)

Latent Variable Models (observation noise)

Undirected Latent Variable Models (hidden factors)

Overview

One way to judge the quality of a generative model is to sample from it.
This field has seen rapid progress:

Implicit Generative Models

Implicit generative models implicitly define a probability distribution
Start by sampling the code vector z from a fixed, simple distribution (e.g. spherical Gaussian)
The generator network computes a differentiable function $G$ mapping $\mathbf{z}$ to an $\mathbf{x}$ in data space

Implicit Generative Models: 1-D Example

Generative Adversarial Networks

Implicit generative models: if there is a criterion for evaluating the quality of samples, one can compute its gradient with respect to the network parameters, and update the network's parameters to improve the quality of the sample.
Generative Adversarial Networks (GANs): train two different networks

Generator Network: tries to produce realistic-looking samples
Discriminator Network: tries to figure out whether an image came from the training set or the generator network

The goal of the generator network it to fool the discriminator network.

Generative Adversarial Networks

Let $D$ be the discriminator's probability of being real data.
Discriminator's Loss: cross-entropy for binary classification between real and fake data. \begin{equation} J_D = \mathbb{E}_{\mathbf{x}}[-\log D(x)] + \mathbb{E}_{\mathbf{z}}[-\log(1-D(G(\mathbf{z})))] \end{equation}
A plausible cost function for the generator: the opposite of the discriminator \begin{equation} \begin{aligned} J_G &= -J_D \\ &= \mathbb{E}_{\mathbf{z}}[\log(1-D(G(\mathbf{z})))] \end{aligned} \end{equation}
This is called a minimax formulation, since the generator and discriminator are playing a zero-sum game against each other. \begin{equation} \max_{G}\min_D J_D \end{equation}

Generative Adversarial Networks

$\mathcal{F}(\mathbf{x},\theta, \phi) = \mathbb{E}_{p(x^{obs})}[\log D_{\theta}(\mathbf{x}^{obs})] + \mathbb{E}_{p(z)}[\log (1-D_{\theta}(f_{\phi}(z)))]$

\begin{eqnarray} \mathbf{z} &\sim& p(\mathbf{z}) \nonumber \\ \mathbf{x}^{gen} &=& f_{\phi}(\mathbf{z}) \nonumber \end{eqnarray}

Alternating Minimization: \begin{equation} \min_{\phi}\max_{\theta} \mathcal{F}(\mathbf{x},\theta,\phi) \nonumber \end{equation}
Step 1 (update $D$): $\mathbf{\theta} = \mathbf{\theta} + \alpha_\mathbf{\theta} \frac{\partial \mathcal{F}(\mathbf{x},\theta, \phi)}{\partial \mathbf{\theta}}$
Step 2 (update $G$): $\mathbf{\phi} = \mathbf{\phi} + \alpha_\mathbf{\phi} \frac{\partial \mathcal{F}(\mathbf{x},\phi, \phi)}{\partial \mathbf{\phi}}$
We are not minimizing any overall loss! No training curves to look at!

Generative Adversarial Networks

Updating the Discriminator:

Generative Adversarial Networks

Updating the Generator:

Generative Adversarial Networks

Alternating Training of Generator and Discriminator:

A Better Loss Function

Original Loss Function: \begin{equation} J_G = \mathbb{E}_{\mathbf{z}}[\log(1-D(G(\mathbf{z})))]\nonumber \end{equation}

Right now $G$ is trained to minimize $\log(1-D(G(\mathbf{z}))$
At start of training, generator is very bad and discriminator can easily tell apart real/fake, so $D(G(\mathbf{z}))$ close to 0.
Problem: vanishing gradient for $G$

Modified Loss Function: \begin{equation} J_G = \mathbb{E}_{\mathbf{z}}[\log(-D(G(\mathbf{z})))]\nonumber \end{equation}

Instead, train $G$ to minimize $–\log(D(G(\mathbf{z}))$. Then $G$ gets strong gradients at start of training!
Fixes the saturation problem

Distance Metrics for Adversarial Networks

Total variation: $\delta(P_r, P_g) = \sup_{x}|P_r(x)-P_g(x)|$
KL Divergence: $KL(P_r\|P_g) = \int\log\left(\frac{P_r(x)}{P_g(x)}\right)P_r(x)dx$
Jenson-Shannon Divergence: $JS(P_r, P_g) = KL\left(P_r\|\frac{P_g+P_r}{2}\right) + KL\left(P_g\|\frac{P_r(x)+P_g(x)}{2}\right)$
Earth-Mover Distance (or Wasserstein-1): $W(P_r, P_g) = \inf_{\gamma\in\prod(P_r,P_g)}\mathbb{E}_{(x,y)\sim \gamma}[\|x-y\|]$

Generative Adversarial Networks

Since GANs were introduced in 2014, there have been thousands of papers introducing various architectures and training methods.
Most modern architectures are based on the Deep Convolutional GAN (DCGAN), where the generator and discriminator are both convolutional networks.
GAN Zoo

GAN Improvements: High Resolution

Celebrity Faces: $1024\times 1024$

Karras, Tero, Timo Aila, Samuli Laine, and Jaakko Lehtinen. "Progressive growing of gans for improved quality, stability, and variation." ICLR 2018

GAN Improvements: High Resolution

Bedrooms: $256\times 256$

Karras, Tero, Timo Aila, Samuli Laine, and Jaakko Lehtinen. "Progressive growing of gans for improved quality, stability, and variation." ICLR 2018

GAN Improvements: High Resolution

Objects: $256\times 256$

Karras, Tero, Timo Aila, Samuli Laine, and Jaakko Lehtinen. "Progressive growing of gans for improved quality, stability, and variation." ICLR 2018

GAN Improvements: High Resolution

Karras et.al, "A Style-Based Generator Architecture for Generative Adversarial Networks" CVPR 2019

Current State-of-the-Art: StyleGAN2

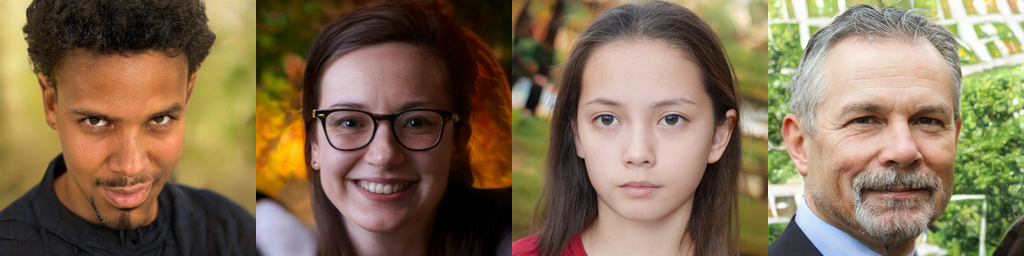
Karras et al, “Analyzing and Improving the Image Quality of StyleGAN”, CVPR 2020

Conditional GANs

Conditional Generative Models learn $p(x|y)$ instead of $p(x)$
Make generator and discriminator both take label y as an additional input!

Conditional GANs: Conditional Batch Normalization

Batch Normalization \begin{eqnarray} \mu_j &=& \frac{1}{N}\sum_{i=1}^N x_{i,j} \\ \sigma^2_j &=& \frac{1}{N}\sum_{i=1}^N (x_{i,j}-\mu_j)^2\\ \hat{x}_{i,j} &=& \frac{x_{i,j}-\mu_j}{\sqrt{\sigma^2_j+\epsilon}}\\ y_{i,j} &=& \gamma_j\hat{x}_{i,j}+\beta_j \end{eqnarray}

Conditional Batch Normalization \begin{eqnarray} \mu_j &=& \frac{1}{N}\sum_{i=1}^N x_{i,j}\\ \sigma^2_j &=& \frac{1}{N}\sum_{i=1}^N (x_{i,j}-\mu_j)^2\\ \hat{x}_{i,j} &=& \frac{x_{i,j}-\mu_j}{\sqrt{\sigma^2_j+\epsilon}}\\ y_{i,j} &=& \gamma_j^{\color{orange}y}\hat{x}_{i,j}+\beta_j^{\color{orange}y} \end{eqnarray}

Conditional GANs: Spectral Normalization

Welsh Springer Spaniel

Fire Truck

Daisy

Miyato et al, "Spectral Normalization for Generative Adversarial Networks", ICLR 2018

Conditional GAN: Self-Attention

Zhang et al, "Self-Attention Generative Adversarial Networks", ICML 2019

Conditional GAN: BigGAN

A Brock, J Donahue, K Simonyan, "Large Scale GAN Training for High Fidelity Natural Image Synthesis", ICLR 2019

Generating Videos with GANs

Clark et al, "Adversarial Video Generation on Complex Datasets", arXiv 2019

Conditioning on more than labels! Text to Image

Zhang et al, “StackGAN++: Realistic Image Synthesis with Stacked Generative Adversarial Networks.”, TPAMI 2018
Zhang et al, “StackGAN: Text to Photo-realistic Image Synthesis with Stacked Generative Adversarial Networks.”, ICCV 2017
Reed et al, “Generative Adversarial Text-to-Image Synthesis”, ICML 2016

Image Super-Resolution: Low-Res to High-Res

Ledig et al, "Photo-Realistic Single Image Super-Resolution Using a Generative Adversarial Network", CVPR 2017

Image-to-Image Translation: Pix2Pix

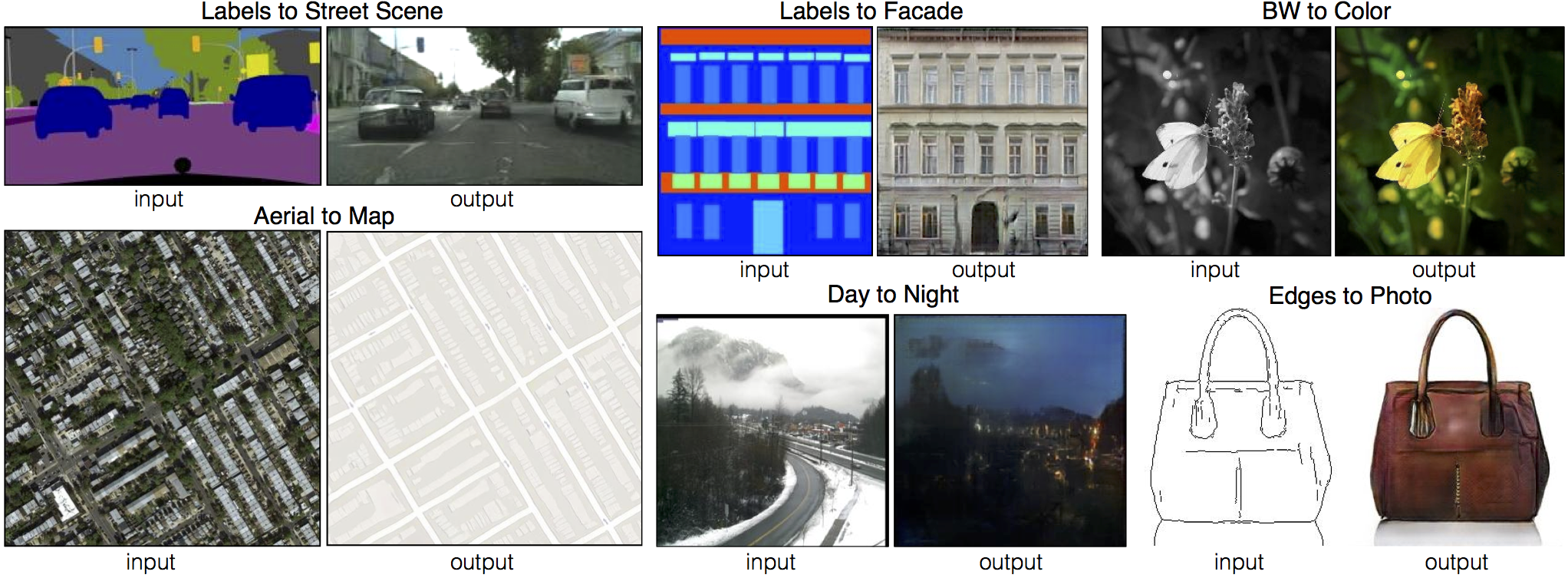
Isola et al, "Image-to-Image Translation with Conditional Adversarial Nets", CVPR 2017

CycleGAN

Style Transfer: change style while preserving content

Zhu et al, "Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks", ICCV 2017

CycleGAN

If we had paired data (same content in both styles), this would be a supervised learning problem. But this is hard to find.
The CycleGAN architecture learns to do it from unpaired data.

Train two different generators to go from style 1 to style 2, and vice versa.
Make sure the generated samples of style 2 are indistinguishable from real images by a discriminator net.
Make sure the generators are cycle-consistent: mapping from style 1 to style 2 and back again should give you almost the original image.

Zhu et al, "Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks", ICCV 2017

CycleGAN

Zhu et al, "Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks", ICCV 2017

CycleGAN

Style transfer between aerial images and maps

Zhu et al, "Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks", ICCV 2017

CycleGAN

Style transfer between roads scenes and semantic segmentation

Zhu et al, "Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks", ICCV 2017

Unpaired Image-to-Image Translation: CycleGAN

Zhu et al, "Unpaired Image-to-Image Translation using Cycle-Consistent Adversarial Networks", ICCV 2017

Label Map to Image

Park et al, "Semantic Image Synthesis with Spatially-Adaptive Normalization", CVPR 2019

Modern GAN Tricks

Self-Attention in Generator
Hinge Loss for Discriminator
Class conditional information
Spectral Normalization in generator
Update discriminator more than generator
Moving average of generator weights

Orthogonal weight initialization
Large batch size
Bigger models
Skip $\mathbf{z}$ connections
Orthogonal regularization
Truncation Trick

Do GANs Really Learn Distributions

GANs revolutionized generative modeling by producing crisp, high-resolution images.
The catch: do not seem to be modeling the distribution at all.

Cannot measure the log-likelihood they assign to held-out data.
Are they be memorizing training examples?
No way to tell if they are dropping important modes from the distribution.

Do GANs Really Learn Distributions

Equilibrium: may not exist
Convergence: Optimization problem is concave-concave even for simple instantiations

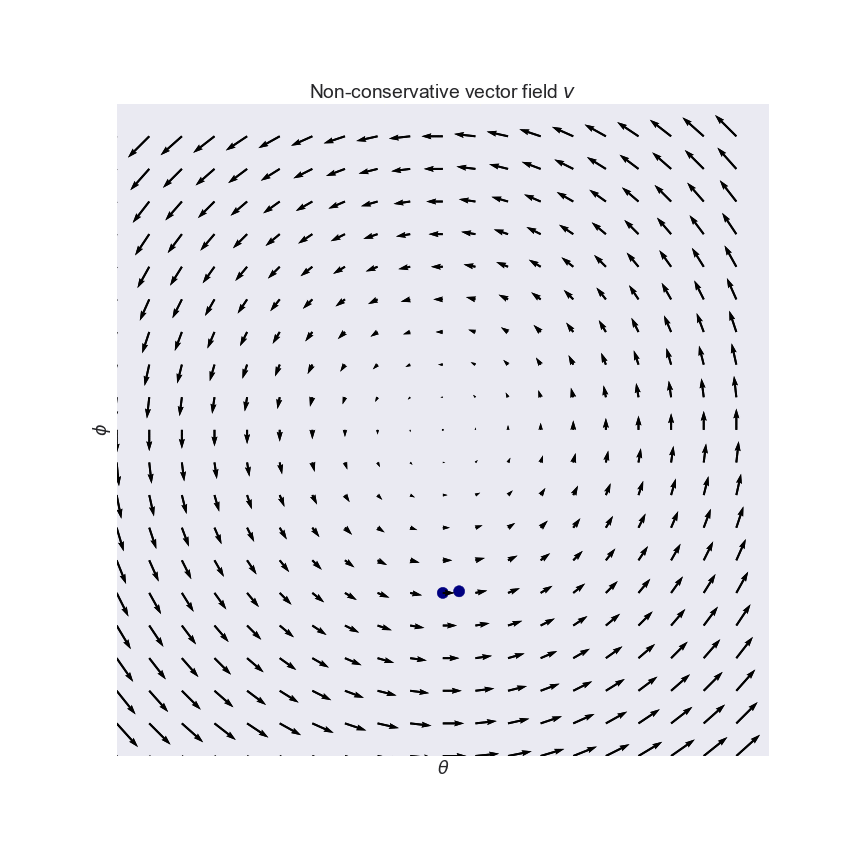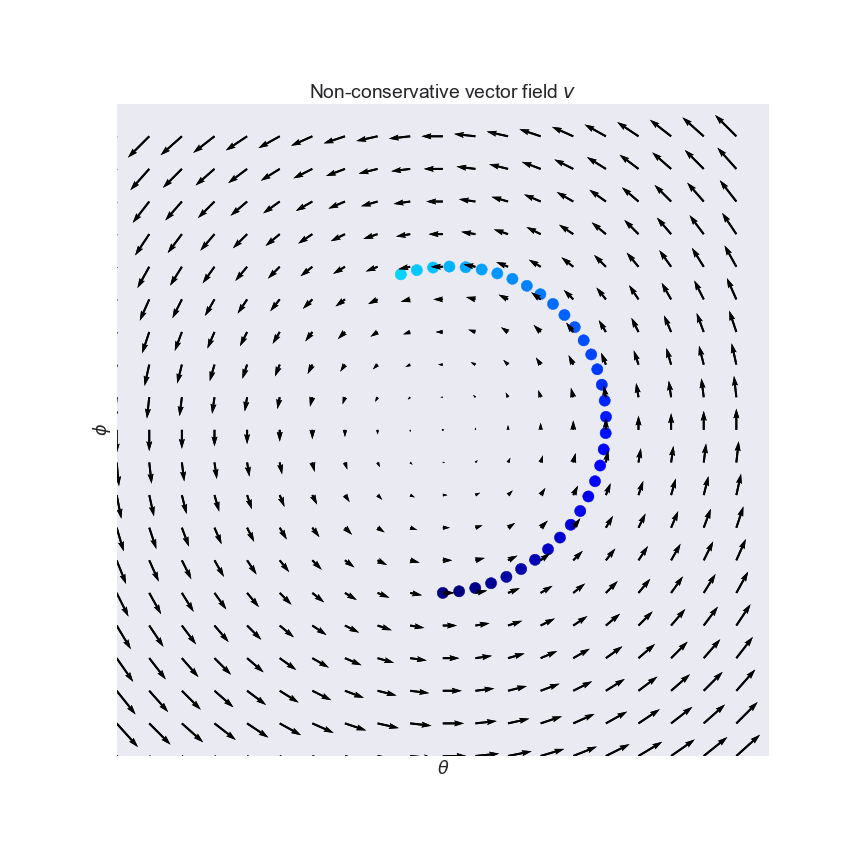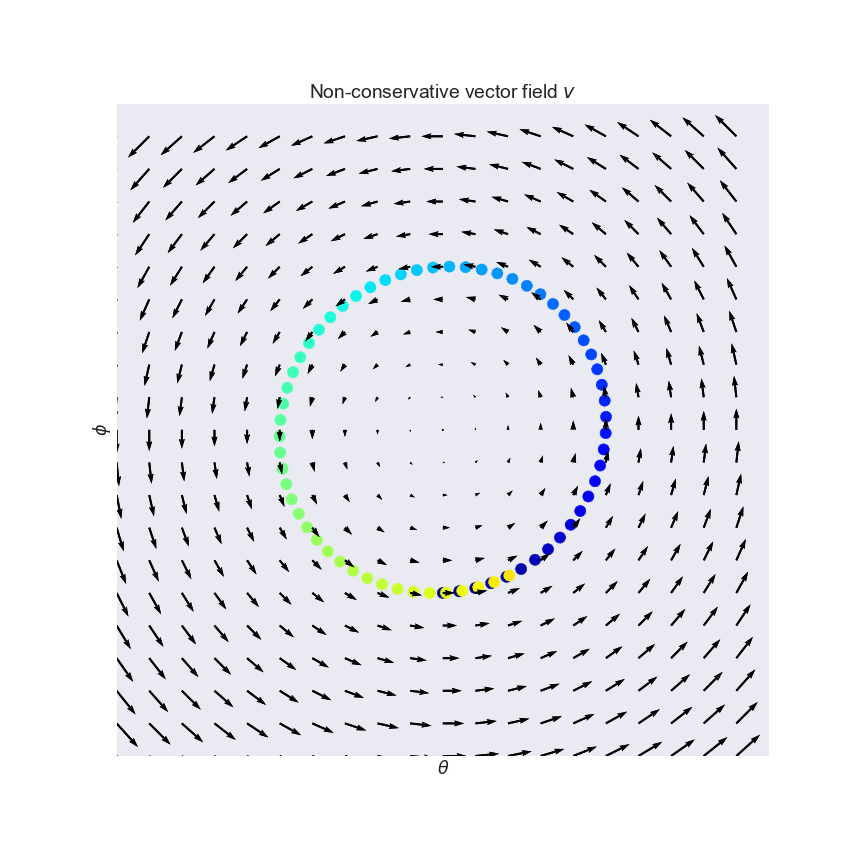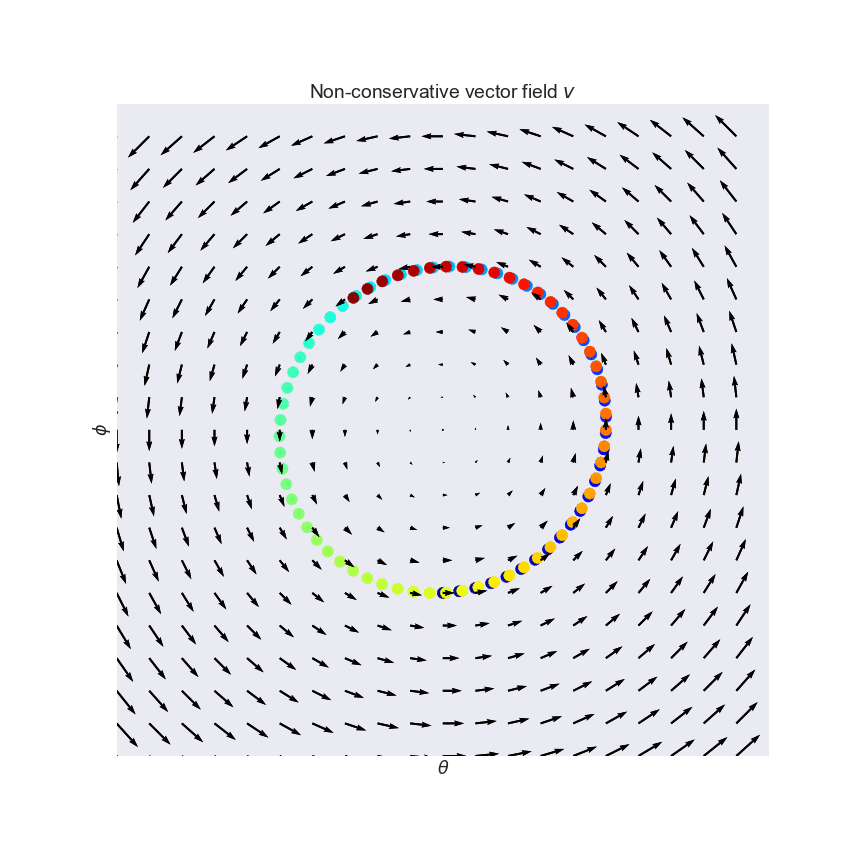
Arora, Sanjeev, Rong Ge, Yingyu Liang, Tengyu Ma, and Yi Zhang. "Generalization and equilibrium in generative adversarial nets (gans)." arXiv preprint arXiv:1703.00573 (2017)
Nagarajan, Vaishnavh, and J. Zico Kolter. "Gradient descent GAN optimization is locally stable." NIPS 2017.

GAN Summary

Jointly train two networks
Discriminator: classify data as real or fake
Generator: generate data that fools the discriminator
Many theoretical questions are still unanswered.
Many applications !! Very active area of research !!