Adversarial Games

Types of Games

• Many different kinds of games.
• Axes:
• Deterministic or stochastic?
• One, two, or more players?
• Zero sum?
• Perfect information (can you see the state)?
• Want algorithms for calculating a strategy (policy) which recommends a move from each state.

Deterministic Games

• Many possible formalizations, one is:
• States $S$ (start at $s_0$)
• Players $P=\{1, \dots, N\}$ (usually take turns)
• Actions $A$ (may depend on player / state)
• Transition Function $S \times A \rightarrow S$
• Terminal Test $S \rightarrow \{t,f\}$
• Terminal Utilities $S \times P \rightarrow R$
• Solution for a player is a policy: $S \rightarrow A$

Game Theory

• Zero-Sum Games
• Agents have opposite utilities (values on outcomes)
• Lets us think of a single value that one maximizes and the other minimizes
• Adversarial, pure competition
• General Games
• Agents have independent utilities (values on outcomes)
• Cooperation, indifference, competition, and more are all possible
• More later on non-zero-sum games

Adversarial Search

Single-Agent Trees

• Value of State: The best achievable outcome (utility) from that state
• Terminal States: $V(s)$ known
• Non-Terminal States: $V(s) = \max_{s' \in children(s)} V(s')$

Adversarial Game Trees

Minimax Values

• States Under Agent’s Control: $V(s) = \max_{s' \in successors(s)} V(s')$
• States Under Opponent's Control: $V(s') = \min_{s \in successors(s')} V(s)$
• Terminal States: $V(s)$ known

Tic-Tac Toe

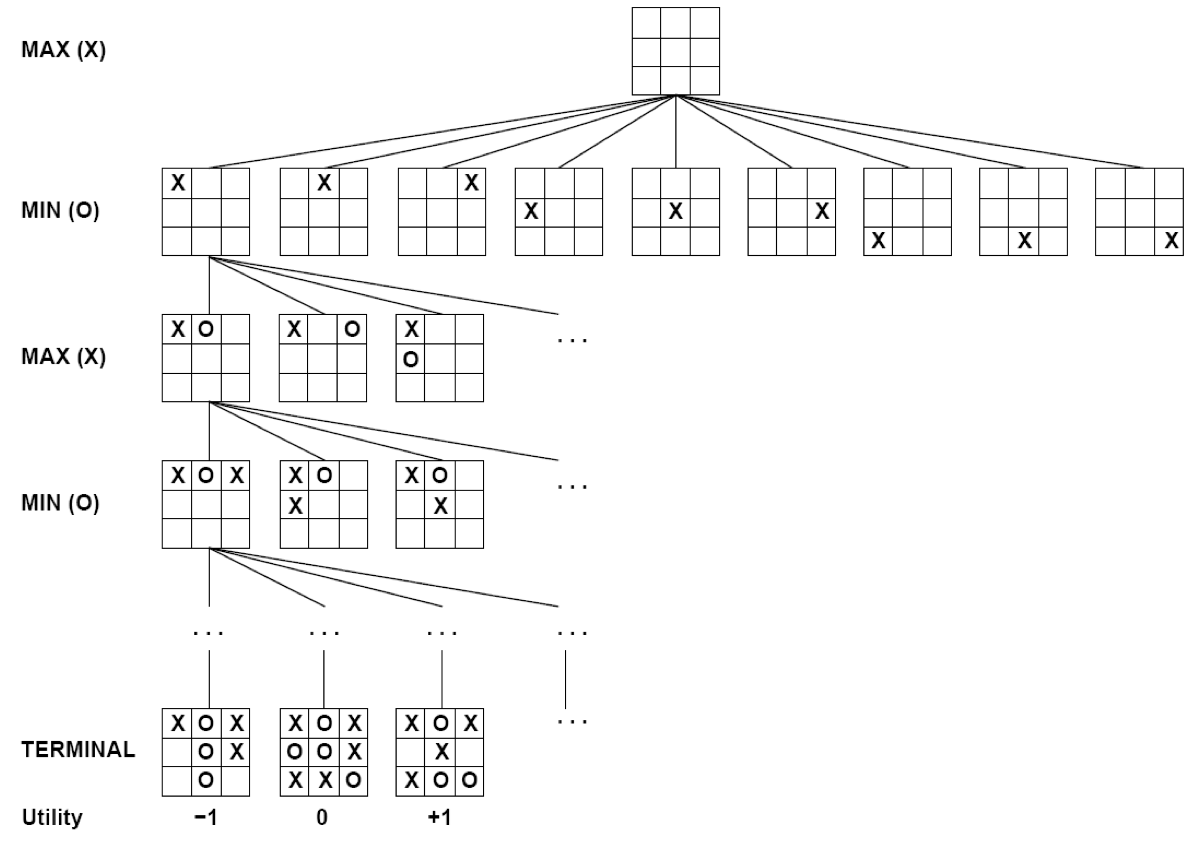
Adversarial Search (Minimax)

Minimax Implementation

Minimax Implementation (Dispatch)

Minimax Example

Minimax Properties

Minimax Efficiency

• How efficient is minimax?
• Just like (exhaustive) DFS
• Time: $\mathcal{O}(b^m)$
• Space: $\mathcal{O}(bm)$
• Example: For chess, $b \approx 35$, $m \approx 100$
• Exact solution is completely infeasible
• But, do we need to explore the whole tree?

Game Tree Pruning

Minimax Pruning

$\alpha-\beta$ Pruning

• General configuration (MIN version)
• We are computing the $MIN-VALUE$ at some node $n$
• We are looping over $n$'s children
• $n$'s estimate of the childrens’ $min$ is dropping
• Who cares about $n$'s value? $MAX$
• Let $\alpha$ be the best value that $MAX$ can get at any choice point along the current path from the root.
• If $n$ becomes worse than $\alpha$, $MAX$ will avoid it, so we can stop considering $n$'s other children (it is already bad enough that it won't be played)
• $MAX$ version is symmetric

$\alpha-\beta$ Implementation

$\alpha-\beta$ Pruning Properties

• This pruning has no effect on minimax value computed for the root.
• Values of intermediate nodes might be wrong
• Important: children of the root may have the wrong value
• So the most naïve version won’t let you do action selection
• Good child ordering improves effectiveness of pruning
• With "perfect ordering":
• Time complexity drops to $\mathcal{O}(b^{\frac{m}{2}})$
• Doubles solvable depth
• Full search of, e.g. chess, is still hopeless $\dots$
• This is a simple example of metareasoning (computing about what to compute)