Integer Programming
CSE 440: Introduction to Artificial Intelligence
Vishnu Boddeti
Content Credits: CMU AI, http://ai.berkeley.edu
Today
- Solving Linear Program
- Integer Program
- Branch and Bound
Linear Programming: What to eat?
- We are trying healthy by finding the optimal amount of food to purchase.
- We can choose the amount of stir-fry (ounce) and boba (fluid ounces).
- Health Goals
- $2000 \leq Calories \leq 2500$
- $Sugar \leq 100g$
- $Calcium \geq 700mg$
| Food | Cost | Calories | Sugar | Calcium |
|---|---|---|---|---|
| stir-fry (per oz) | 1 | 100 | 3 | 20 |
| Boba (per fl oz) | 0.5 | 50 | 4 | 70 |
- What is the cheapest way to stay "healthy" with this menu?
- How much stir-fry (ounce) and boba (fluid ounces) should we buy?
Optimization Formulation
Diet Problem $$ \begin{eqnarray} \min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\ s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b} \end{eqnarray} $$
$$A=\begin{bmatrix}-100 & -50 \\ 100 & 50 \\ 3 & 4 \\ -20 & -70\end{bmatrix} \mbox{ } b=\begin{bmatrix}-2000 \\ 2500 \\ 100 \\ -700\end{bmatrix} \mbox{ and } c=\begin{bmatrix}1 \\ 0.5\end{bmatrix}$$
Representation and Problem Solving
Problem Description
Optimization Representation $$\begin{eqnarray} \min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\ s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b} \end{eqnarray}$$
Graphical Representation
Solving an LP
- Solutions are at feasible intersections of constraint boundaries.
- Algorithms
- Check objective at all feasible intersections.
- Simplex
- Interior Point



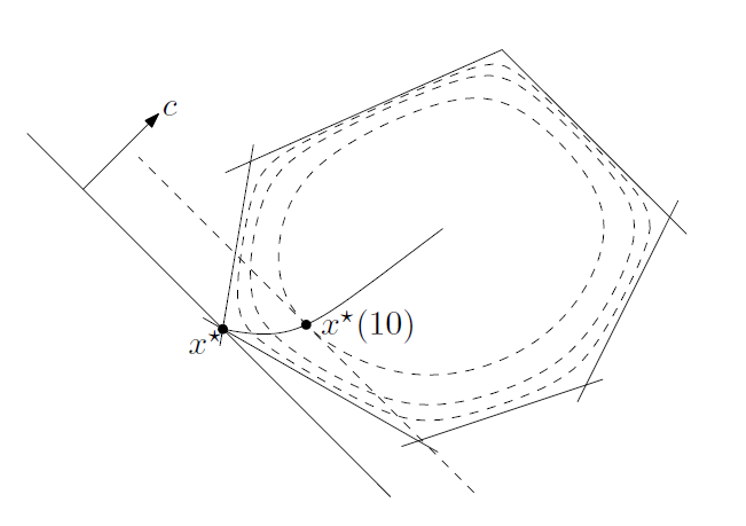
Solving an LP
But, how do we find the intersection between boundaries? $$\begin{eqnarray} \min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\ s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b} \end{eqnarray} \quad\quad A=\begin{bmatrix}-100 & -50 \\ 100 & 50 \\ 3 & 4 \\ -20 & -70\end{bmatrix} \mbox{ } b=\begin{bmatrix}-2000 \\ 2500 \\ 100 \\ -700\end{bmatrix} \mbox{ and } c=\begin{bmatrix}1 \\ 0.5\end{bmatrix}$$What about higher dimensions?
Problem Description
Optimization Representation $$\begin{eqnarray} \min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\ s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b} \end{eqnarray}$$
Graphical Representation
Shapes in higher dimensions
- How do these linear shapes extend to 3-D, N-D?
| 2-D | 3-D | N-D | |
|---|---|---|---|
| $a_1x_1+a_2x_2=b_1$ | line | plane | hyperplane |
| $a_1x_1+a_2x_2 \leq b_1$ | halfplane | halfspace | halfspace |
| $ \begin{eqnarray} a_{1,1}x_1 + a_{1,2}x_2 \leq b_1 \\ a_{2,1}x_1 + a_{2,2}x_2 \leq b_2 \\ a_{3,1}x_1 + a_{3,2}x_2 \leq b_3 \\ a_{4,1}x_1 + a_{4,2}x_2 \leq b_4 \end{eqnarray} $ | polygon | polyhedron | polytope |
Intersections in higher dimensions
- How do these linear shapes extend to 3-D, N-D?
$$
\begin{eqnarray}
\min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\
s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b}
\end{eqnarray}
$$


$$
\mathbf{A} = \begin{bmatrix} -100 & -50 & & \\ 100 & 50 & & \\ 3 & 4 & & \\ -20 & -70 & & \\ \end{bmatrix}
$$
$$
\mathbf{b} = \begin{bmatrix} -2000 \\ 2500 \\ 100 \\ -700 \end{bmatrix}
$$
Intersections in higher dimensions
- Still looking at subsets of $\mathbf{A}$ matrix
$$
\begin{eqnarray}
\min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\
s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b}
\end{eqnarray}
$$


$$
\mathbf{A} = \begin{bmatrix} -100 & -50 & & \\ 100 & 50 & & \\ 3 & 4 & & \\ -20 & -70 & & \\ \end{bmatrix}
$$
$$
\mathbf{b} = \begin{bmatrix} -2000 \\ 2500 \\ 100 \\ -700 \end{bmatrix}
$$
Linear Programming
- We are trying healthy by finding the optimal amount of food to purchase.
- We can choose the amount of stir-fry (ounce) and boba (fluid ounces).
- Health Goals
- $2000 \leq Calories \leq 2500$
- $Sugar \leq 100g$
- $Calcium \geq 700mg$
| Food | Cost | Calories | Sugar | Calcium |
|---|---|---|---|---|
| stir-fry (per oz) | 1 | 100 | 3 | 20 |
| Boba (per fl oz) | 0.5 | 50 | 4 | 70 |
- What is the cheapest way to stay "healthy" with this menu?
- How much stir-fry (ounce) and boba (fluid ounces) should we buy?
Linear $\rightarrow$ Integer
- We are trying healthy by finding the optimal amount of food to purchase.
- We can choose the amount of stir-fry (bowls) and boba (glasses).
- Health Goals
- $2000 \leq Calories \leq 2500$
- $Sugar \leq 100g$
- $Calcium \geq 700mg$
| Food | Cost | Calories | Sugar | Calcium |
|---|---|---|---|---|
| stir-fry (per bowl) | 1 | 100 | 3 | 20 |
| Boba (per glass) | 0.5 | 50 | 4 | 70 |
- What is the cheapest way to stay "healthy" with this menu?
- How much stir-fry (bowls) and boba (glasses) should we buy?
Linear vs Integer Programming
- Linear objective with linear constraints, but now with additional constraint that all values in x must be integers
$$\begin{eqnarray}
\min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\
s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b}
\end{eqnarray}$$
$$\begin{eqnarray}
\min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\
s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b} \\
&& \mathbf{x} \in \mathbb{Z}^N
\end{eqnarray}$$
- We could also do:
- Even more constrained: Binary Integer Programming
- A hybrid: Mixed Integer Linear Programming
Integer Programming: Graphical Representation
- Just add a grid of integer points onto our LP representation
Relaxation
- Relax IP to LP by dropping integer constraints
- Remember Heuristics?
Solution of Linear vs Integer Program
- Let $y^*_{IP}$ be the optimal objective of an integer program $P$.
- Let $\mathbf{x}^*_{IP}$ be the optimal point of an integer program $P$.
- Let $y^*_{LP}$ be the optimal objective of the LP-relaxed version of $P$.
- Let $\mathbf{x}^*_{LP}$ be the optimal point of the LP-relaxed version of $P$.
- Assume that $P$ is a minimization problem.
- Which of the following are true?
- $\mathbf{x}^*_{IP}=\mathbf{x}^*_{LP}$
- $y^*_{IP}\leq y^*_{LP}$
- $y^*_{IP}\geq y^*_{LP}$
$$
\begin{eqnarray}
y^*_{IP}=\min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\
s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b} \\
&& \mathbf{x} \in \mathbb{Z}^N
\end{eqnarray}
$$
$$
\begin{eqnarray}
y^*_{LP}=\min_{\mathbf{x}} && \mathbf{c}^T\mathbf{x} \\
s.t. && \mathbf{A}\mathbf{x} \preceq \mathbf{b} \\
\end{eqnarray}
$$
Solving Integer Programs: A Naive Solution
- True/False: It is sufficient to consider the integer points around the corresponding LP solution?
Solving an IP
- Branch and Bound algorithm
- Start with LP-relaxed version of IP
- If solution $\mathbf{x}^*_{LP}$ has non-integer value at $\mathbf{x}_i$
- Consider two branches with two different slightly more constrained LP problems:
- Left branch: Add constraint $\mathbf{x}_i \leq floor(\mathbf{x}^*_{LP})$
- Right branch: Add constraint $\mathbf{x}_i \geq ceil(\mathbf{x}^*_{LP})$
- Recursion. Stop going deeper:
- When the LP returns a worse objective than the best feasible IP objective you have seen before.
- When you hit an integer result from the LP
- When LP is infeasible
Branch and Bound Example


Branch and Bound Example



Q & A