Independence

Independence

• Two variables are independent if: \[\forall x,y: P(x,y) = P(x)P(y)\]
• This says that their joint distribution factors into a product of two simpler distributions
• Another form: \[\forall x,y: P(x|y)=P(x)\]
• Usually written as: $X \perp \!\!\! \perp Y$
• Independence is a simplifying modeling assumption
• Empirical joint distributions: at best "close" to independence
• What could we assume for (Weather, Traffic, Cavity, Toothache)?

Example: Independence

Example: Independence

• N fair, independent coin flips:

Conditional Independence

• P(Toothache, Cavity, Catch)
• If I have a cavity, the probability that the probe catches it does not depend on whether I have a toothache:
• $P(+catch | +toothache, +cavity) = P(+catch | +cavity)$
• The same independence holds if I do not have a cavity:
• $P(+catch | +toothache, -cavity) = P(+catch| -cavity)$
• Catch is conditionally independent of Toothache given Cavity:
• $P(catch | toothache, cavity) = P(catch | cavity)$
• Equivalent statements:
• $P(toothache | catch , cavity) = P(toothache | cavity)$
• $P(toothache, catch | cavity) = P(toothache | cavity) P(catch | cavity)$
• One can be derived from the other easily

Conditional Independence

• Unconditional (absolute) independence very rare (why?)
• Conditional independence is our most basic and robust form of knowledge about uncertain environments.
• X is conditionally independent of Y given Z i.e., $X \perp \!\!\! \perp Y | Z$
• iff: \[\forall x,y,z: \mbox{ } P(x,y|z)=P(x|z)P(y|z)\]
• or, equivalently, iff \[\forall x,y,z: \mbox{ } P(x|y,z)=P(x|z)\]

Conditional Independence

• Example 1:
• T: Traffic
• U: Umbrella
• R: Raining
• Example 2:
• F: Fire
• S: Smoke
• A: Alarm

Conditional Independence and Chain Rule

• Chain rule: $P(X_1,X_2,\dots,X_n) = P(X_1)P(X_2|X_1)P(X_3|X_2,X_1) \dots $
• Trivial decomposition: \[P(T, R, U)=P(R)P(T|R)P(U|R,T)\]
• With assumption of conditional independence: \[P(T, R, U)=P(R)P(T|R)P(U|R)\]
• Bayes nets / graphical models help us express conditional independence assumptions

Bayes Net: Big Picture

Bayes Net: Big Picture

• Two problems with using full joint distribution tables as our probabilistic models:
• Unless there are only a few variables, the joint is WAY too big to represent explicitly
• Hard to learn (estimate) anything empirically about more than a few variables at a time
• Bayes nets: a technique for describing complex joint distributions (models) using simple, local distributions (conditional probabilities)
• More properly called probabilistic graphical models
• We describe how variables locally interact
• Local interactions chain together to give global, indirect interactions

Example Bayes Net: Insurance

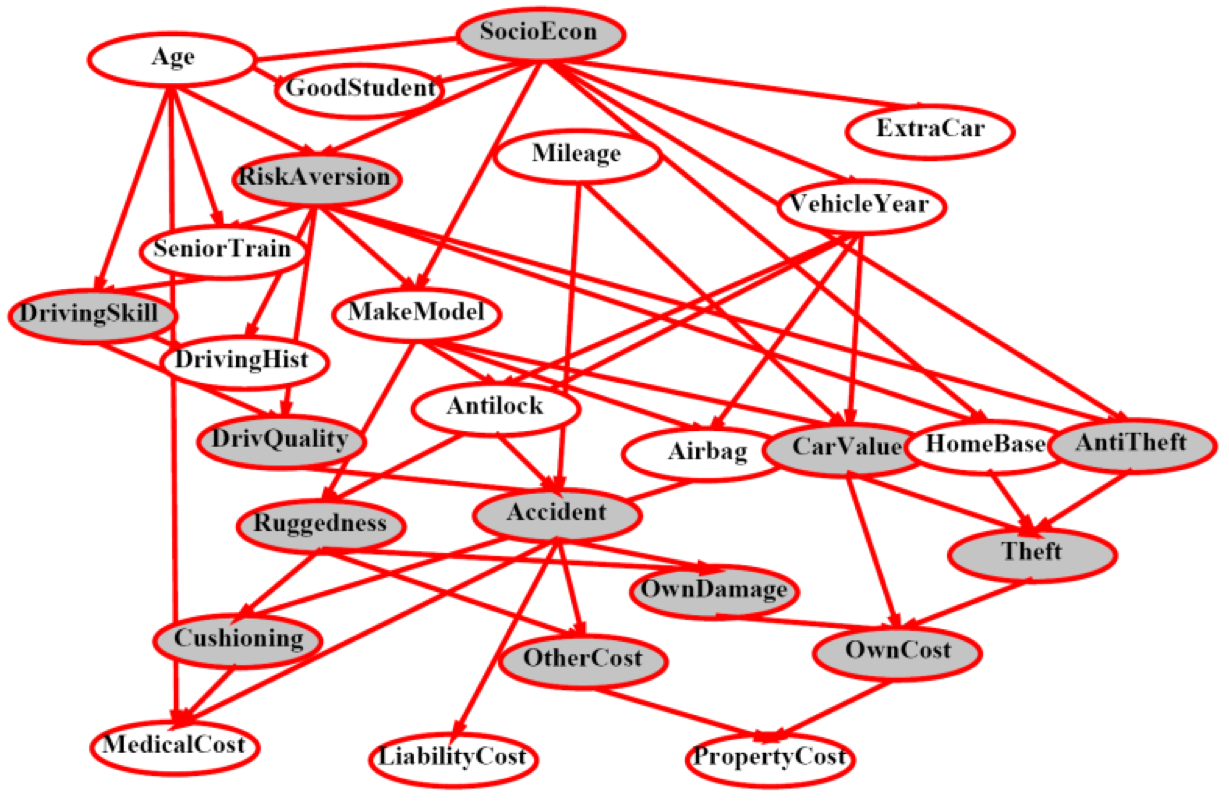
Example Bayes Net: Car

Graphical Model Notation

Example: Coin Flips

• N independent coin flips

• No interactions between variables: absolute independence

Example: Traffic

• Variables:
• R: it rains
• T: there is traffic

• Why is an agent using model 2 better?

Example: Traffic II

• How do we build a causal graphical model?


• Variables:
• T: Traffic
• R: It rains
• L: Low pressure
• D: Roof drips
• B: Ballgame
• C: Cavity

Example: Alarm Network

• How do we build a causal graphical model?


• Variables:
• B: Burglary
• A: Alarm goes off
• M: Mary calls
• J: John calls
• E: Earthquake

Bayes Net Semantics

Bayes Net Semantics

Probabilities in BNs

• Bayes nets implicitly encode joint distributions
• As a product of local conditional distributions
• To see what probability a BN gives to a full assignment, multiply all the relevant conditionals together: \[P(x_1,\dots,x_n) = \prod_{i=1}^n P(x_i|parents(x_i))\]
• Example: $P(+cavity,+catch,-toothache)$

Probabilities in BNs

• Why are we guaranteed that setting the following results in a proper joint distribution?
\[P(x_1,\dots,x_n) = \prod_{i=1}^n P(x_i|parents(x_i)) \]
• Chain rule (valid for all distributions): \[P(x_1,\dots,x_n) = \prod_{i=1}^n P(x_i|x_1,\dots,x_{i-1})\]
• Assume conditional independences: \[P(x_i|x_1,\dots,x_{i-1}) = P(x_i|parents(x_i)) \]
• Consequence: $P(x_1,\dots,x_n)=\prod_{i=1}^n P(x_i|parents(x_i))$
• Not every BN can represent every joint distribution
• The topology enforces certain conditional independencies

Example: Coin Flips

Example: Traffic

Example: Traffic

• Causal direction

Example: Reverse Traffic

• Reverse Causality?

Causality

• When Bayes nets reflect the true causal patterns:
• Often simpler (nodes have fewer parents)
• Often easier to think about
• Often easier to elicit from experts
• BNs need not actually be causal
• Sometimes no causal net exists over the domain (especially if variables are missing)
• E.g. consider the variables Traffic and Drips
• End up with arrows that reflect correlation, not causation
• What do the arrows really mean?
• Topology may happen to encode causal structure
• Topology really encodes conditional independence \[P(x_i|x_1,\dots,x_{i-1})=P(x_i|parents(x_i))\]