Applications of AI
CSE 440: Introduction to Artificial Intelligence
Vishnu Boddeti
Content Credits: CMU AI, http://ai.berkeley.edu
Applications of Techniques in CSE 440
- So Far: Foundational Methods
- Now: Applications
AlphaGo


MiniMax!!
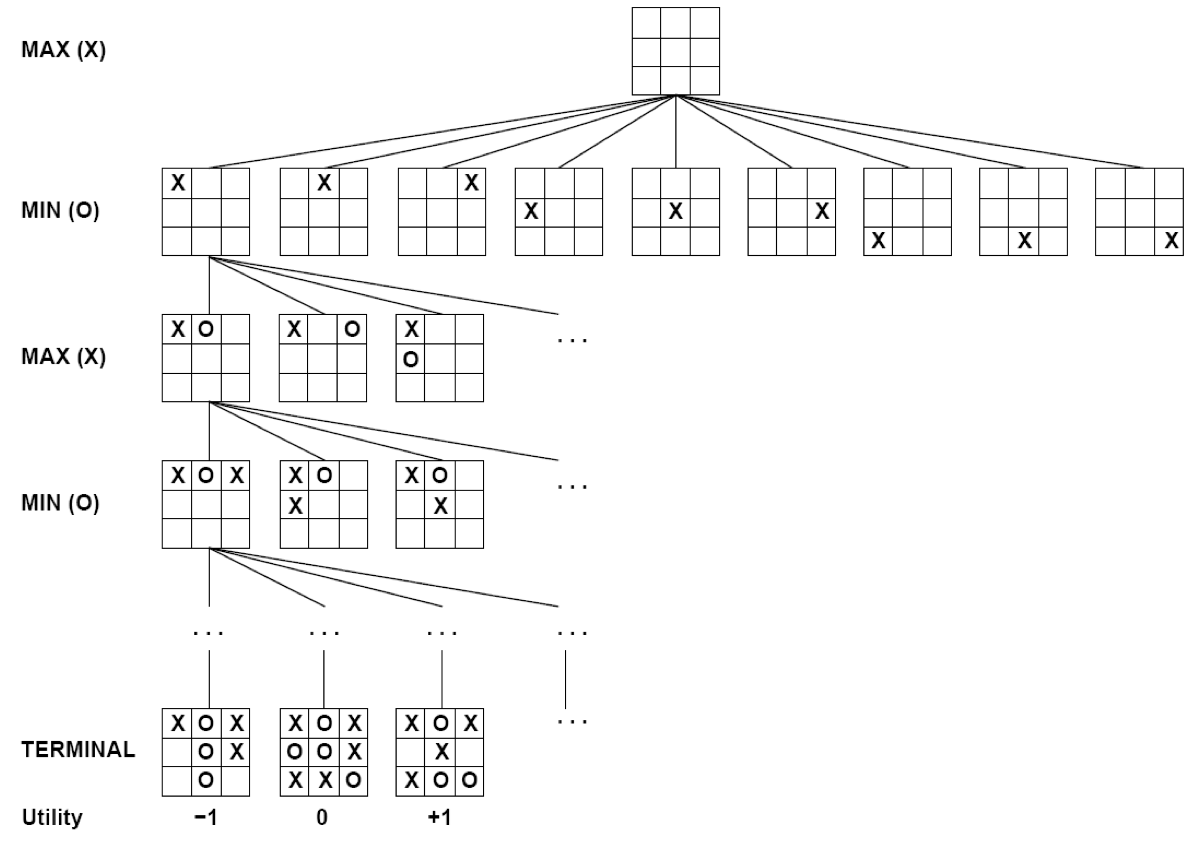
In particular, why is it harder than chess?
Exhaustive Search

Reducing Depth with Value Network

Reducing Breadth with Policy Network
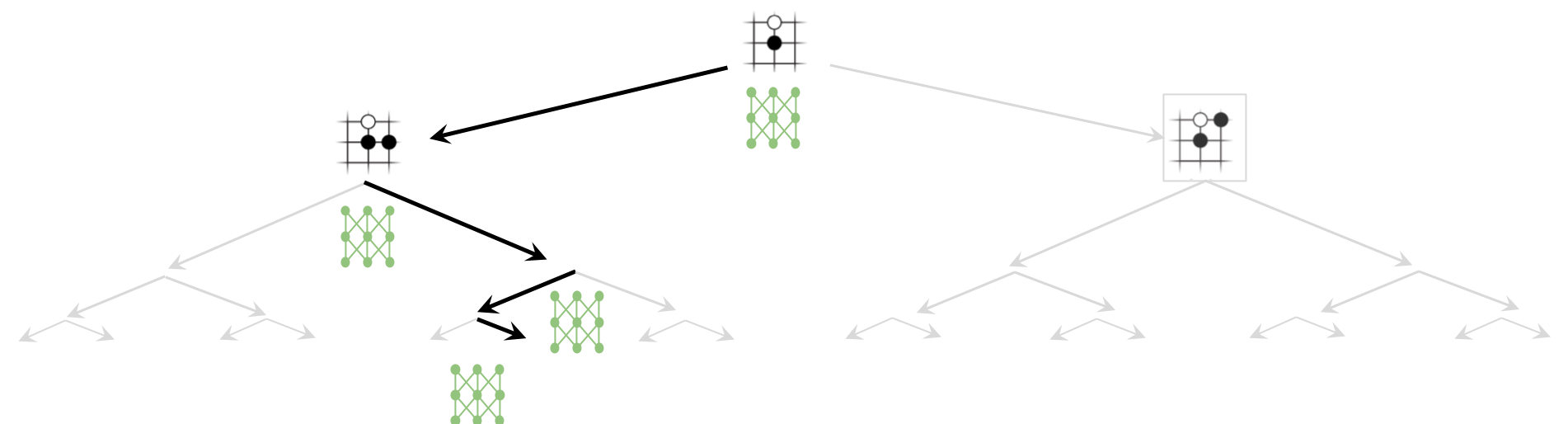
Neural Network Training Pipeline

One more thing: Monte Carlo Rollouts

Playing Games
- AlphaGo: (January 2016)
- Used imitation learning + tree search + RL
- Beat 18-time world champion Lee Sedol
- AlphaGo Zero (October 2017)
- Simplified version of AlphaGo
- No longer using imitation learning
- Beat (at the time) #1 ranked Ke Jie
- Alpha Zero (December 2018)
- Generalized to other games: Chess and Shogi
- MuZero (November 2019)
- Plans through a learned model of the game

- Silver et al, “Mastering the game of Go with deep neural networks and tree search”, Nature 2016
- Silver et al, “Mastering the game of Go without human knowledge”, Nature 2017
- Silver et al, “A general reinforcement learning algorithm that masters chess, shogi, and go through self-play”, Science 2018
- Schrittwieser et al, “Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model”, arXiv 2019
More Complex Games
- StarCraft II: AlphaStar (October 2019) Vinyals et al, "Grandmaster level in StarCraft II using multi-agent reinforcement learning", Science 2018
- Dota 2: OpenAI Five (April 2019) No paper, only a blog post: OpenAI Dota 2
Real-World Application of Deep-RL

Announcement
- Final Exam
- Next Wednesday, 16th Dec. 2020
- Syllabus: everything not included in mid-term exam i.e., MDP onwards
- Practice exam released on Piazza.
- Exam through Mimir
- Will be released at 9:55am, will close at 12:05pm.
- Students with VISA, get 30 mins extra. If you need more, contact instructor.
- Submit before Mimir closes. We will not accept late submissions. No exceptions.
- We will not accept email submissions.
- We will be available on Zoom, to answer any questions.
- Open book exam.
Robotic Helicopters
Motivating Example
- How do we execute a task like this?
Autonomous Helicopter Flight


- Key challenges:
- Track helicopter position and orientation during flight
- Decide on control inputs to send to helicopter
Autonomous Helicopter Setup

HMM for Tracking the Helicopter

- State: $s=(x,y,z,\phi,\theta,\psi,\dot{x},\dot{y},\dot{z},\dot{\phi},\dot{\theta},\dot{\psi})$
- Measurements:
- 3-D coordinates from vision, 3-axis magnetometer, 3-axis gyro, 3-axis accelerometer
- Transition dynamics:
- $s_{t+1}=f(s_t,a_t) + w_t$
- $f$ encodes helicopter dynamics
- $w$ is a probabilistic noise model
Helicopter MDP
- State: $s=(x,y,z,\phi,\theta,\psi,\dot{x},\dot{y},\dot{z},\dot{\phi},\dot{\theta},\dot{\psi})$
- Actions (control inputs):
- $a_{lon}$: Main rotor longitudinal cyclic pitch control (affects pitch rate)
- $a_{lat}$: Main rotor latitudinal cyclic pitch control (affects roll rate)
- $a_{coll}$: Main rotor collective pitch (affects main rotor thrust)
- $a_{rud}$: Tail rotor collective pitch (affects tail rotor thrust)
- Transitions (dynamics):
- $s_{t+1}=f(s_t,a_t) + w_t$
- $f$ encodes helicopter dynamics
- $w$ is a probabilistic noise model
- What else do we need to solve the MDP?
Problem: What is the reward?
- Reward for hovering: \begin{equation} \begin{aligned} R(s) &= -\alpha_x(x-x^{*})^2 \nonumber \\ &= -\alpha_y(y-y^{*})^2 \nonumber \\ &= -\alpha_z(z-z^{*})^2 \nonumber \\ &= -\alpha_{\dot{x}}\dot{x}^2 \nonumber \\ &= -\alpha_{\dot{y}}\dot{y}^2 \nonumber \\ &= -\alpha_{\dot{z}}\dot{z}^2 \nonumber \end{aligned} \end{equation}
RL: Helicopter Flight
Problems for More General Case: What is the Reward?
- Rewards for "Flip"?
- Problem: what’s the target trajectory?
- Just write it down by hand?
Flips?
Helicopter Apprenticeship from Demonstrations
Learning a Trajectory

- HMM-like generative model
- Dynamics model used as HMM transition model
- Demos are observations of hidden trajectory
- Problem: how do we align observations to hidden trajectory?
Probabilistic Alignment using Bayes' Net

- Dynamic Time Warping
- (Needleman and Wunsch 1970, Sakoe and Chiba, 1978)
- Extended Kalman filter / smoother
Aligned Demonstrations
Alignment of Samples
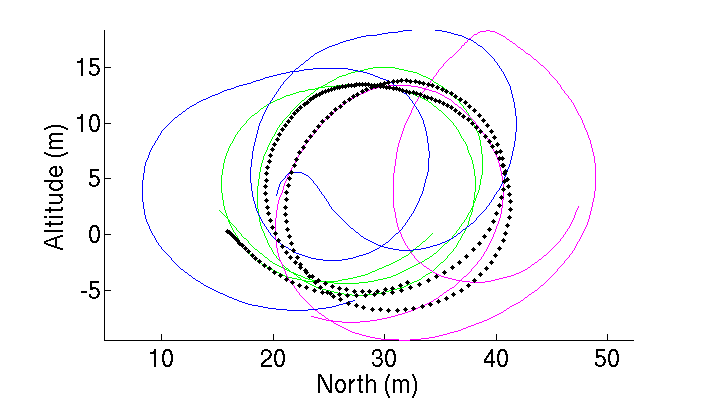
- Result: inferred sequence is much cleaner.
Learned Behavior
Legged Locomotion
DARPA Robotics Challenge (2015)
How about continuous control, i.e., locomotion?
- Robot models in physics simulator (MuJoCo, from Emo Todorov)
- Input:
- joint angles and velocities
- Output:
- joint torques

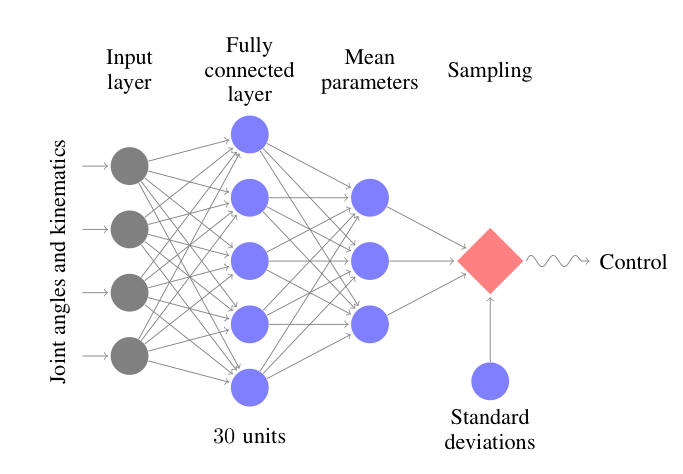
Learning Locomotion
Deep RL: Virtual Stuntman
Quadruped

- Low-level control problem: moving a foot into a new location
- search with successor function $\sim$ moving the motors
- High-level control problem: where should we place the feet?
- Reward function $R(x) = w . f(s)$ (25 features)
Reward Learning + Reinforcement Learning
- Demonstrate path across the "training terrain"
- Learn the reward function
- Receive "testing terrain" - height map.
- Find the optimal policy with respect to the {\color{green!60!black} learned reward function} for crossing the testing terrain.


Without Reward Learning
With Reward Learning
Autonomous Driving
DARPA Challenge 2005: Barstow, CA to Primm, NV
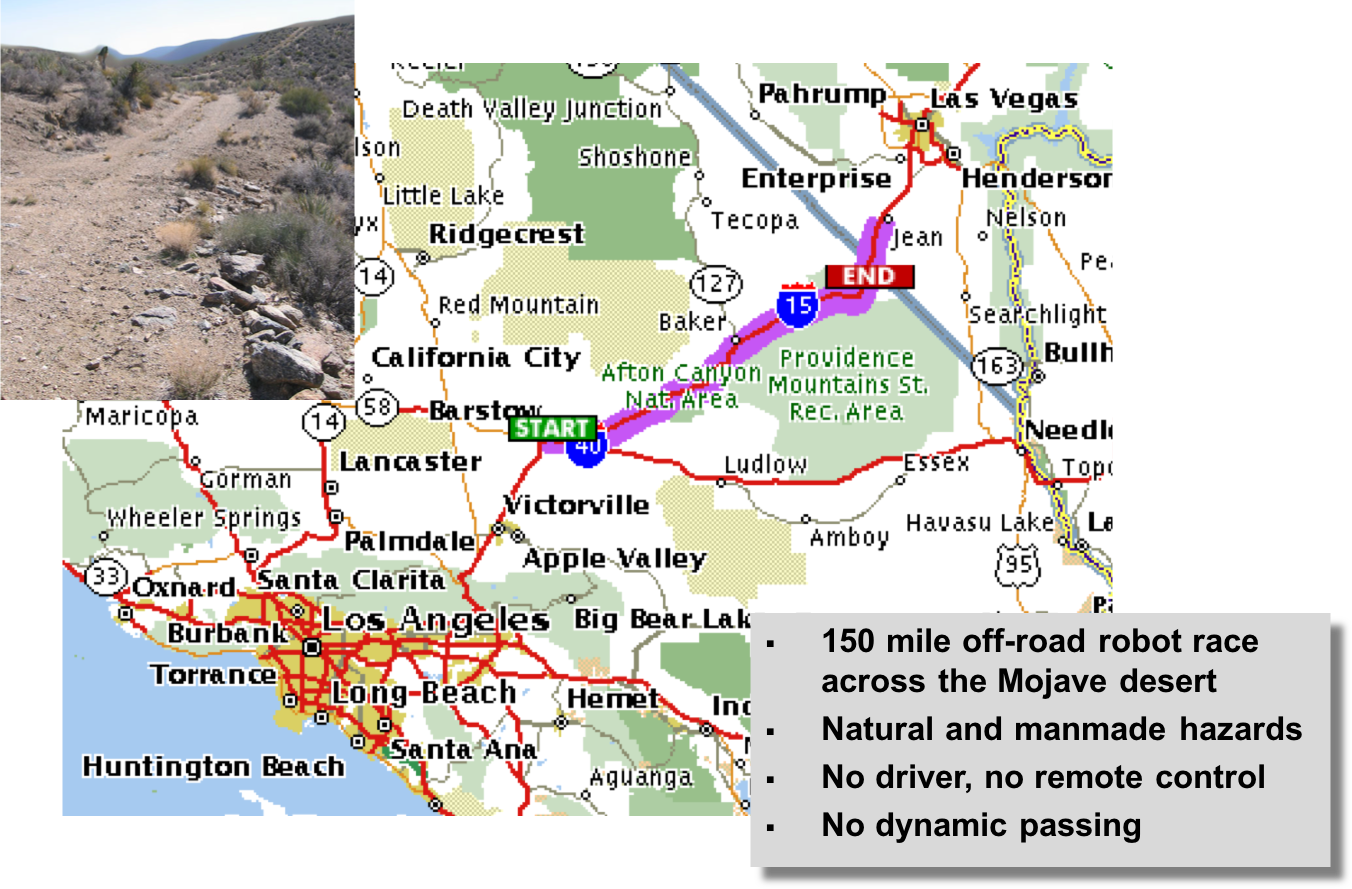
Autonomous Vehicles

Grand Challenge 2005 Nova Video
Grand Challenge 2005 - Bad
Autonomous Cars
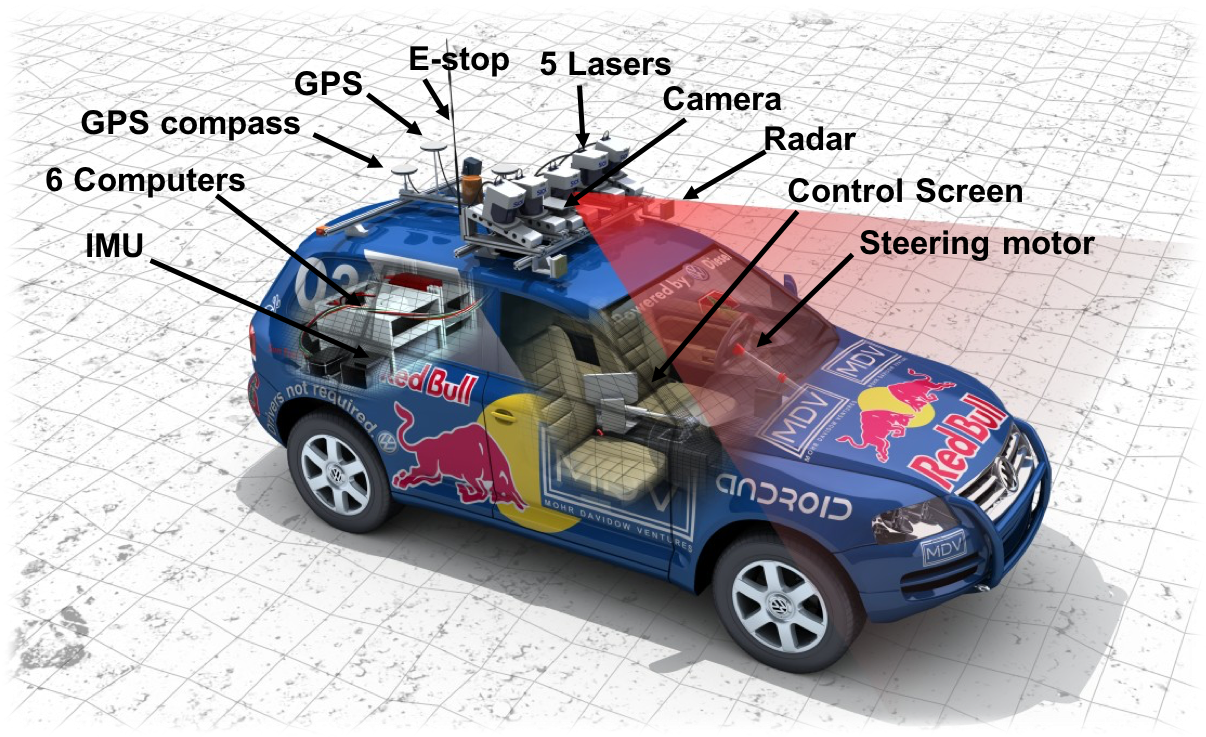
Actions: Steering Control
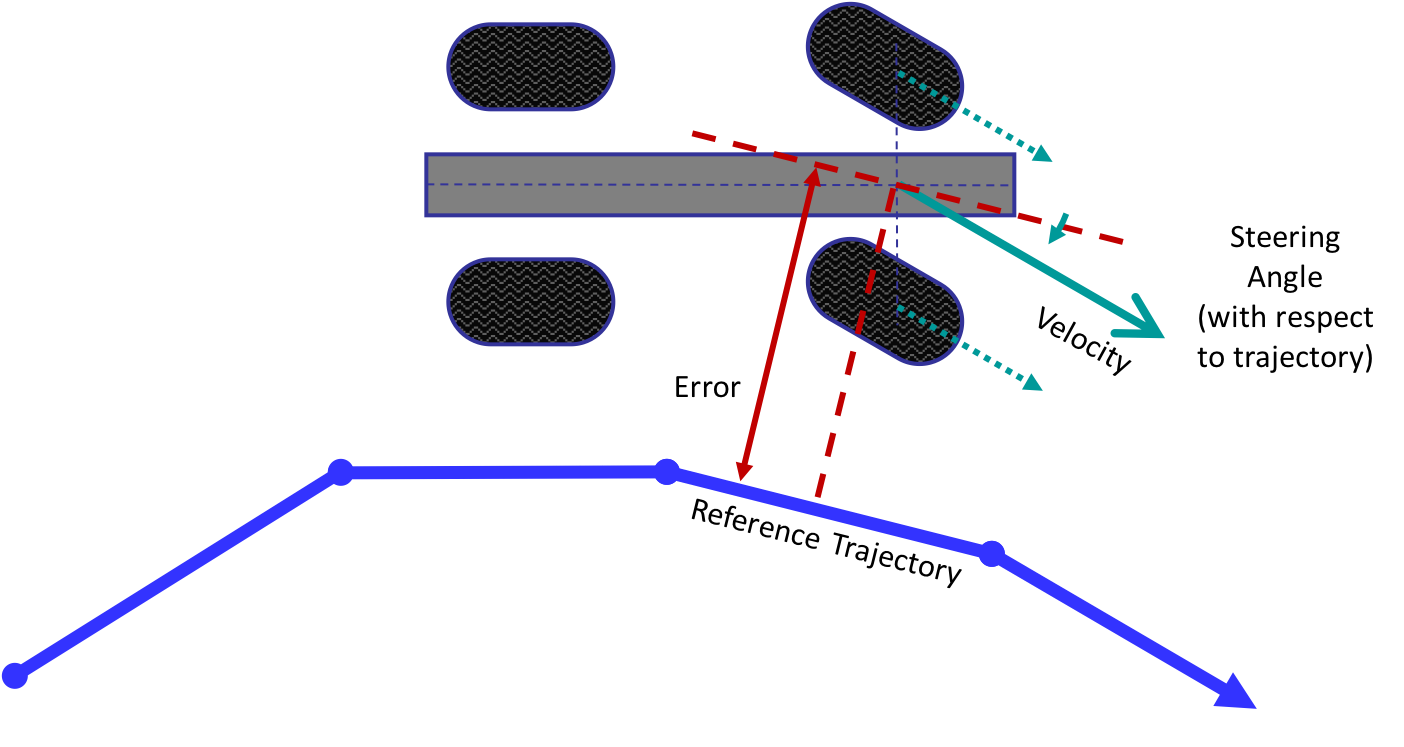
Obstacle Detection
- Trigger if $|Z_i-Z)j|>15cm$ for nearby $z_i$ and $z_j$
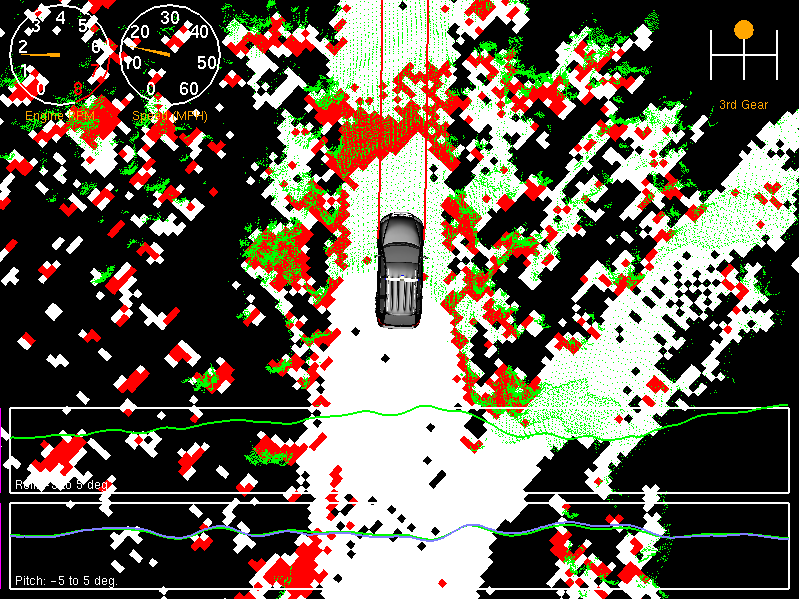
Probabilistic Error Model

HMMs for Detection


Sensors: Cameras


Vision for a Car
Self-Supervised Vision
Google Self-Driving Car (2013)
Recent Progress: Semantic Segmentation

Self-Driving Cars: Stats
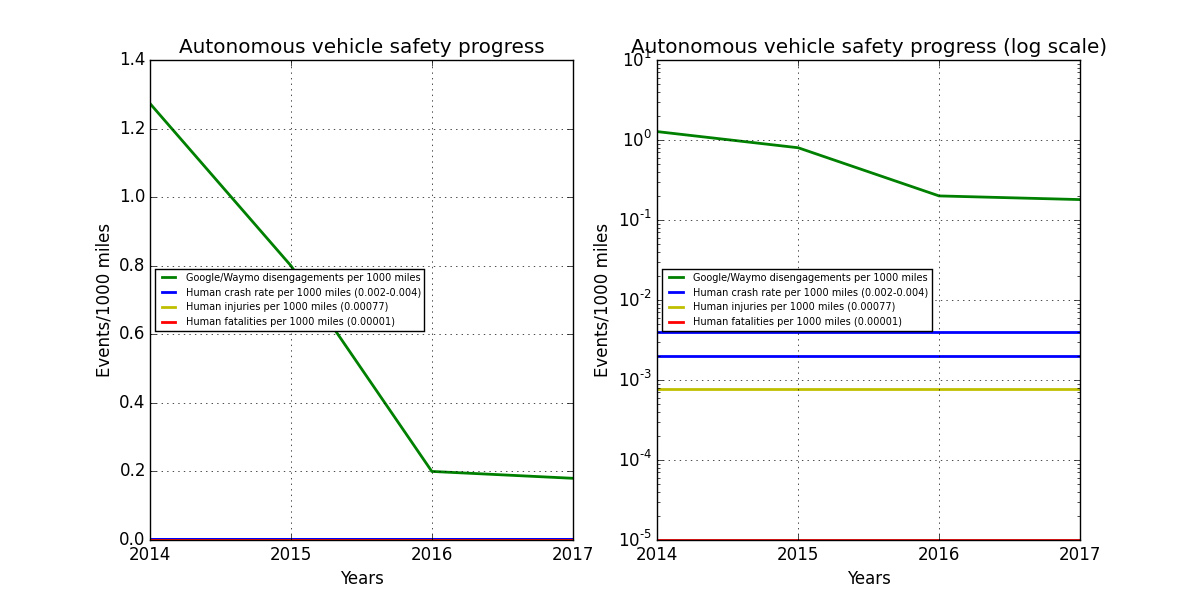
Self-Driving Cars: Stats

Personal Robotics
PR-1
Challenge Task: Robotic Laundry
Sock Sorting
How about a range of skills?
Reinforcement Learning
Learned Skills
Q & A