Feed Forward Networks: Introduction

Feed Forward Networks: Introduction

CSE 891: Deep Learning

Vishnu Boddeti

Today

Artificial Neuron
Activation Functions
Capacity of Neural Networks
Biological Motivation

XKCD

Simplest Neural Network

Artificial Neuron

Neuron pre-activation (or input activation)
$a(\mathbf{x}) = b + \sum_i w_ix_i = b + \mathbf{w}^T\mathbf{x}$
Neuron (output) activation
$h(\mathbf{x}) = g(a(\mathbf{x})) = g\left(b+\sum_iw_ix_i\right)$
$\mathbf{w}$ are the connection weights
$b$ is the neuron bias
$g(\cdot)$ is called activation function

Artificial Neuron

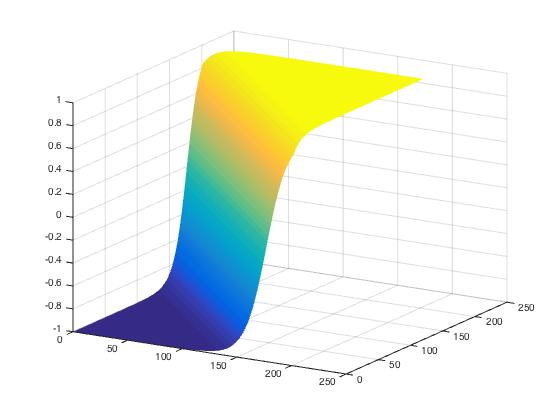
range determined by $g(\cdot)$
bias $b$ only changes the position of the riff

Linear Activation

$g(x)=x$

Performs no input squashing
Quite a boring function...

Sigmoid Activation

$g(x)=\frac{1}{1+e^{-x}}$

Squashes the neuron's pre-activation between 0 and 1
Always positive
Bounded
Strictly increasing

Tanh Activation

$g(x)=\frac{e^{x}-e^{-x}}{e^{x}+e^{-x}}$

Squashes the neuron's pre-activation between -1 and 1
Can be positive or negative
Bounded
Strictly increasing

Rectified Linear Unit Activation

$g(x)=max(0,x)$

Bounded below by 0 (always non-negative)
Not upper bounded
Strictly increasing
Tends to yeild neurons with sparse activities

Capcity of Neural Networks

Single Neuron

Could do binary classification:

with sigmoid, can interpret neuron as estimating $p(y=1|\mathbf{x})$
also known as logistic regression classifier
if greater than 0.5, predict class 1
otherwise, predict class 0
similar idea can be used with Tanh

decision boundary is linear

Capacity of a Single Neuron

Can solve linearly seperable problems

Capacity of a Single Neuron

Cannot solve non-linearly separable problems....

...unless the input is transformed in a better representation

Neural Network with Hidden Layer

Hidden layer pre-activation:

$\mathbf{a}(\mathbf{x}) = \mathbf{b}_1 + \mathbf{W}_1\mathbf{x}$

$\left(a(\mathbf{x})^i = \mathbf{b}^i_1 + \sum_{j}W^{i,j}_1x^j\right)$

Hidden layer activation:

$\mathbf{h}(\mathbf{x}) = \mathbf{g}(\mathbf{a}(\mathbf{x}))$

Output layer activation:

$f(\mathbf{x}) = o(b_2 + \mathbf{w}_2^T\mathbf{h}(\mathbf{x}))$

Softmax Activation Function

For multi-class classification:

we need multiple outputs (1 output per class)
we would like to estimate the conditional probability $p(y=c|\mathbf{x})$

Softmax activation function at the output:

$\mathbf{o}(\mathbf{a}) = \textrm{softmax}(\mathbf{a}) = \left[\frac{\exp{a_1}}{\sum_c\exp{a_c}},\dots,\frac{\exp{a_C}}{\sum_c\exp{a_c}}\right]^T$

strictly positive
sums to one

Predicted class: one with highest estimated probability

Multi-Layer Neural Network

Could have $L$ hidden layers:

layer pre-activation for $k>0$ ( $\mathbf{h}^{(0)}(\mathbf{x})=\mathbf{x}$ )

$\mathbf{a}^{(k)}(\mathbf{x}) = \mathbf{b}^{(k)} + \mathbf{W}^{(k)}\mathbf{h}^{(k-1)}(\mathbf{x})$

hidden layer activation ( $k$ from 1 to $L$ ):

$\mathbf{h}^{(k)}(\mathbf{x}) = \mathbf{g}(\mathbf{a}^{(k)}(\mathbf{x}))$

output layer activation ( $k=L+1$ ):

$\mathbf{h}^{(L+1)}(\mathbf{x}) = \mathbf{o}(\mathbf{a}^{(L+1)}(\mathbf{x})) = f(\mathbf{x})$

Capacity of Single Hidden Layer Neural Network

Universal Approximation

Universal approximation theorem (Hornik, 1991):

"a single hidden layer neural network with a linear output unit can approximate any continuous function arbitrarily well, given enough hidden units"

The result applies for sigmoid, tanh and many other hidden layer activation functions.
This is a good result, but it doesn’t mean there is a learning algorithm that can find the necessary parameter values.
Many other function classes also known to be universal approximators.

Biological Inspiration

Biological and Artificial Neurons

Yamins and Dicarlo 2016

Yamins and DiCarlo, 2016

Biological and Artificial Neurons

Yamins and Dicarlo 2016

Yamins and DiCarlo, 2016

Transistors and Biological Neurons

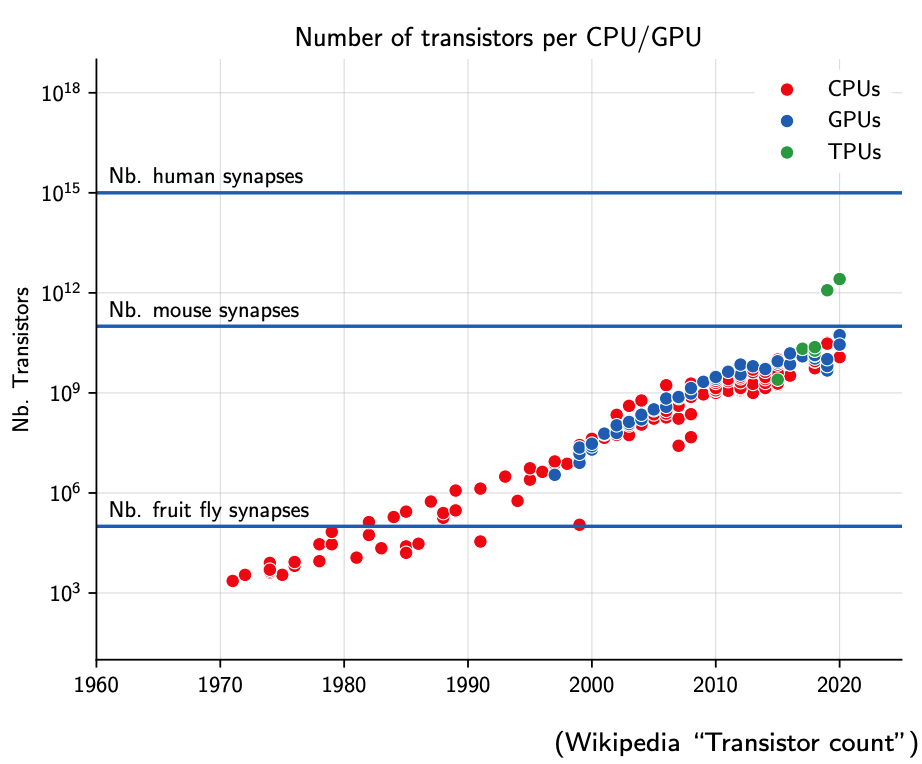
transistor count

Image Credit: Francois Fleuret

Q & A

XKCD

Feed Forward Networks: Introduction CSE 891: Deep Learning Vishnu Boddeti