Optimization
CSE 891: Deep Learning
Vishnu Boddeti
Overview
- So far we saw how to compute gradients, and how to compute them efficiently. What do we actually do with the gradients?
- Today's lecture: gradient descent, various things that can go wrong in gradient descent, and what to do about them.
- Assume that all the parameters we wish to learn have been grouped into a single vector $\mathbf{\theta}$.
What is Optimization?
$$\mathbf{w}^* = \mbox{arg} \min_{\mathbf{w}} \mathcal{L}(\mathbf{w})$$Optimization

Gradient Descent
- Gradient Descent: procedure to minimize a function
- Optimizes a linear approximation of the function at the given point. \[f(\mathbf{x}) = f(\mathbf{x}_0) + (\mathbf{x}-\mathbf{x}_0)^T\nabla_{\mathbf{x}}f(\mathbf{x}_0)\]
- compute gradient \[f'(\mathbf{x}_0) = \nabla_{\mathbf{x}}f(\mathbf{x}_0)\]
- take step in opposite direction \[\Delta \mathbf{x}_0 = -\nabla_{\mathbf{x}}f(\mathbf{x}_0)\]
Gradient Descent...
- Iteratively step in the direction of the negative gradient (direction of local steepest descent)
# vanilla gradient descent
w = initialize_weights()
for t in range(num_steps):
dw = compute_gradients(loss_fn, data, w)
w -= learning_rate * dw
- hyperparameters
- weight initialization method
- number of steps
- learning rate



Gradient Descent
- Gradient descent for empirical risk minimization
- initialize $\mathbf{\theta}$
- for T iterations $$ \begin{eqnarray} \nabla_{\mathbf{\theta}}J(\mathbf{\theta}) &=& \frac{1}{N}\sum_n\nabla_{\theta}l(f(\mathbf{x}_n;\mathbf{\theta}),\mathbf{y}_n)+\lambda\nabla_{\mathbf{\theta}}\Omega(\mathbf{\theta}) \nonumber \\ \mathbf{\theta}_{t+1} &=& \mathbf{\theta}_{t} - \alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta}_t) \nonumber \end{eqnarray} $$
Variants of Gradient Descent
- Batch Gradient Descent: \[\Delta_{\mathbf{\theta}} = \frac{1}{N}\sum_n\nabla_{\theta}l(f(\mathbf{x}_n;\mathbf{\theta}),\mathbf{y}_n)\]
- Stochastic Gradient Descent: \[\Delta_{\mathbf{\theta}} = \nabla_{\theta}l(f(\mathbf{x}_n;\mathbf{\theta}),\mathbf{y}_n)\]
- Mini-Batch Gradient Descent: \[\Delta_{\mathbf{\theta}} = \frac{1}{m}\sum_{n \in M}\nabla_{\theta}l(f(\mathbf{x}_n;\mathbf{\theta}),\mathbf{y}_n)\]
Stochastic Gradient Descent
- Algorithm that performs updates after each example.
- initialize $\mathbf{\theta}$
- for N iterations:
- for each training example $(\mathbf{x}_n,\mathbf{y}_n)$ $$\begin{eqnarray} J(\mathbf{\theta}) &=& \frac{1}{m}\sum_{n \in M} l(f(\mathbf{x}_n,\mathbf{\theta}),\mathbf{y}_n) + \lambda\Omega(\mathbf{\theta}) \nonumber \\ \mathbf{\theta}_t &=& \mathbf{\theta}_{t-1} - \alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta}_{t-1}) \nonumber \end{eqnarray}$$
- Hyperparameters
- $\alpha$ is the learning rate, typically follows an annealing schedule.
- batch size, 32/64/128 common
- data sampling, has to be randomized
SGD With Noise
- Another variant: use noisy gradients
- Anneal the noise down with iterations
Optimization Landscapes
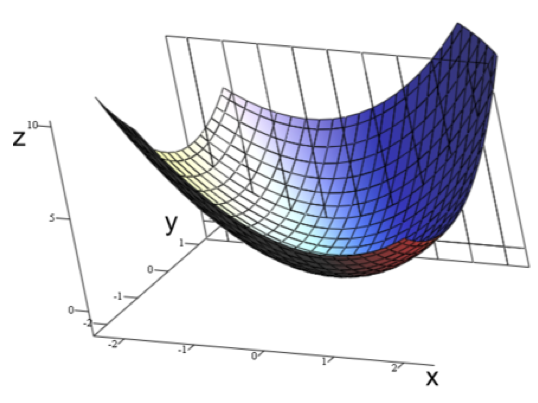


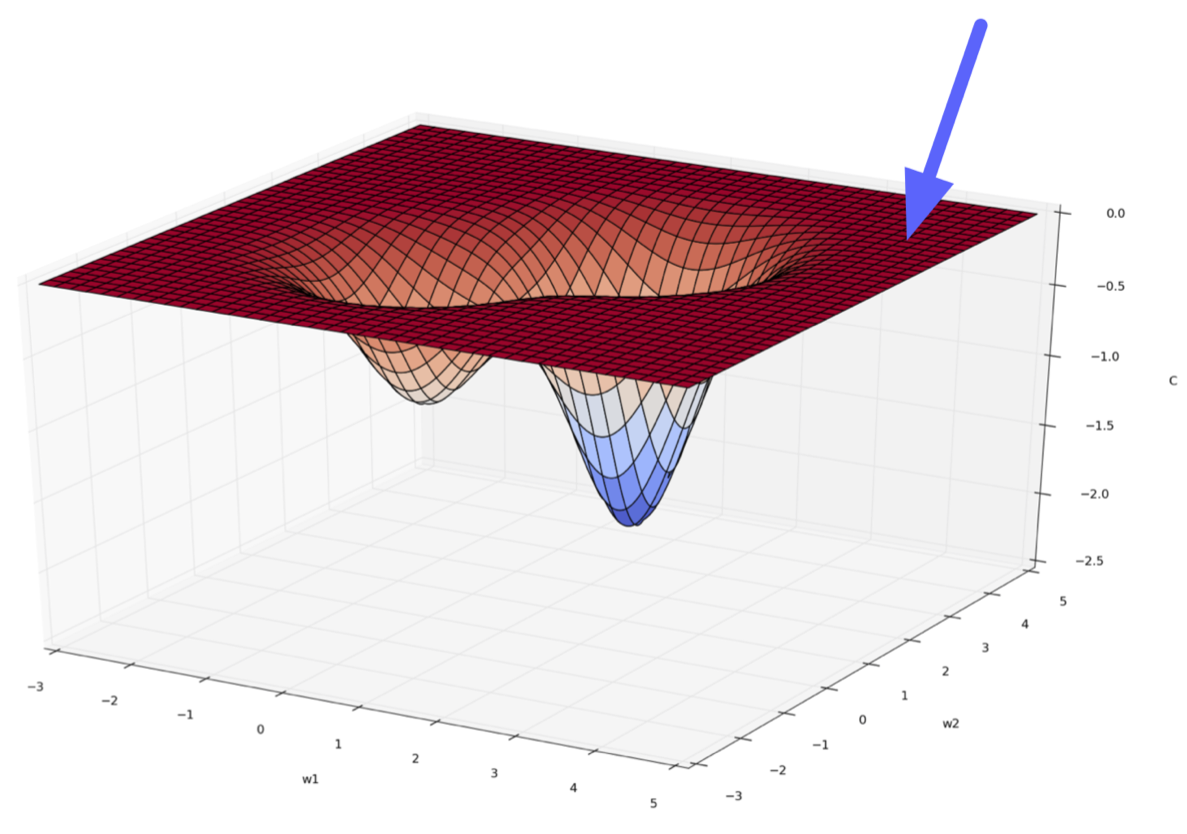
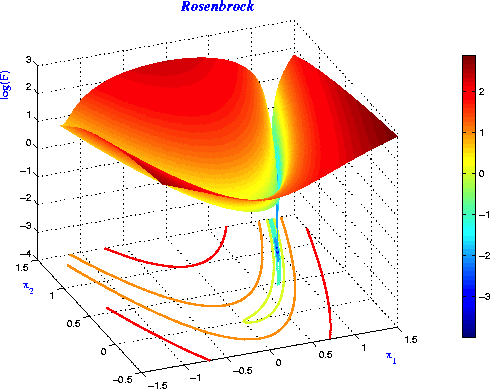
Local Minima
- If a function is convex, it has no spurious local minima, i.e. any local minimum is also a global minimum.
- So SGD is guaranteed to eventually reach the global minimum.
- Unfortunately, training a network with hidden units cannot be convex because of permutation symmetries.
- we can re-order the hidden units in a way that preserves the function computed by the network.

Local Minima (Fear Not)
- Generally, local minima are not something we worry much about when we train most neural nets.
- They are normally only a problem if there are local minima "in function space". E.g., CycleGANs have a bad local minimum where they learn the wrong color mapping between domains.
- It is possible to construct arbitrarily bad local minima even for ordinary classification MLPs. We not fully understand why they don't arise in practice.
- Intuitively, if you have enough randomly sampled hidden units, you can approximate any function just by adjusting the output layer.
- It reduces to a regression problem, which is convex.
- Hence, local optima can probably be fixed by adding more hidden units.
- We do not have a rigorous proof, but we have ample empirical evidence.
- Over the past 5 years or so, CS theorists have made lots of progress proving gradient descent converges to global minima for some non-convex problems, including some specific neural net architectures.
Saddle Points

- A saddle point is a point where:
- $\nabla \mathcal{L}(\mathbf{\theta})=\mathbf{0}$
- The Hessian $\mathbf{H}(\mathbf{\theta})$ has some positive and some negative eigenvalues, i.e., some directions with positive curvature and some with negative curvature
Saddle Points: A Problem?
- When would saddle points be a problem?
- Suppose you have two hidden units with identical incoming and outgoing weights.
- After a gradient descent update, they will still have identical weights. By induction, they’ll always remain identical.
- But if you perturbed them slightly, they can start to move apart.
- Important special case: never initialize all your weights to zero!
- Instead, break the symmetry by using small random values.
Plateaux
- A flat region is called a plateau. (Plural: plateaux)
- Can you think of examples?
- 0-1 loss
- hard threshold activations
- logistic activations and least-squares

Plateaux
- An important example of a plateau is a saturated unit. This is when it is in the flat region of its activation function. Recall the backprop equation for the weight derivative:
$$\begin{equation}
\begin{aligned}
z_i' &= h'\phi'(z) \\
w_{ij}' &= z_i'x_j
\end{aligned}
\end{equation}$$

- If $\phi'(z_i)$ is always close to zero, then the weights will get stuck.
- If there is a ReLU unit whose input $z_i$ is always negative, the weight derivatives will be exactly $0$. We call this a dead unit.
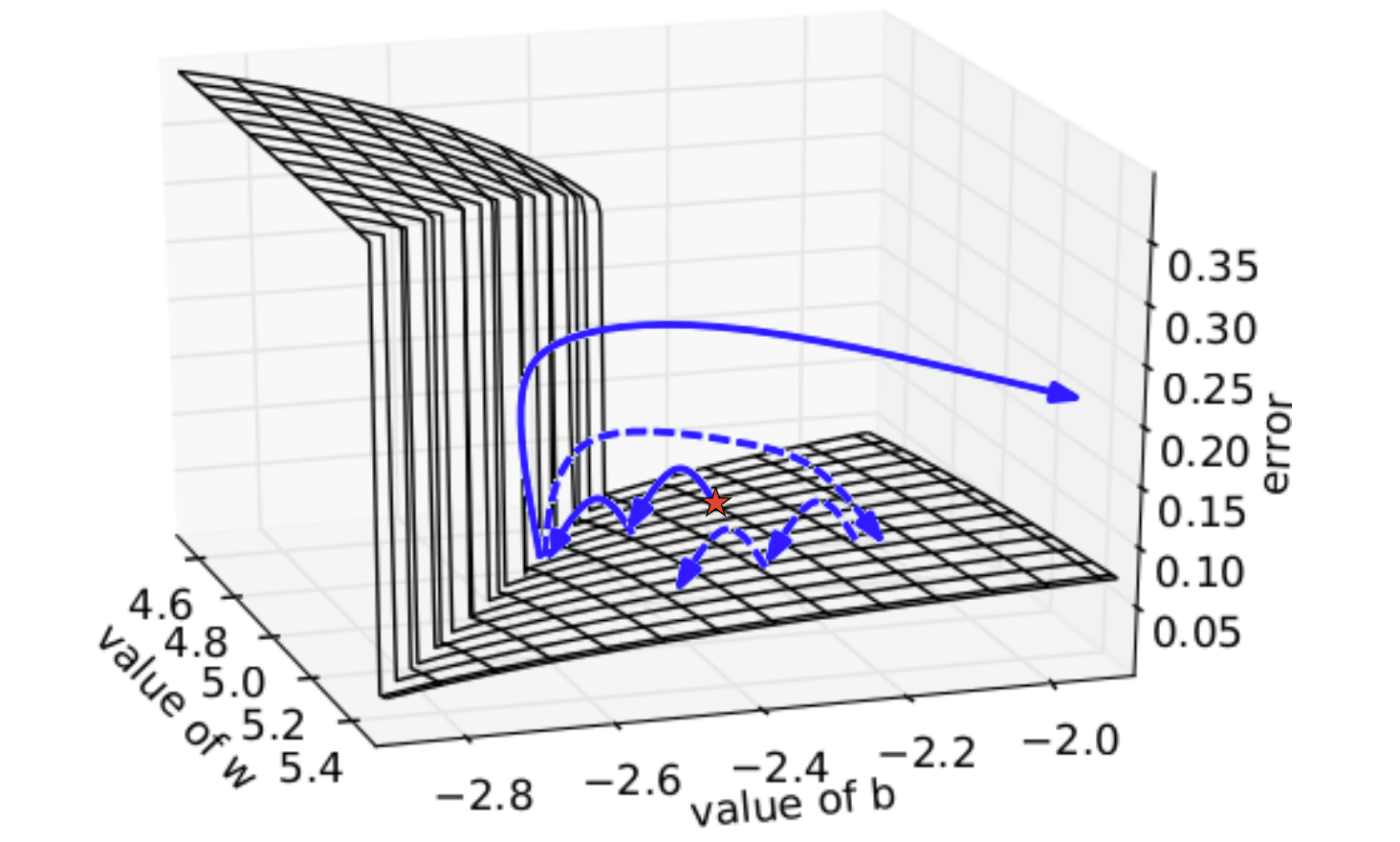
Ill-Conditioned Curvature


- Suppose Hessian $\mathbf{H}$ has some large positive eigenvalues (i.e. high-curvature directions) and some eigenvalues close to 0 (i.e. low-curvature directions).
- Gradient descent bounces back and forth in high curvature directions and makes slow progress in low curvature directions.
- To interpret this visually: the gradient is perpendicular to the contours.
- This is known as ill-conditioned curvature. It’s very common in neural net training.
Gradient Descent...

Ill-Conditioned Curvature
| $x_1$ | $x_2$ | $t$ |
|---|---|---|
| 100.8 | 0.00345 | 5.1 |
| 340.1 | 0.00181 | 3.2 |
| 200.2 | 0.00267 | 4.1 |
| $\vdots$ | $\vdots$ | $\vdots$ |
- Suppose we have the following dataset for linear regression.
- Which weight, $w_1$ or $w_2$, will receive a larger gradient descent update?
- Which one do you want to receive a larger update?
Ill-Conditioned Curvature
- Another Example:
| $x_1$ | $x_2$ | $t$ |
|---|---|---|
| 1003.2 | 1005.1 | 3.3 |
| 1001.1 | 1008.2 | 4.8 |
| 998.3 | 1003.4 | 2.9 |
| $\vdots$ | $\vdots$ | $\vdots$ |
Curvature Normalization
- To avoid these problems, it is a good idea to center your inputs to zero mean and unit variance, especially when they are in arbitrary units (feet, seconds, etc.). $$\tilde{x}_j = \frac{x_j-u_j}{\sigma_j}$$
- Hidden units may have non-centered activations, and this is harder to deal with.
- One trick: replace logistic units (which range from 0 to 1) with Tanh units (which range from -1 to 1)
- A normalization method called batch normalization explicitly centers each hidden activation. It often speeds up training by 1.5-2x, and it is available in all the major neural net frameworks.
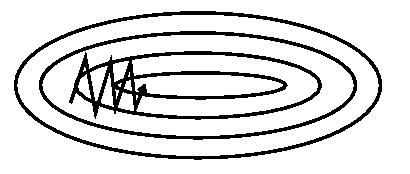
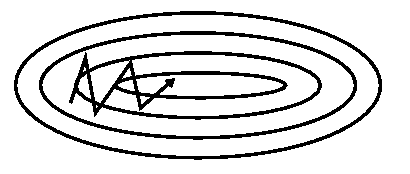
Momentum
- Unfortunately, even with these normalization tricks, ill-conditioned curvature is a fact of life. We need algorithms that are able to deal with it.
- Momentum:
- Nesterov Accelerated Gradient:
$$\begin{eqnarray}
\mathbf{v}_t &=& \gamma\mathbf{v}_{t-1} + \alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta}) \nonumber \\
\mathbf{\theta}_t &=& \mathbf{\theta}_{t-1} - \mathbf{v}_t \nonumber
\end{eqnarray}$$
$$\begin{eqnarray}
\mathbf{v}_t &=& \gamma\mathbf{v}_{t-1} + \alpha\nabla_{\mathbf{\theta}}J(\mathbf{\theta-\gamma\mathbf{v}_{t-1}}) \nonumber \\
\mathbf{\theta}_t &=& \mathbf{\theta}_{t-1} - \mathbf{v}_t \nonumber
\end{eqnarray}$$
Why Momentum
- In the high curvature directions, the gradients cancel each other out, so momentum dampens the oscillations.
- In the low curvature directions, the gradients point in the same direction, allowing the parameters to pick up speed.
- If the gradient is constant (i.e. the cost surface is a plane), the parameters will reach a terminal velocity of $$ -\frac{\alpha}{1-\gamma}\cdot \frac{\partial \mathcal{L}}{\partial \mathbf{\theta}} $$
- This suggests if you increase $\gamma$, you should lower $\alpha$ to compensate.
- Momentum sometimes helps a lot, and almost never hurts.
Ravines
- Even with momentum and normalization tricks, narrow ravines are still one of the biggest obstacles in optimizing neural networks.
- Empirically, the curvature can be many orders of magnitude larger in some directions than others!
- Second-order optimization develops algorithms which explicitly use curvature information (second derivatives), but these are complicated and difficult to scale to large neural nets and large datasets.
- Adam is an optimization algorithm that uses just a little bit of curvature information and often works much better than gradient descent.
Adam
- Adapt learning rate by using moments of gradients
- First and Second Order Moments: $$ \begin{eqnarray} \mathbf{m}_t &=& \beta_1 \mathbf{m}_{t-1} + (1-\beta_1)\mathbf{g}_t \\ \mathbf{v}_t &=& \beta_2 \mathbf{v}_{t-1} + (1-\beta_2)\mathbf{g}^2_t \end{eqnarray} $$
- Bias Correction: $$ \begin{eqnarray} \mathbf{\hat{m}}_t = \frac{\mathbf{m}_t}{1-\beta_1} \nonumber \\ \mathbf{\hat{v}}_t = \frac{\mathbf{v}_t}{1-\beta_2} \nonumber \end{eqnarray} $$
- Adam Update: $$ \begin{equation} \mathbf{\theta}_t = \mathbf{\theta}_{t-1} - \frac{\alpha}{\sqrt{\mathbf{\hat{v}}_t+\epsilon}}\mathbf{\hat{m}}_t \end{equation} $$
Adam Continued...
- Very commonly used, hundreds of thousands of papers.
- Adam with $\beta_1 = 0.9$, $\beta_2 = 0.999$, and learning_rate = 1e-3, 5e-4, 1e-4 is a great starting point for many models!
Optimization Algorithm Comparison
| Algorithm | Tracks 1st moments (momentum) | Tracks 2nd moments (adaptive LR) | Leaky 2nd moments | Bias correction for momentum updates |
|---|---|---|---|---|
| SGD | ||||
| SGD+Momentum | ||||
| Nesterov | ||||
| AdaGrad | ||||
| RMSProp | ||||
| Adam |
$L_2$ Regularization vs Weight Decay
- $\mathcal{L}(\mathbf{w})=\mathcal{L}_{data}(\mathbf{w})+\mathcal{L}_{reg}(\mathbf{w})$
- $\mathbf{g}_t = \nabla\mathbf{L}(\mathbf{w}_t)$
- $\mathbf{s}_t = optimizer(\mathbf{g}_t)$
- $\mathbf{w}_{t+1}=\mathbf{w}_t - \alpha\mathbf{s}_t$
- $L_2$ regularization and weight decay are equivalent for SGD and SGD+Momentum.
- But they are not the same for adaptive methods (AdaGrad, RMSprop, Adam etc.)
- Loshchilov and Hutter, “Decoupled Weight Decay Regularization”, ICLR 2019
- $\mathcal{L}(\mathbf{w})=\mathcal{L}_{data}(\mathbf{w})+\lambda\|\mathbf{w}\|_2^2$
- $\mathbf{g}_t = \nabla\mathbf{L}(\mathbf{w}_t)=\nabla\mathbf{L}_{data}(\mathbf{w}_t)+2\lambda\mathbf{w}$
- $\mathbf{s}_t = optimizer(\mathbf{g}_t)$
- $\mathbf{w}_{t+1}=\mathbf{w}_t - \alpha\mathbf{s}_t$
- $\mathcal{L}(\mathbf{w})=\mathcal{L}_{data}(\mathbf{w})$
- $\mathbf{g}_t = \nabla\mathbf{L}_{data}(\mathbf{w}_t)$
- $\mathbf{s}_t = optimizer(\mathbf{g}_t) + 2\lambda\mathbf{w}$
- $\mathbf{w}_{t+1}=\mathbf{w}_t - \alpha\mathbf{s}_t$
$L_2$ Regularization vs Weight Decay

- AdamW decouples weight decay.
- It should be your default optimizer
Believe when you see it...
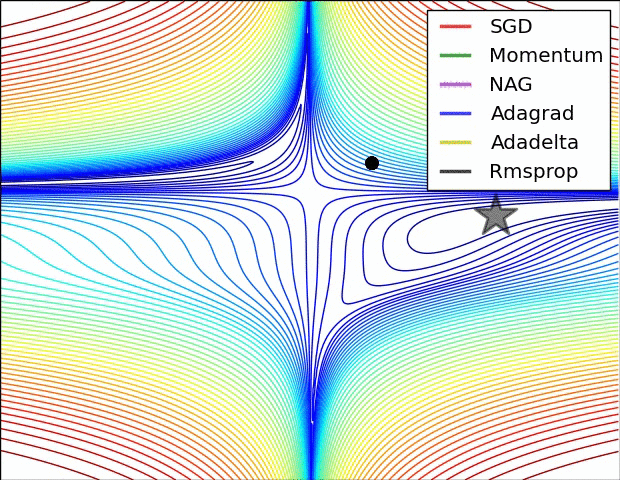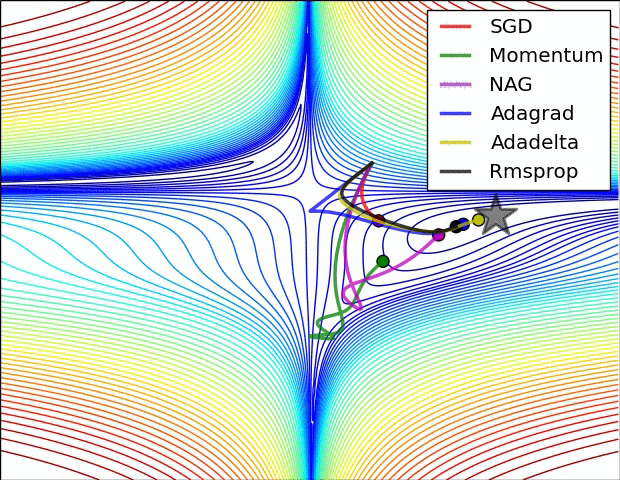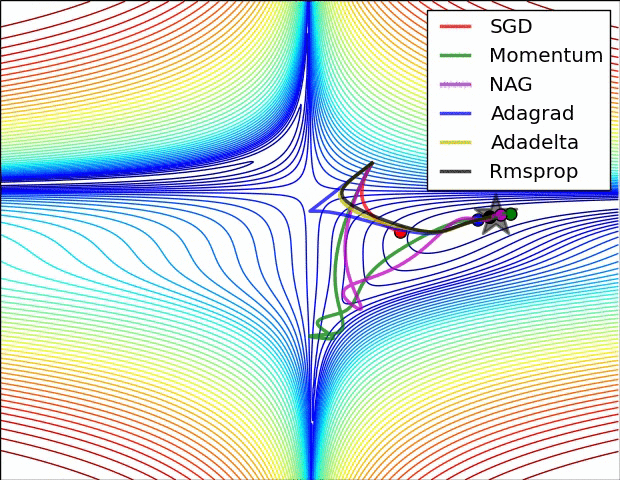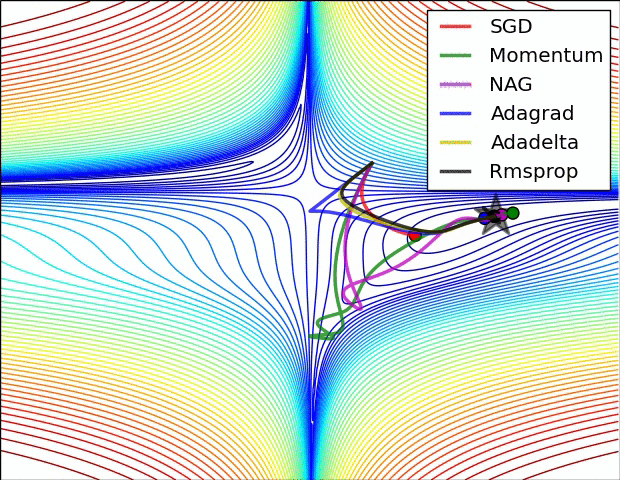
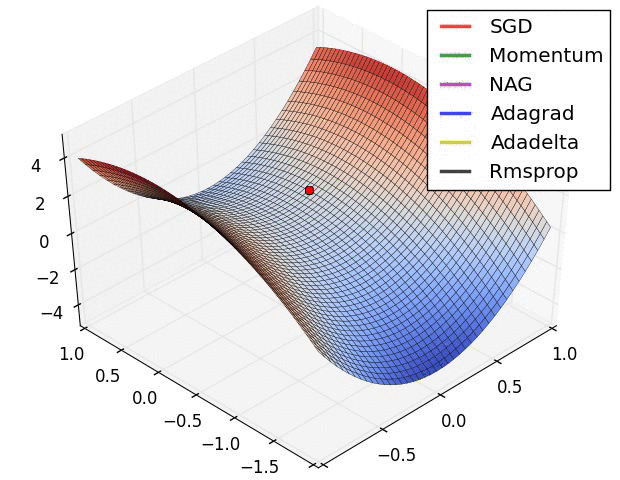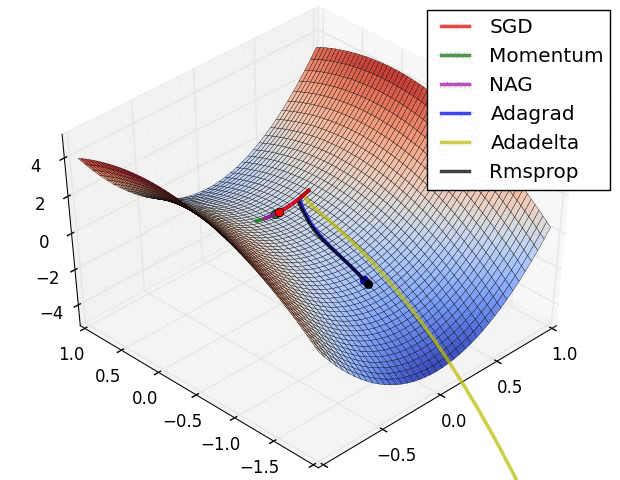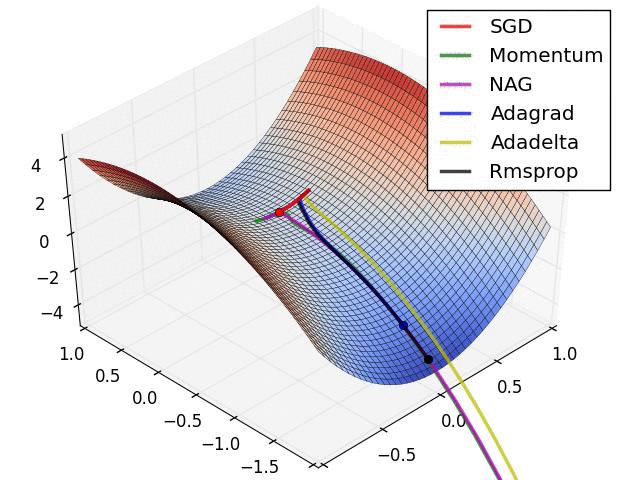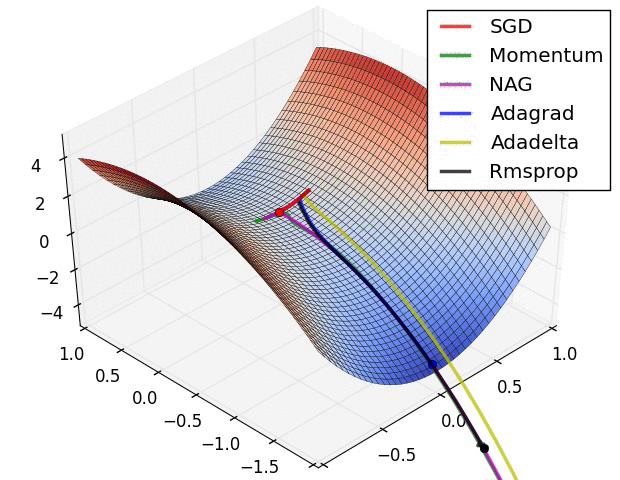
Second Order Gradient Descent
- Second Order Taylor Approximation: $$ \begin{eqnarray} f(\mathbf{x}) &=& f(\mathbf{x}_0) + (\mathbf{x}-\mathbf{x}_0)^T\nabla_{\mathbf{x}}f(\mathbf{x}_0) + \frac{1}{2}(\mathbf{x}-\mathbf{x}_0)^T\nabla^2_{\mathbf{x}}f(\mathbf{x}_0)(\mathbf{x}-\mathbf{x}_0) \nonumber \end{eqnarray} $$
- Newton Update: $$ \begin{eqnarray} \nabla_{\mathbf{x}}f(\mathbf{x}) &=& 0 \nonumber \\ \nabla_{\mathbf{x}}f(\mathbf{x}_0) + \nabla^2_{\mathbf{x}}f(\mathbf{x}_0)(\mathbf{x}-\mathbf{x}_0) &=& 0 \nonumber \\ \mathbf{x} &=& \mathbf{x}_0 - \left[\nabla^2_{\mathbf{x}}f(\mathbf{x}_0)\right]^{-1}\nabla_{\mathbf{x}}f(\mathbf{x}_0) \nonumber \end{eqnarray} $$
- Why is this impractical?
- Hessian has $\mathcal{O}(n^2)$ elements. Inverting takes $\mathcal{O}(n^3)$
Second Order Optimization
$\mathbf{x} = \mathbf{x}_0 - \left[\nabla^2_{\mathbf{x}}f(\mathbf{x}_0)\right]^{-1}\nabla_{\mathbf{x}}f(\mathbf{x}_0)$- Many approximations (quasi-newton methods) have been proposed in the literature (BFGS, L-BFGS etc.)
- BFGS: instead of inverting the Hessian $\mathcal{O}(n^3)$, approximate inverse Hessian with rank 1 updates over time ($\mathcal{O}(n^2)$ each)
- L-BFGS (limited memory BFGS): Does not form/store the full inverse Hessian
- Usually works very well in full batch, deterministic mode i.e. if you have a single, deterministic $f(x)$ then L-BFGS will probably work very nicely
- Does not transfer very well to mini-batch setting. Gives bad results. Adapting second-order methods to large-scale, stochastic setting is an active area of research.
In Practice...
- Adam/AdamW is a good default choice.
- In many cases SGD+Momentum can outperform Adam but may require more tuning.
- If you can afford to do full batch updates, then try out L-BFGS (remember to turn-off all sources of noise).
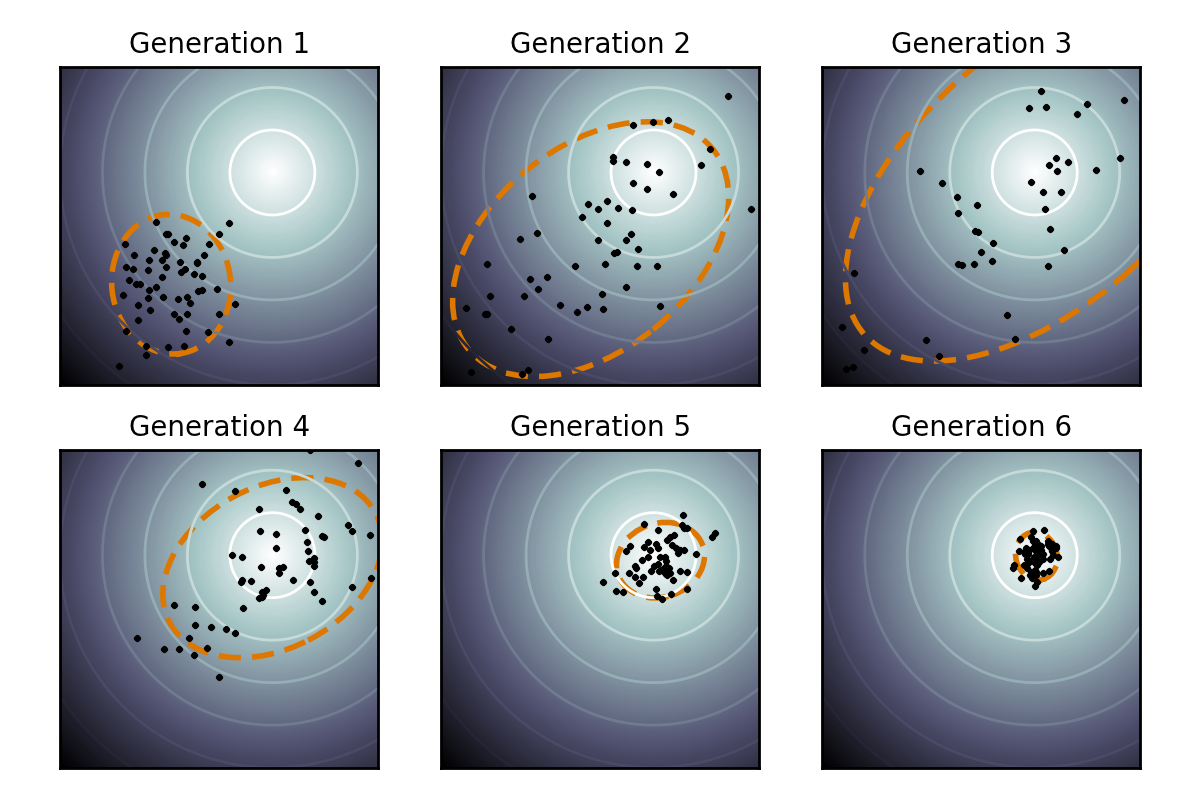
Covariance Matrix Adaptation Evolution Strategy (CMA-ES)
- Gradient Free Optimization
- Until convergence:
- Sample from Gaussian distribution around current location.
- Evaluate and sort function values
- Update mean and covariance of Gaussian distribution
Q & A