Graph Neural Networks - I
CSE 891: Deep Learning
Vishnu Boddeti
Traditional Neural Networks
- Deep neural networks that exploit:
- translational equivariance (weight sharing)
- heirarchical compositionality
- Data Domain:
- Images, volumes, videos lie on 2D, 3D, 2D+1 Euclidean domains (grids)
- Sentences, words, speech lie on 1D Euclidean domain
- These domains have strong regular spatial structures.
- All ConvNet operatiions are mathemtically well defined and fast (convolution, pooling)





Graphs in the Real-World
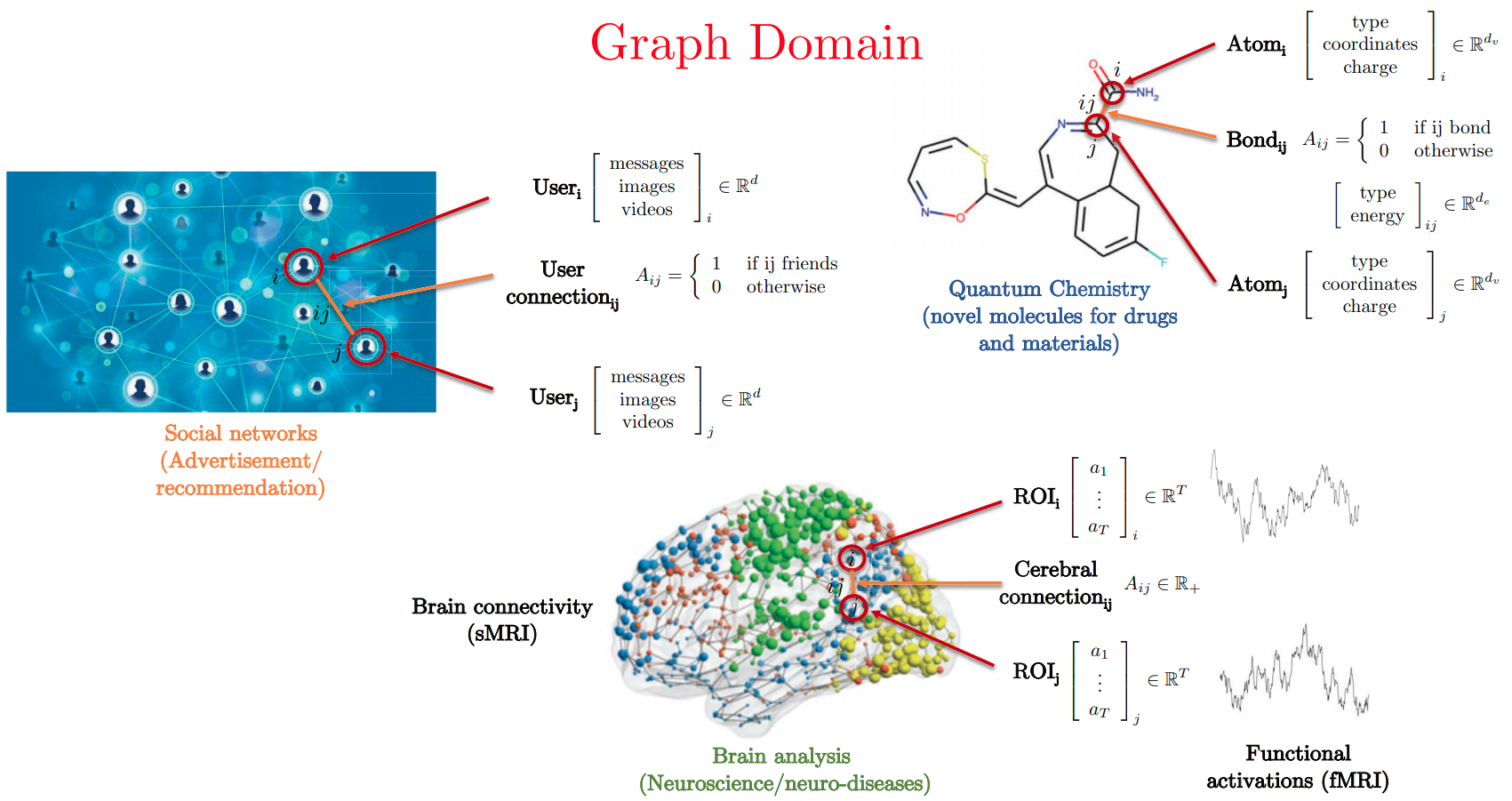
- Slide Credit: Xavier Bresson
Graph Structured Data

Standard CNN and RNN architectures don't work on this data.
- Slide Credit: Xavier Bresson
Molecules As Graphs
- Molecules can be represented by a graph
- Nodes: atoms
- Edges: bonds
- Features: atom type, charge, bond type
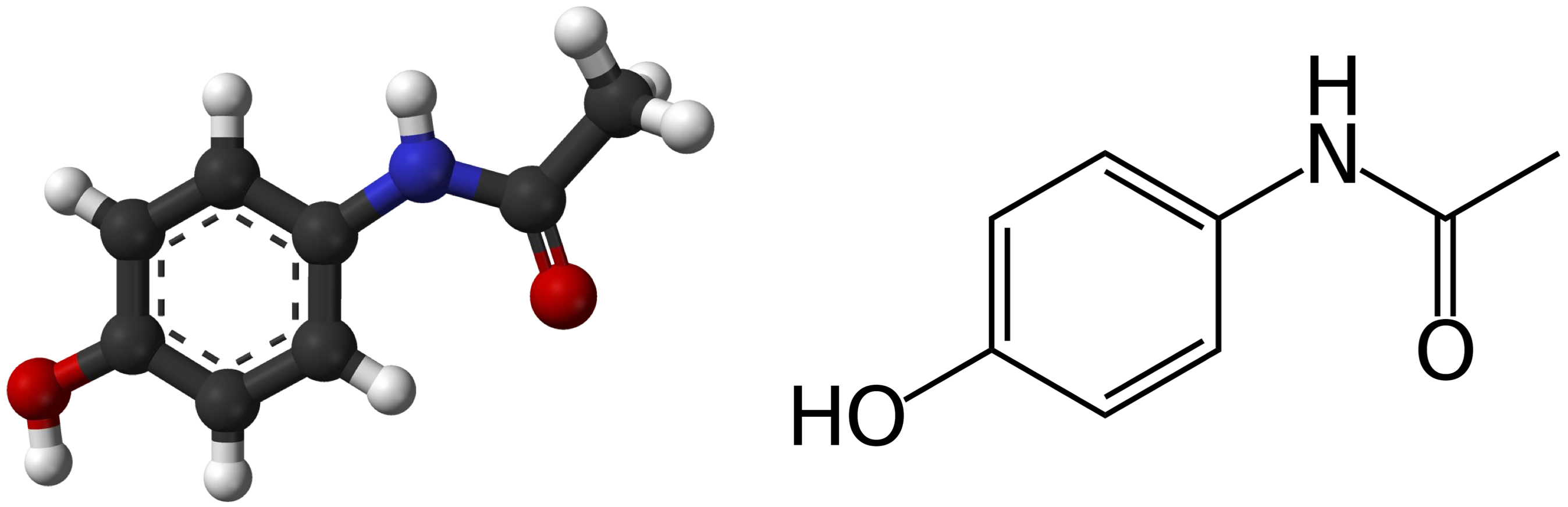
- Image Credit: Petar Veličković
GNN for Molecule Classification
- Task: predict whether a molecule is a potent drug
- binary classification to predict whether a drug will inhibit E.coli
- Train on curated dataset for molecules whose response is known
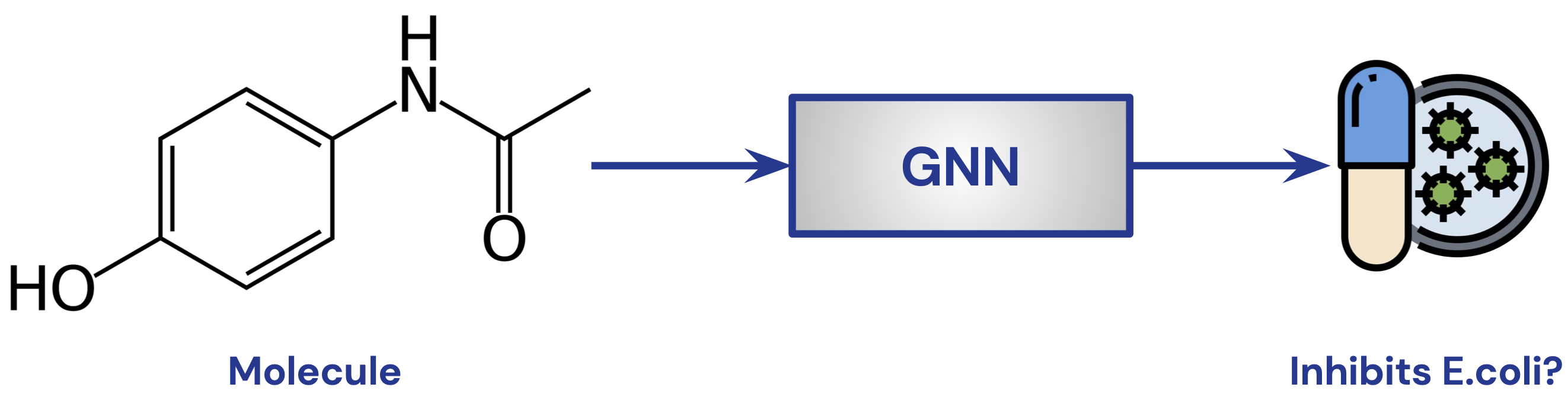
- Image Credit: Petar Veličković
Molecule: Real-World Success
- Once trained, GNN model can be applied to any molecule.
- Apply model on a large dataset of known candidate molecules
- Select the top 100 candidates from the GNN model
- manually evaluate selected candidates
- Success: discovered a previously overlooked compound that is a highly potent antibiotic

- A Deep Learning Approach to Antibiotic Discovery, Cell 2020
- Image Credit: Petar Veličković
Routing on Maps
- Transportation maps are naturally modelled as graphs
- Nodes: intersections
- Edges: roads
- Features: road length, current speed, historic speed

Routing on Maps
- Run GNN on supersegment graph to estimate time of arrival (graph regression)
- Already deployed in several major cities, significantly reduced negative ETA outcomes

GNNs from Scratch
Convolutional Neural Networks on Grids

- CNNs nicely exploit the grid structure of data.

- 2D convolutional operator as applied to a grid-structured input (e.g., image)
- What symmetries and invariances are preserved by CNNs?
- Invariance: CNNs respect translational invariance.
- Locality: Neighbouring pixels are related more strongly than far away pixels.
What about Graphs?
- What properties are useful for operating meaningfully on graphs?
- The nodes of a graph are not assumed to be in any order
- We would like to get the same results for two isomorphic graphs
- What symmetries and invariances must a GNN preserve?
- permutation invariance
- permutation equivariance

Learning on Sets
- Assume a set of nodes, without any edges.
- Let $\mathbf{x}_i \in \mathbb{R}^n$ be the feature of node $i$ i.e., $\mathbf{X}=(\mathbf{x}_1,\dots,\mathbf{x}_k)^T$
- we implicitly defined a node ordering
- would like our neural network to not depend on it
- Permutations change node-orderings.
- defined by a $n \times n$ permutation matrix
- has exactly one 1 in every row and column, and zeros everywhere else
- $\mathbf{X}' = \mathbf{P}\mathbf{X}$
Permutation Invariance
- Want to design $f(\mathbf{X})$ over sets that does not depend on the order.
- Want invariance to permutations i.e., for all permutation matrices $\mathbf{P}$:
- $f(\mathbf{PX})=f(\mathbf{X})$
- One very generic form is the Deep Sets model (Zaheer et al., NeurIPS 2017): $$f(\mathbf{X})=\phi\left(\sum_{i\in\mathcal{V}}\psi(\mathbf{x})\right)$$
- $\phi$ and $\psi$ are learnable functions, e.g., MLPs
- the sum is critical (other choices are max and avg)
Permutation Equivariance
- Permutation-invariance is good for obtaining set-level outputs
- In many problems we want node level predictions.
- need to identify node outputs, but permutation-invariant aggregator destroys it
- Need functions that doesn't change node order
- We need $f(\mathbf{X})$ to be permutation-equivariant, for all permutation matrices: $$f(\mathbf{PX})=\mathbf{P}f(\mathbf{X})$$
Learning on Sets
- Equivariance mandates that each node’s row is unchanged by f.
- equivariant set functions transform each node $\mathbf{x}_i$ into a latent vector $\mathbf{h}_i$ $$\mathbf{h}_i=\psi(\mathbf{x}_i)$$
- $\psi(\cdot)$ is applied to each node
- stacking $\mathbf{h}_i$ yields $H=f(\mathbf{X})$
- Recipe: combine equivariant functions with invariant functions $$f(\mathbf{X})=\phi\left(\bigoplus_{i\in\mathcal{V}}\psi(\mathbf{x}_i)\right)$$
- $\bigoplus$ is a permutation invariant operator (e.g., sum, max, avg)
Learning on Graphs
- Graphs $\mathcal{G}$ are defined by:
- Vertices $V$
- Edges $E$
- Adjacency matrix $\mathbf{A}$ $$a_{ij} = \begin{cases} 1 \quad (i,j)\in\mathcal{E} \\ 0 \quad otherwise \end{cases}$$
- Features:
- Node features: $\mathbf{h}_i, \mathbf{h}_j$ (user type)
- Edge features: $\mathbf{e}_{ij}$ (relation type)
- Graph features: $\mathbf{g}$ (network type)

- We want our main desiderata, permutation invariance and permutation equivariance, to still hold
Permutation Invariance and Equivariance on Graphs
- Key Difference: node permutations act accordingly on the edges
- Need to permute both rows and columns of $\mathbf{A}$
- apply permutation matrix as $\mathbf{PAP}^T$
- Invariant and equivariant functions $f(\mathbf{X},\mathbf{A})$ on graphs:
- Invariance: $f(\mathbf{PX},\mathbf{PAP}^T)=f(\mathbf{X},\mathbf{A})$
- Equivariance: $f(\mathbf{PX},\mathbf{PAP}^T)=Pf(\mathbf{X},\mathbf{A})$
Locality on Graphs
- On sets, equivariance was enforced by applying functions to every node in isolation.
- On graphs, broader context is given by a node's neighbourhood
- For a node $i$, we can define its (1-hop) neighbourhood as: $$\mathcal{N}_i=\{j: (i,j)\in\mathcal{E} \vee (j,i) \in \mathcal{E}\}$$
- We can extract a multiset of features in the neighborhood $$\mathbf{X}_{\mathcal{N}_i}=\{\{\mathbf{x}_j: j\in \mathcal{N}_i\}\}$$
- define a local function $g$ that operates on the multiset $g(\mathbf{x}_i, \mathbf{X}_{\mathcal{N}_i})$
How to use GNNs?
Recipe for graph neural networks
- Construct permutation equivariant functions, $f(\mathbf{X},\mathbf{A})$, by appropriately applying a local function, $g$, over all neighbourhoods: $$f(\mathbf{X}, \mathbf{A})=\begin{bmatrix} - & g(\mathbf{x}_1, \mathbf{X}_{\mathcal{N}_1}) & - \\ - & g(\mathbf{x}_2, \mathbf{X}_{\mathcal{N}_2}) & - \\ & \vdots & \\ - & g(\mathbf{x}_n, \mathbf{X}_{\mathcal{N}_n}) & - \end{bmatrix}$$
- For equivariance, we ensure $g$ does not depend on order of the vertices in $\mathbf{X}_{\mathcal{N}_i}$
- i.e., $g$ should be permutation invariant
Recipe for graph neural networks

GNN Pipeline
- Standard GNN Pipeline:
- Input Layer: Linear embedding of input node/edge features.
- GNN Layers: Apply favorite GNN layer $L$ times.
- Task-based layer : Graph/node/edge prediction layer.

GNN Pipeline
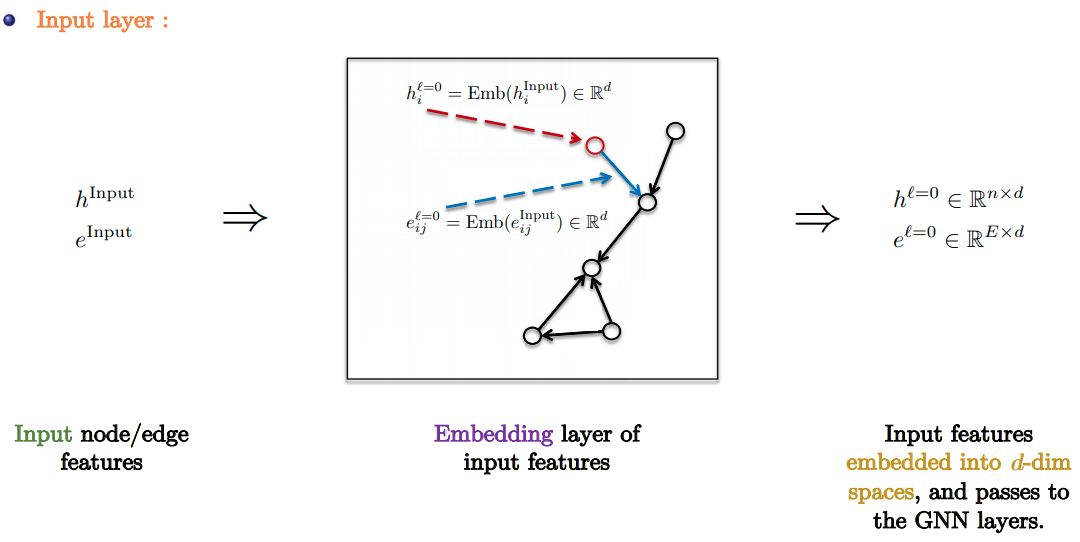
- Slide Credit: Xavier Bresson
GNN Pipeline
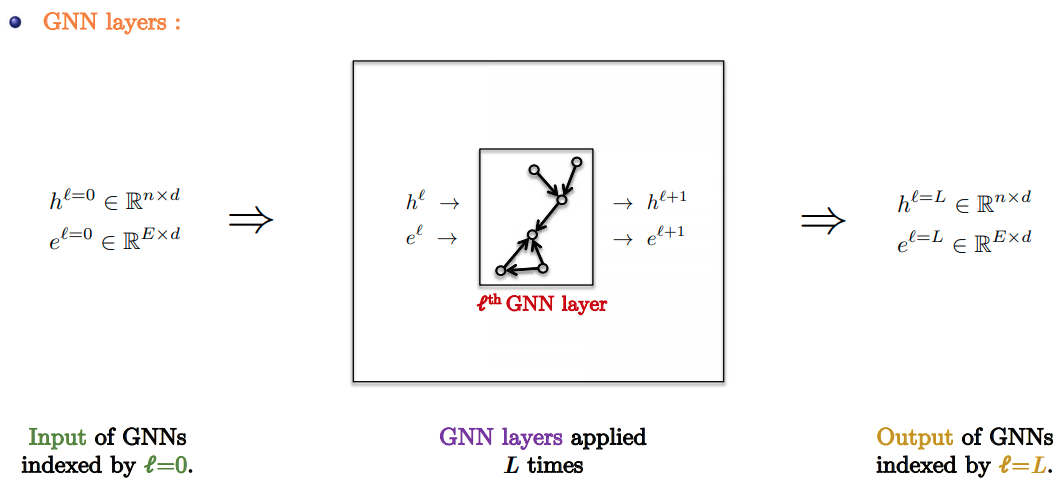
- Slide Credit: Xavier Bresson
GNN Pipeline

- Slide Credit: Xavier Bresson