Fairness in AI
CSE 891: Deep Learning
Vishnu Boddeti
Progress In Machine Learning
Speech Processing
Image Analysis
Natural Language Processing
Physical Sciences
State-of-Affairs
(report from the real-world)
March 24, 2016


April 25, 2017


Feb. 09, 2018


- Boulamwini and Gebru, "Gender Shades:Intersectional Accuracy Disparities in Commercial Gender Classification," FAT 2018

Jan. 18, 2020

What We Need?
100 Years of Data Representations




Bias in Learning
- Training:
- Inference: Microsoft Gender classification


- Boulamwini and Gebru, "Gender Shades:Intersectional Accuracy Disparities in Commercial Gender Classification," FAT 2018
Economic Bias

- DeVries "Does Object Recognition Work for Everyone?," CVPRW 2020
Recklessly absorb all statistical correlations in data
Next Era of Learned Representations


What is Algorithmic Fairness?
The Many Faces of Fairness
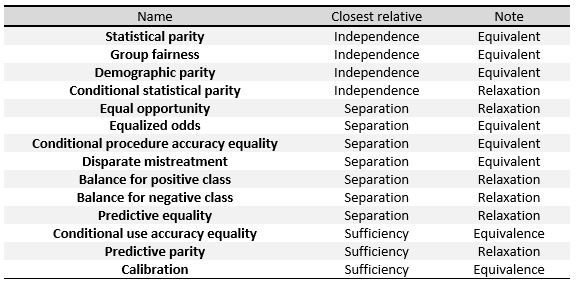
- Main classes for fairness definitions:
- Independence: $\hat{Y} \perp \!\!\! \perp S$
- Separation: $\hat{Y} \perp \!\!\! \perp S | Y$
- Sufficiency: $Y \perp \!\!\! \perp S | \hat{Y}$
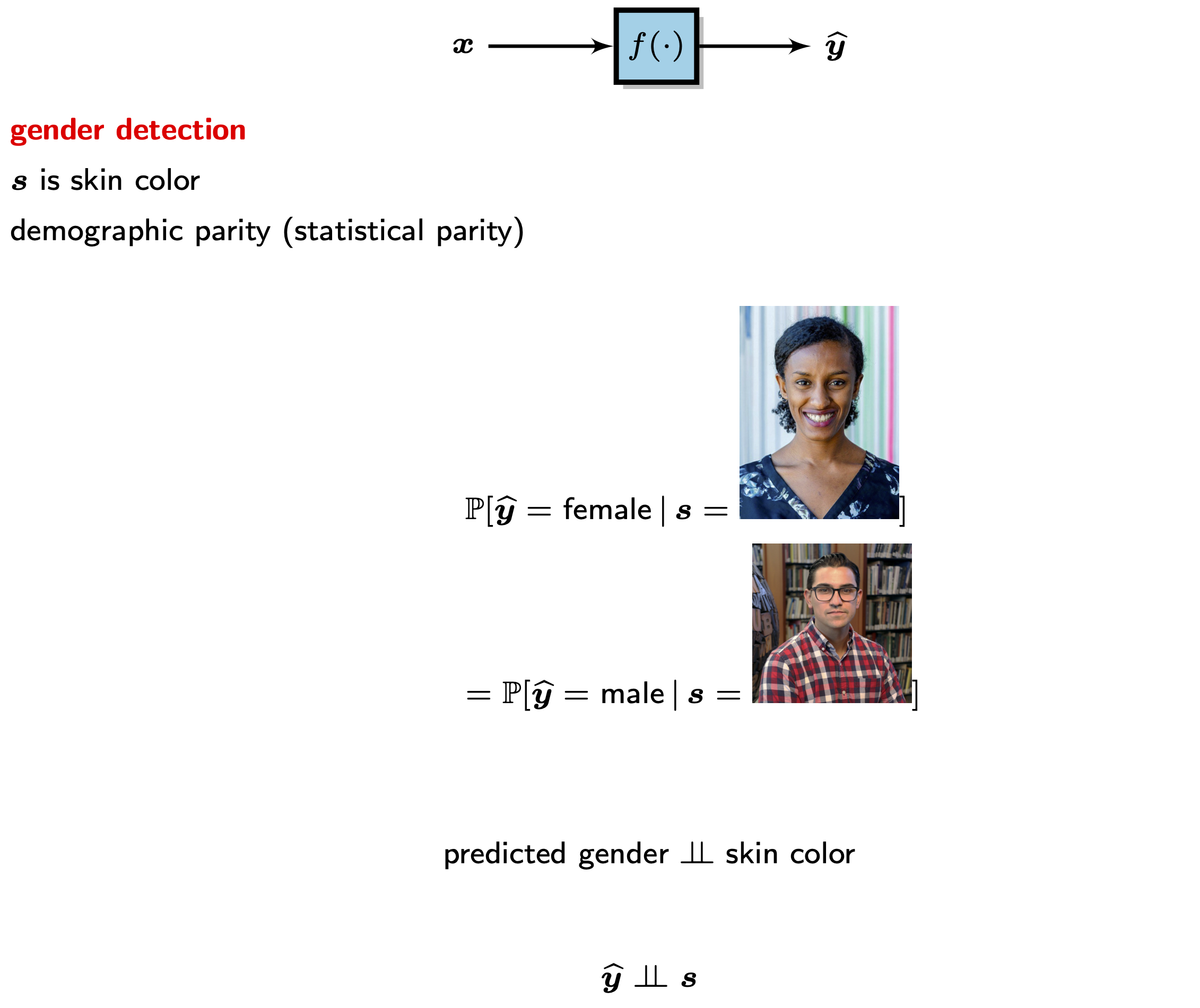
DemographiC Parity
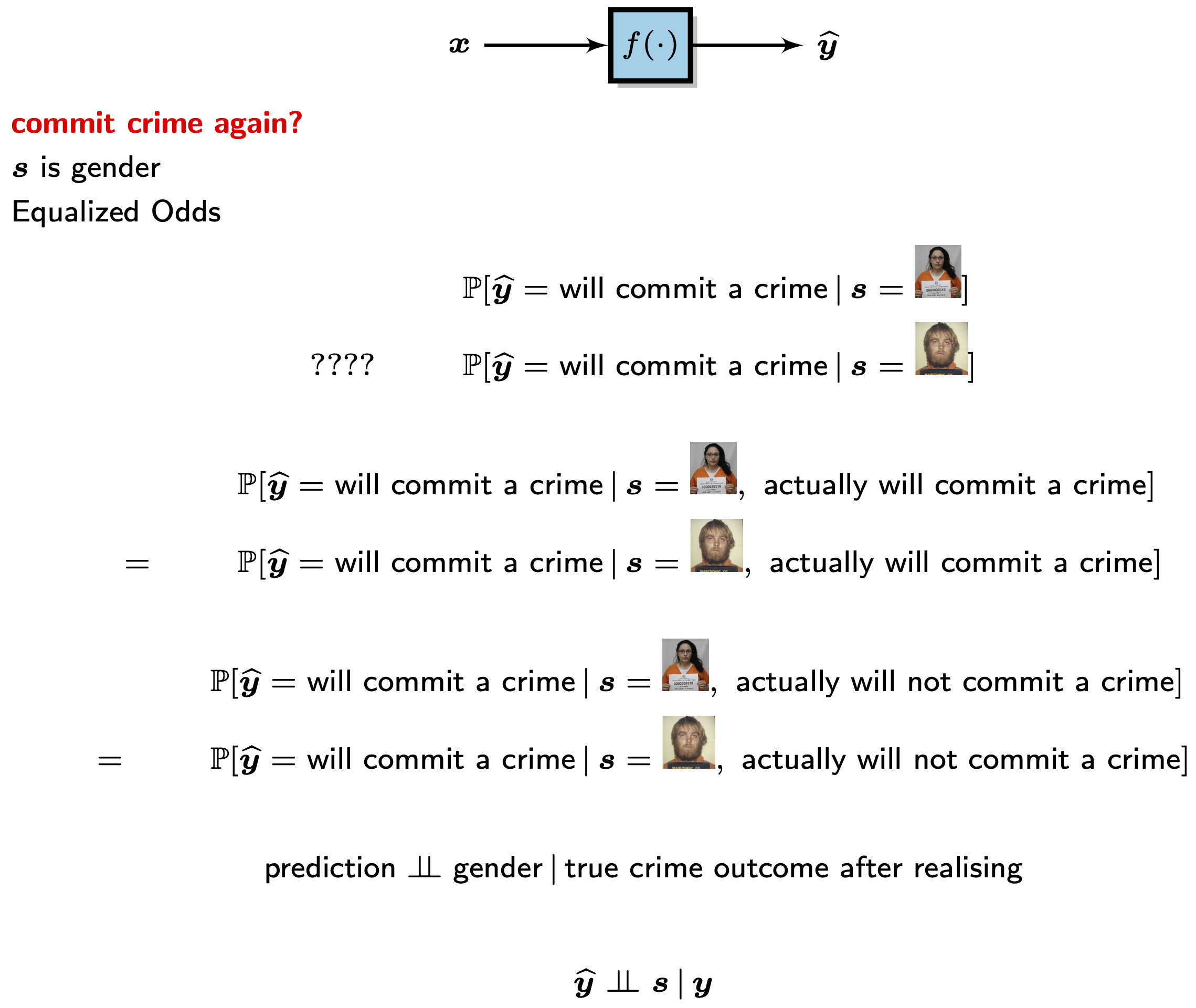
Equalized Odds
Equality of Opportunity

Individual Fairness: Treat similar individuals similarly

- Pairs of similar individuals playing the same sport classified differently.
- Stock and Cisse, 2018
Fairness Overview
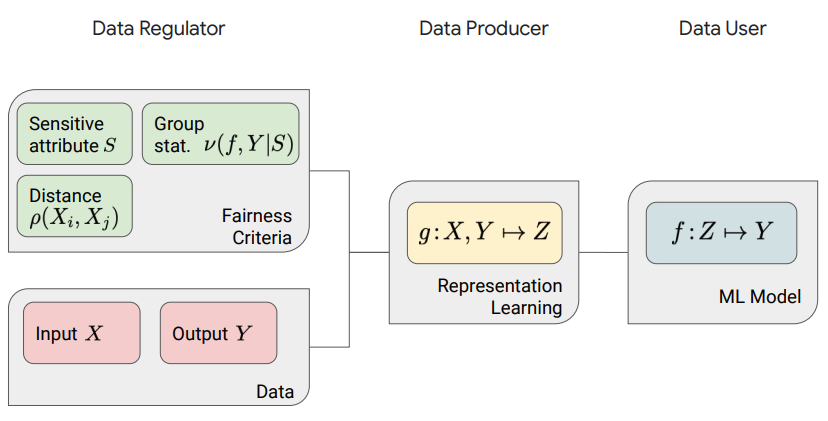
- Source: Sanmi Koyejo
Fair Representation Learning
Fair Representation Learning
- Target Concept: Smile & Private Concept: Gender
- Problem Definition:
- Learn a representation $\mathbf{z} \in \mathbb{R}^d$ from data $\mathbf{x}$
- Retain information necessary to predict target attribute $\mathbf{t}\in\mathcal{T}$
- Remove information related to a desired sensitive attribute $\mathbf{s}\in\mathcal{S}$



Technical Challenge
- How to explicitly control semantic information in learned representations?
- Can we explicitly control semantic information in learned representations?
A Subspace Geometry Perspective
- Case 1: when $\mathcal{S} \perp \!\!\! \perp \mathcal{T}$ (Gender, Age)


- Case 3: when $\mathcal{S} \sim \mathcal{T}$ ($\mathcal{T}\subseteq\mathcal{S}$)

- Case 2: when $\mathcal{S} \not\perp \!\!\! \perp \mathcal{T}$ (Car, Wheels)





- B. Sadeghi, L. Wang, V.N. Boddeti, "Adversarial Representation Learning with Closed-Form Solutions," CVPRW 2020
Trade-Offs in Fair Representation Learning

- Sadeghi, Dehdastian and Boddeti, On Characterizing the Trade-off in Invariant Representation Learning, TMLR 2022
A Fork in the Road
- Design metric to measure semantic attribute information
- use dependence measures
- Learn metric to measure semantic attribute information
- probably feasible
Game Theoretic Formulation



- Three player game between:
- Encoder extracts features $\mathbf{z}$
- Target Predictor for desired task from features $\mathbf{z}$
- Adversary extracts sensitive information from features $\mathbf{z}$
- Adversary: learned measure of semantic attribute information
- Unsupervised domain adaptation by backpropagation, ICML 2015 and Controllable invariance through adversarial feature learning, NeurIPS 2017 and Mitigating information leakage in image representations: A maximum entropy approach, CVPR 2019 and many more
How do we learn model parameters?




- Simultaneous/Alternating Stochastic Gradient Descent
- Update target while keeping encoder and adversary frozen.
- Update adversary while keeping encoder and target frozen.
- Update encoder while keeping target and adversary frozen.
Three Player Game: Linear Case

- Global solution is $(w_1, w_2, w_3)=(0, 0, 0)$
- ARL exhibits strong rotation around fixed point.
Mitigation Strategies
- Non-Zero Sum Formulation for Iterative Methods (CVPR'19)
- Standard setting, each player is a deep neural network.
- Local optima
- Global Optima for Kernel Methods (ICCV'19)
- Simplified setting, each player is linear.
- closed form solution + stable + performance bounds
- Hybrid Model with CNNs and Closed-Form Solvers (ECML'21)
- Standard setting, encoder is a deep neural network, other players are closed-form solvers.
- Local optima
Optimizing Likelihood Can be Sub-Optimal



- Limitations:
- Encoder target distribution leaks information !!
- Practice: simultaneous SGD does not reach equilibrium
- Class Imbalance: likelihood biases solution to majority class
- P. Roy, V.N. Boddeti, "Mitigating Information Leakage in Image Representations: A Maximum Entropy Approach," CVPR 2019
Maximum Entropy Adversarial Representation Learning
Encoder optimizes entropy of adversary instead of likelihood.



Converges to Local Optima
- P. Roy, V.N. Boddeti, "Mitigating Information Leakage in Image Representations: A Maximum Entropy Approach," CVPR 2019
Maximum Entropy ARL Continued...



- Three player game between:
- Encoder extracts features $\mathbf{z}$
- Target Predictor for desired task from features $\mathbf{z}$
- Adversary extracts sensitive information from features $\mathbf{z}$
- Three Player Non-Zero Sum Game:
\begin{equation}
\begin{aligned}
\min_{\mathbf{\theta}_A} & \mbox{ } \underbrace{\color{orange}{J_1(\mathbf{\theta}_E,\mathbf{\theta}_A)}}_{\color{orange}{\mbox{error of adversary}}} \\
\min_{\mathbf{\theta}_E,\mathbf{\theta}_T} & \mbox{ } \underbrace{\color{cyan}{J_2(\mathbf{\theta}_E,\mathbf{\theta}_T)}}_{\color{cyan}{\mbox{error of target}}} - \alpha \underbrace{\color{orange}{J_3(\mathbf{\theta}_E,\mathbf{\theta}_A)}}_{\color{orange}{\mbox{entropy of adversary}}} \nonumber
\end{aligned}
\end{equation}
- P. Roy, V.N. Boddeti, "Mitigating Information Leakage in Image Representations: A Maximum Entropy Approach," CVPR 2019
Geometry of Optimization
\begin{equation} \begin{aligned} \min_{\mathbf{\Theta}_E} & \ \ {\color{cyan}{J_t(\mathbf{\Theta}_E)}} \\ \mathrm {s.t. \ \ } & {\color{orange}{J_s (\mathbf{\Theta}_E) \ge \alpha}} \nonumber \end{aligned} \end{equation}



- Non-convexity: feasible set is non-convex
- Non-differentiability: solution is either a plane or a line
- B. Sadeghi, R. Yu, V.N. Boddeti, ‘‘On the Global Optima of Kernelized Adversarial Representation Learning," ICCV 2019
Solution: Spectral Adversarial Representation Learning
- Lagrangian formulation: \begin{equation} \min_{\mathbf{\Theta}_E} \Big\{(1-\lambda){\color{cyan}{J_t(\mathbf{\Theta}_E)}}- (\lambda) {\color{orange}{J_s (\mathbf{\Theta}_E)} }\Big\} \nonumber \end{equation}
Non-Convex + Non-Differentiable
- Solution: \begin{equation} \mathbf{\Theta}_E, r^*=\mbox{Negative Eig} \Big\{\mathbf{X}\left(\lambda \color{orange}{\mathbf{S}^T \mathbf{S}} - (1-\lambda)\color{cyan}{\mathbf{Y}^T \mathbf{Y}} \right)\mathbf{X}^T \Big\}\nonumber \end{equation}
Global Optima + Optimal Dimensionality + Performance Bounds
- B. Sadeghi, R. Yu, V.N. Boddeti, "On the Global Optima of Kernelized Adversarial Representation Learning," ICCV 2019
Closed-Form Solvers



- Encoder extracts features $\mathbf{z}$
- Target Predictor: kernel ridge regressor to predict target from $\mathbf{z}$
- Adversary: kernel ridge regressor to extract sensitive information from $\mathbf{z}$
- B. Sadeghi, L. Wang, V.N. Boddeti, "Adversarial Representation Learning with Closed-Form Solutions," ECML 2021
Beyond ARL: Universal Dependence Measures
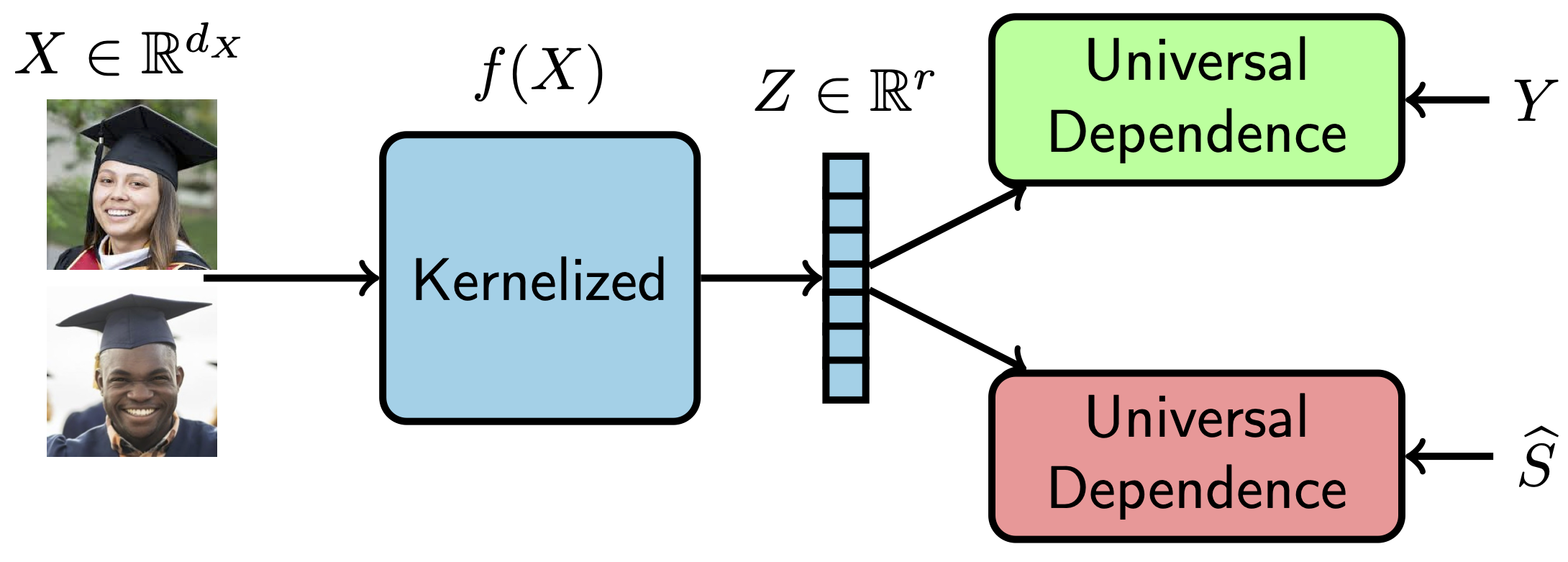

- Use covariance-based measures as dependency (e.g., HSIC, KCC)
- B. Sadeghi, S. Dehdastian, V.N. Boddeti, "On Characterizing the Trade-off in Invariant Representation Learning," TMLR 2022
Properties of Ideal Embedding

- Embedding Dimensionality
- # of negative eigenvalues of \begin{equation} \mathbf{B} = \lambda \tilde{\mathbf{S}}^T \tilde{\mathbf{S}} -(1-\lambda)\tilde{\mathbf{Y}}^T \tilde{\mathbf{Y}} \end{equation}

Practical Applications
Application-1: Fair Classification
- UCI Adult Dataset (creditworthiness, gender)
| Method | Income | Gender | $\Delta^*$ |
|---|---|---|---|
| Raw Data | 84.3 | 98.2 | 22.8 |
| Remove Gender | 84.2 | 83.6 | 16.1 |
| Zero-Sum game | 84.4 | 67.7 | 0.3 |
| Non-Zero-Sum Game | 84.6 | 67.3 | 0.1 |
| Global-Optima | 84.1 | 67.4 | 0.0 |
| Hybrid | 83.8 | 67.4 | 0.0 |
Fair Classification: Interpreting Encoder Weights

Application-2: Fair Representations for Faces


- CelebA Dataset (high cheekbone, (gender, age))
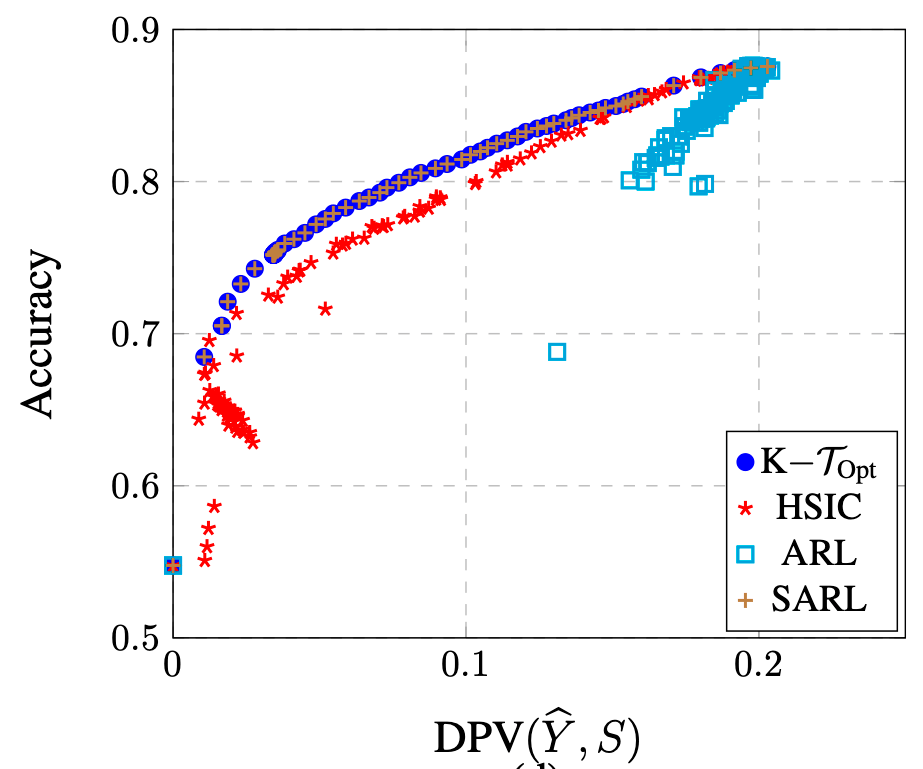
Application-3: Fair in Folktables Dataset (US Census)
- Washington State (employment status (binary), age)

- New York State (employment status (4 classes), age)

Summary
- Fairness is a nuanced and challenging issue with many open problems.
- Bias in ML system can be affected by all parts of the ML pipeline: data, neural network model, loss functions
- Representation learning is a promising approach for implementing algorithmic fairness
- Fair representation learning can be implemented with modular separation between tasks/roles:
- Data regulator: determines fairness measures, audits results
- Data producer: learns the fair representation
- Data user: agnostically learns the ML model
Lots of Open Questions
- For the data regulator:
- How does one pick appropriate fairness definitions?
- What are the best practices for auditing results?
- For the data producer:
- Can we improve algorithms for learning fair representations?
- Can one construct algorithms for individually fair representation learning?
- For the data user:
- What is the cost of fairness via representation learning?
- What are the best practices for avoiding fairness leakage?
- Many more algorithmic questions:
- What are the fundamental trade-offs between utility and fairness?
- What are the achievable trade-offs between utility and fairness?
