Course Review
CSE 891: Deep Learning
Vishnu Boddeti
DNN Design Involves...













Many More $\Huge \dots$
Deep Generative Models
- Goal: modeling $p_{data}$




What is Next?
New Types of Deep Models
Physics Informed Neural Networks: Motivation
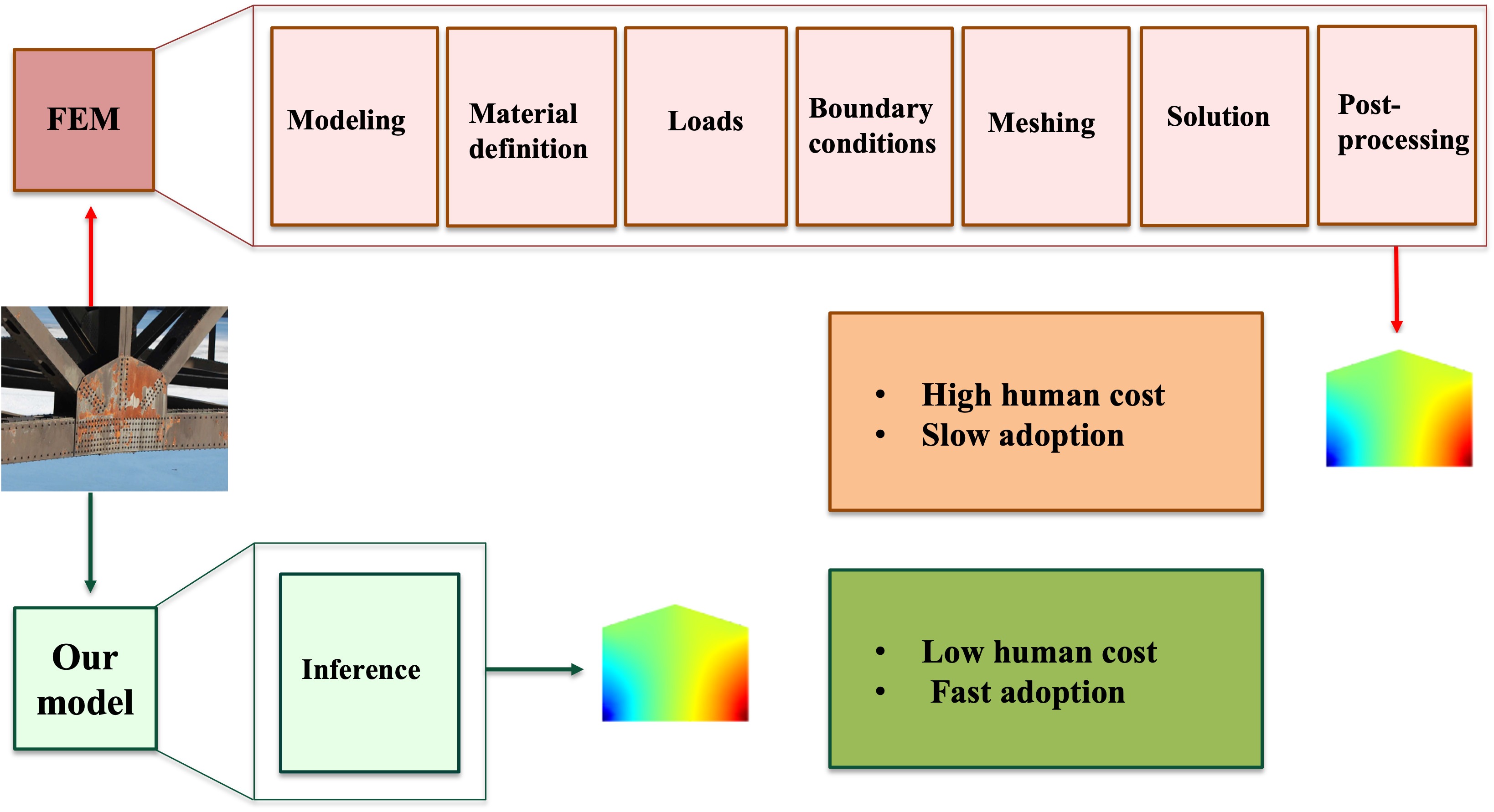
PINNs: Scenarios
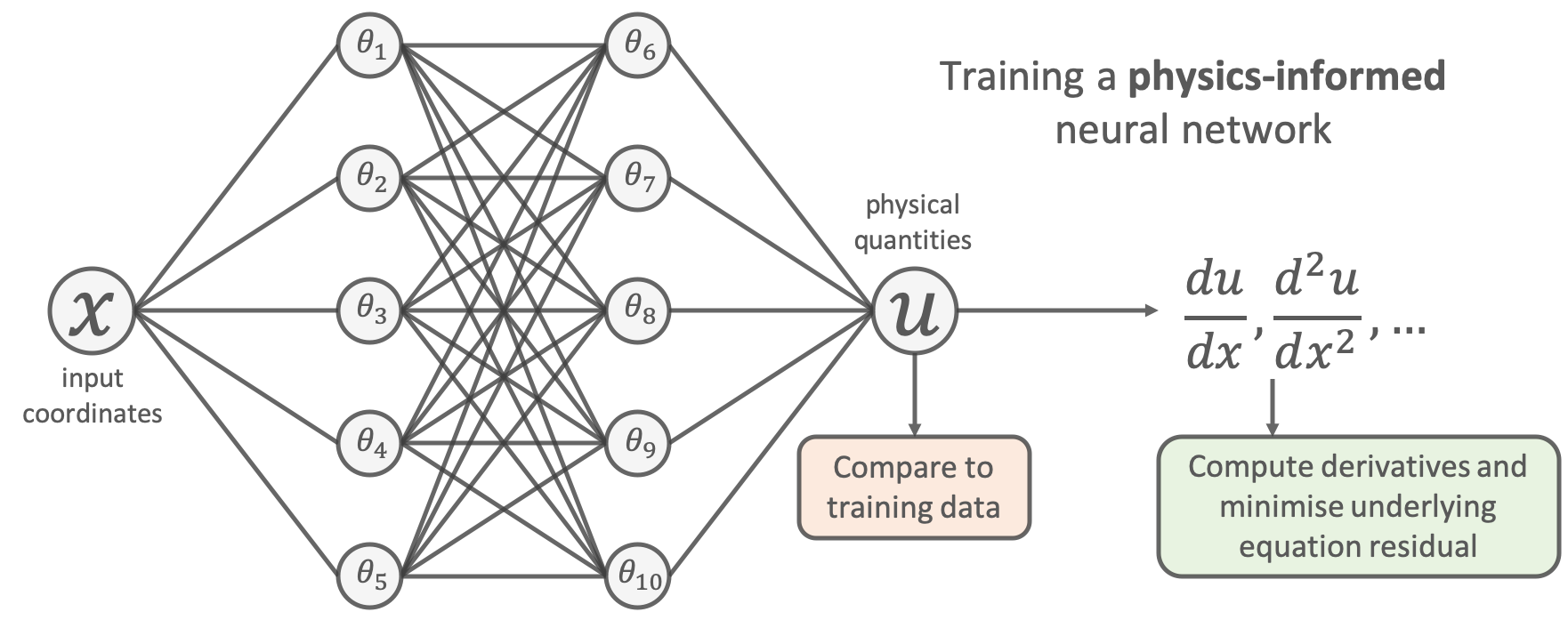
Direct Application of Neural Networks
- Purely data-driven approaches $$\min \frac{1}{N}\sum_{i=1}^N \left(u_{NN}(x_i;\theta) - u_{true}(x_i)\right)^2$$


- Figure Credit: https://benmoseley.blog
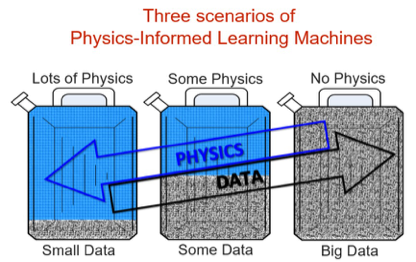
Physics Informed Neural Networks

- $$m\frac{d^2u}{dx^2}+\mu\frac{du}{dx}+ku=0$$

- $$ \begin{aligned} \min & \frac{1}{N}\sum_{i=1}^N\left(u_{NN}(x_i;\theta)-u_{true}(x_i)\right)^2 \\ & + \frac{1}{M}\sum_{j=1}^M \left(\left[m\frac{d^2}{dx^2}+\mu\frac{d}{dx}+k\right]u_{NN}(x_k;\theta)\right) \end{aligned} $$
Physics Informed Neural Networks
$$ \begin{equation} \begin{aligned} \frac{\partial u}{\partial t} + \beta\frac{\partial u}{\partial x} &= 0 \quad x \in \Omega, t\in[0,T] \\ u(x,0) &= h(x), \quad x \in \Omega \end{aligned} \end{equation} $$
- Raissi et al, ”Physics Informed Deep Learning: Data-driven Solutions of Nonlinear Partial Differential Equations.”, Arxiv 2017
- Krishnapriyan et al, ”Characterizing possible failure modes in physics-informed neural networks”, NeurIPS 2021
Fourier Neural Operators
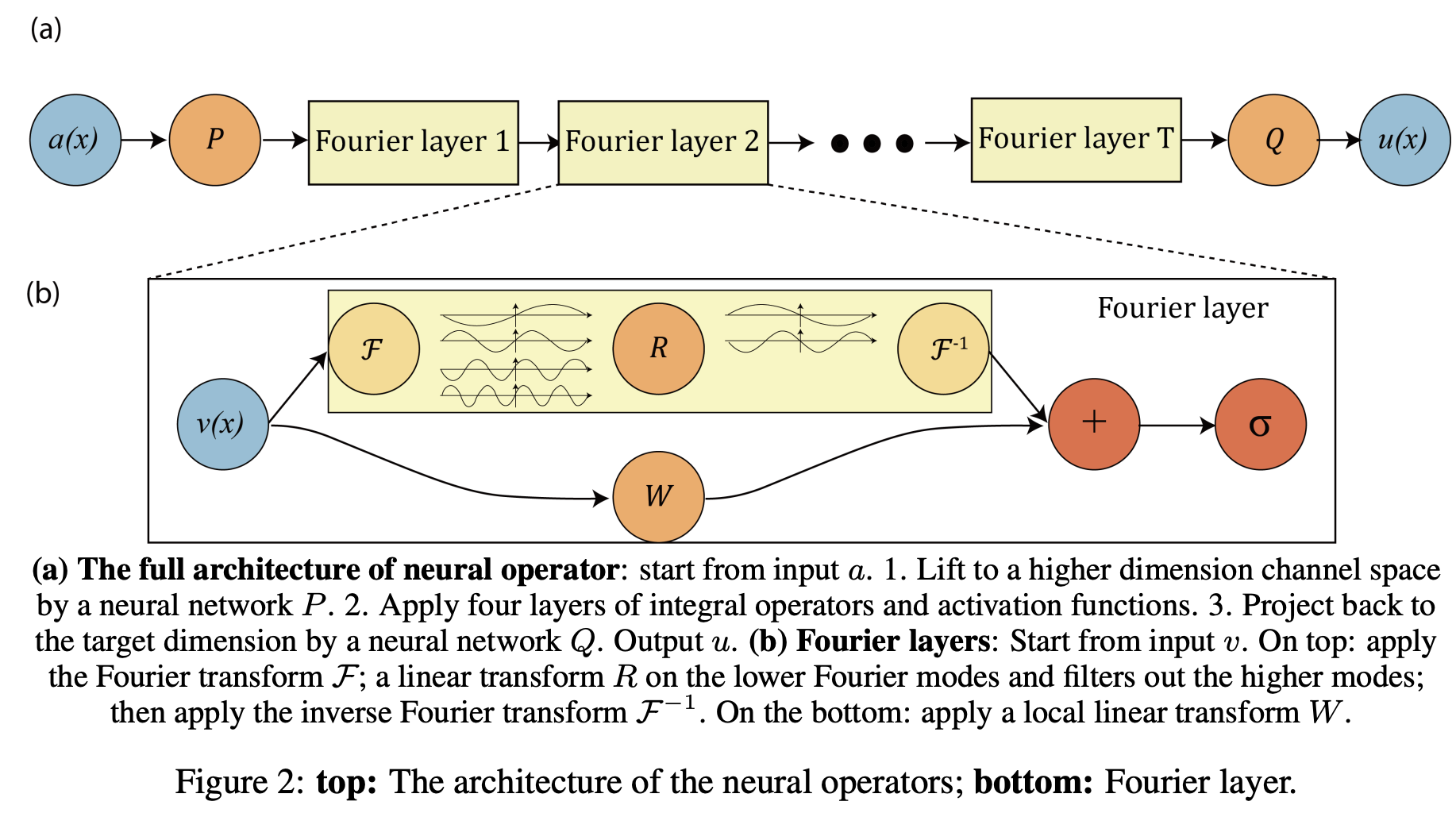
- Li et al, ”Fourier Neural Operator for Partial Differential Equations”, ICLR 2021
Fourier Neural Operators
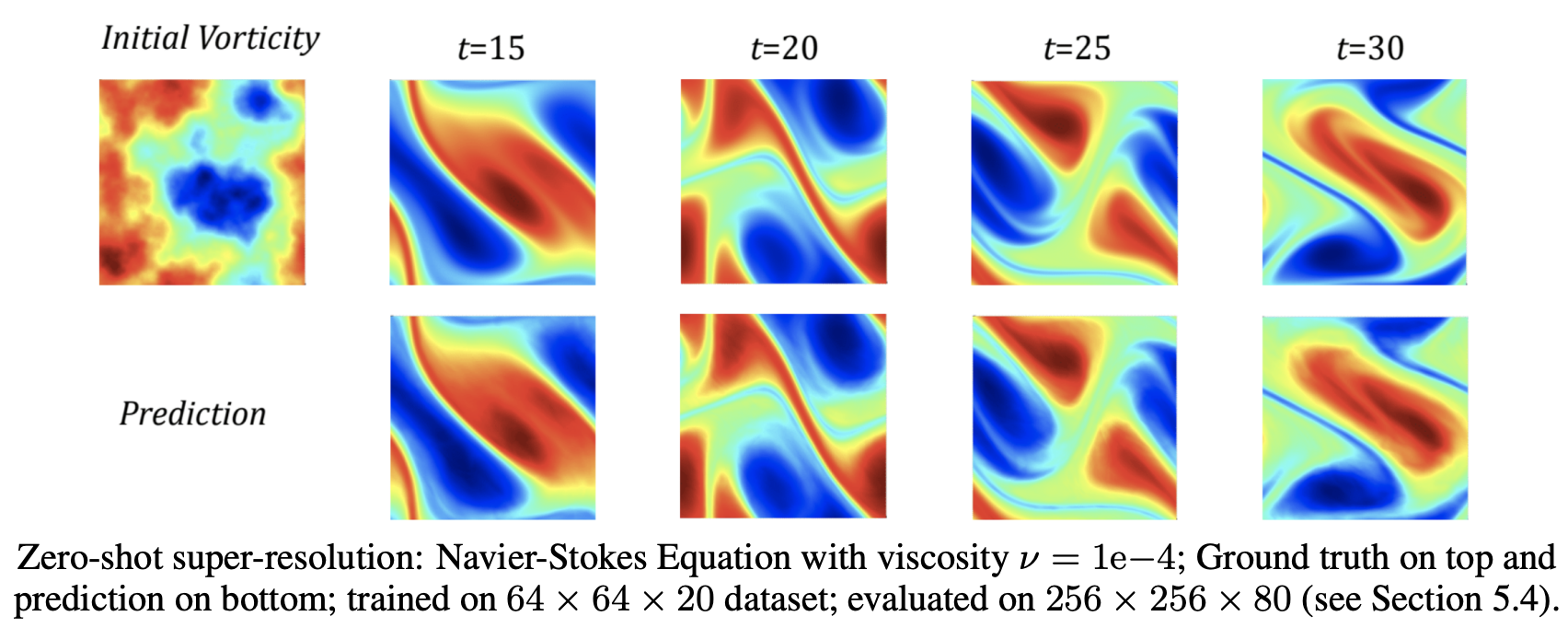
- Li et al, ”Fourier Neural Operator for Partial Differential Equations”, ICLR 2021
Neural ODEs
- Residual Network: $h_{t+1}=h_t + f(h_t,\theta)$
- Looks kind of like numerical integration.
- Neural ODE: Hidden states are solutions of: $\frac{dh}{dt}=f(h(t),t,\theta)$
- A deep network with infinitely many layers!
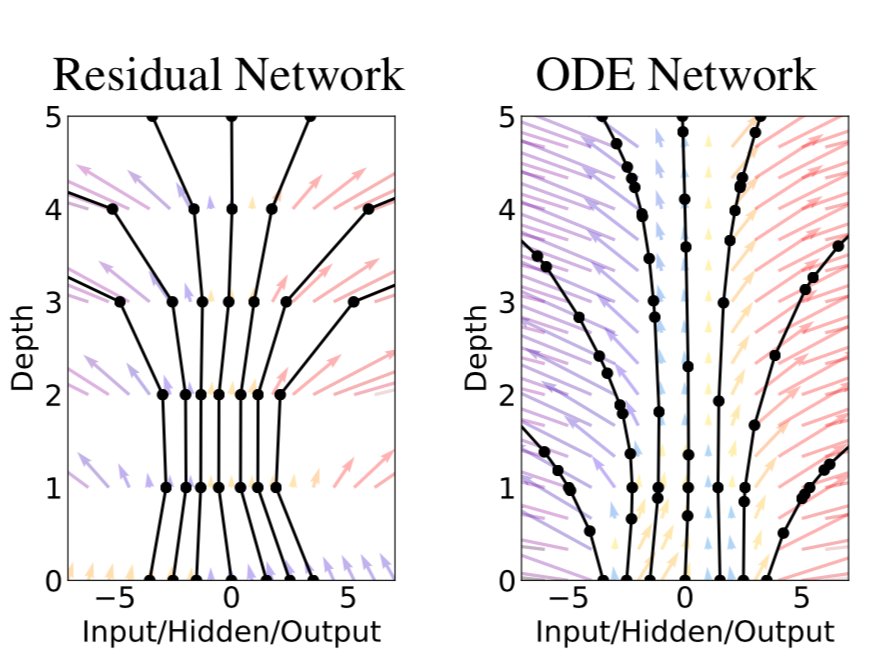
- Chen et al, ”Neural Ordinary Differential Equations”, NeurIPS 2018
New Applications of Deep Learning
Deep Learning for Graphics: NVIDIA DLSS
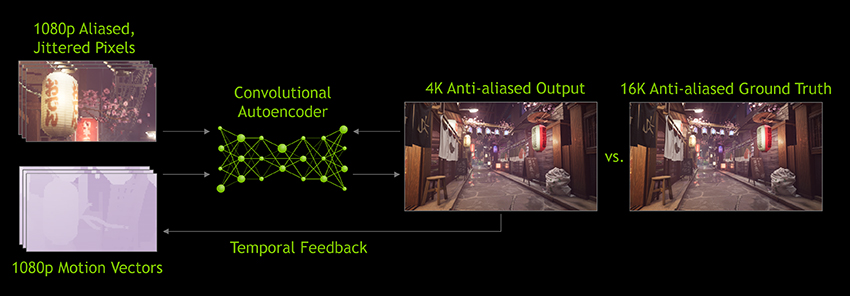 NVIDIA DLSS 2.0
NVIDIA DLSS 2.0
Deep Learning for Graphics: NVIDIA DLSS
Deep Learning for Graphics: NVIDIA DLSS

Deep Learning for Graphics: NeRF

- Mildenhall et al, ”NeRF: Representing Scenes as Neural Radiance Fields for View Synthesis”, ECCV 2020
Deep Learning for Scientific Applications
Deep Learning for Scientific Applications
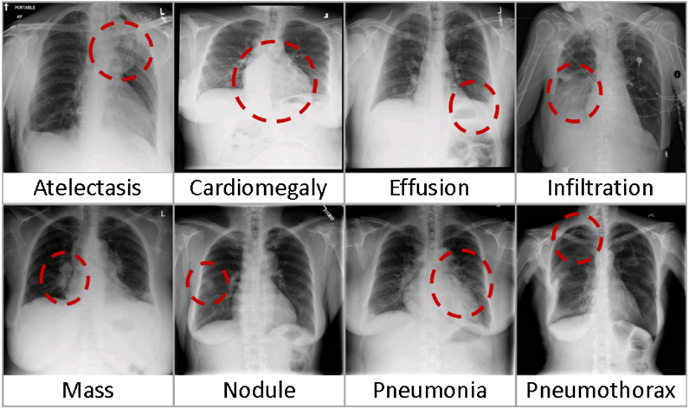



Deep Learning for Science: Protein Folding
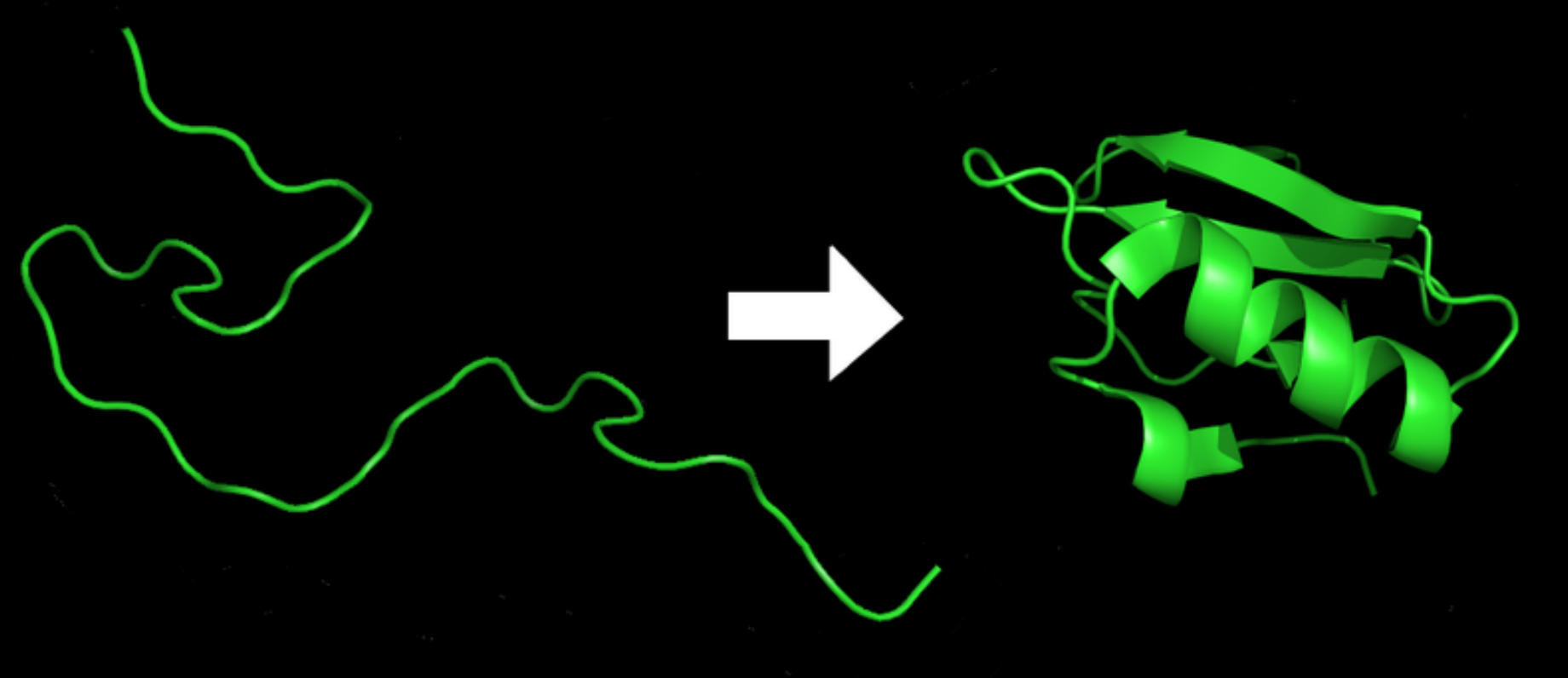
- Input: 1D sequence of amino acids
- Output: 3D protein structure
Deep Learning for Science: Protein Folding
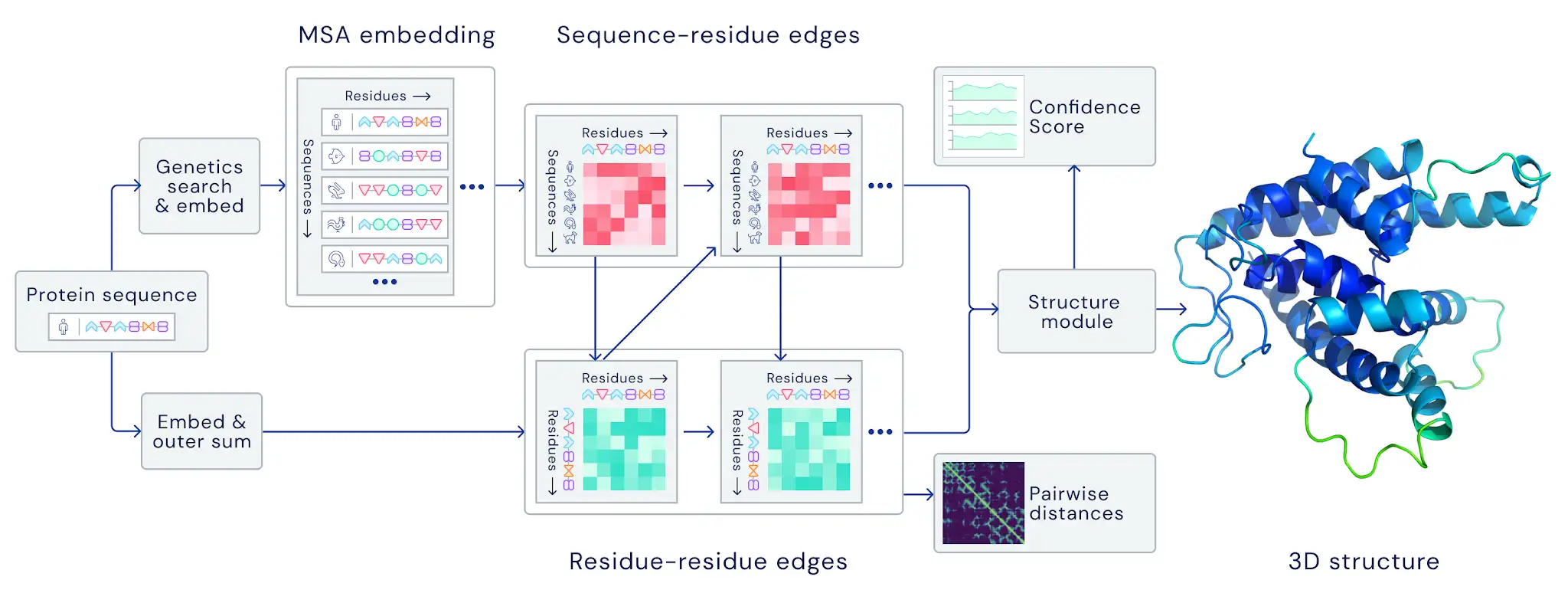
Deep Learning for Science: Protein Folding

Deep Learning for Mathematics
- Convert mathematical expressions into graphs, process them with graph neural networks.
- Applications: Theorem proving, symbolic integration

- Wang et al, "Premise selection for Theorem Proving by Deep Graph Embedding", NeurIPS 2017
- Kaliszyk et al, "Reinforcement Learning of Theorem Proving", NeurIPS 2018
- Wang et al, "Deep Learning for Symbolic Mathematics", Arxiv 2019
AutoML: Neural Architecture Search
Early DNN Architecture Development
- Primarily driven by skilled practitioners and elaborated design.
- a.k.a "Graduate Student Design"


Not scalable to the increasing demand for AI solutions.
Automating DNN Design





The Promise of NAS
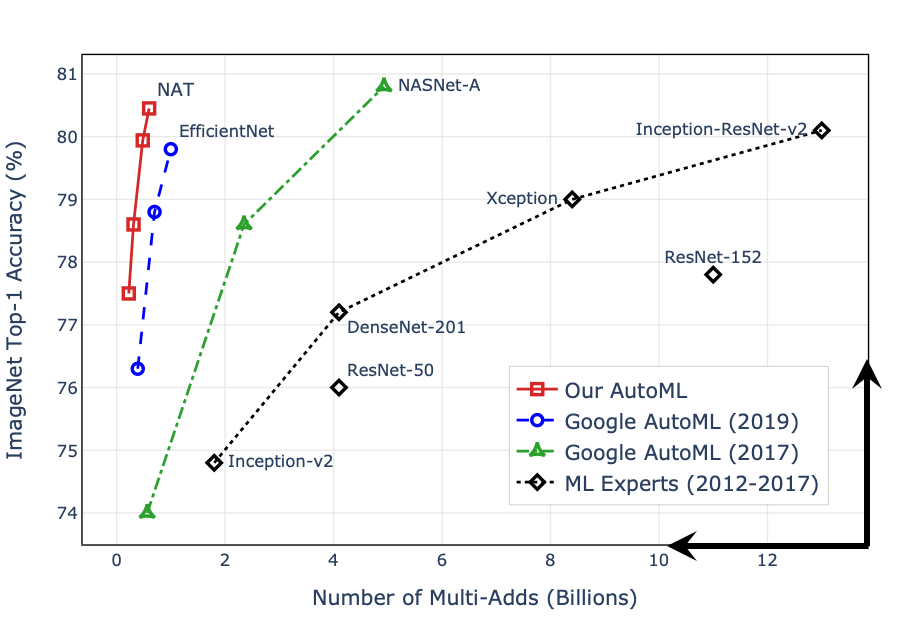
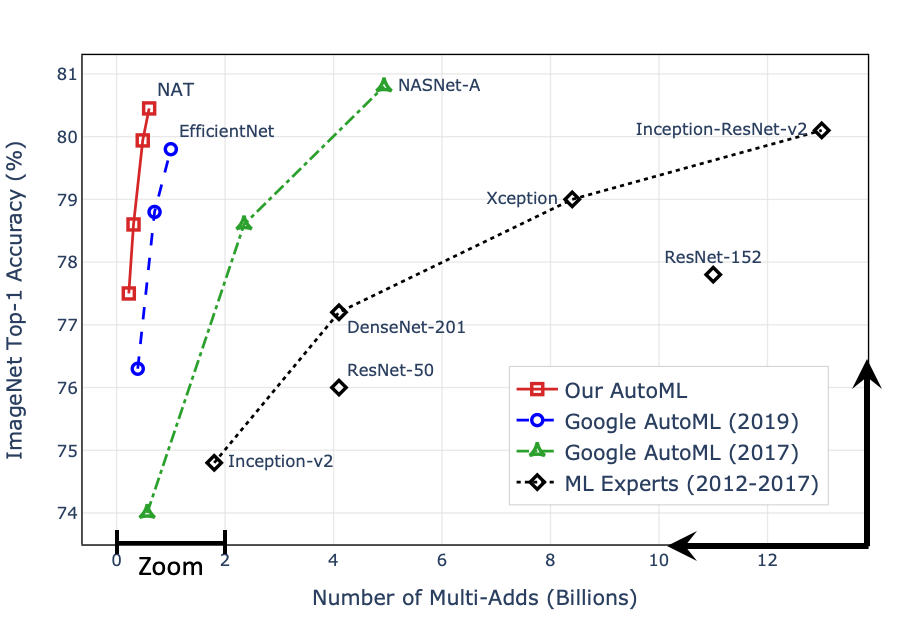
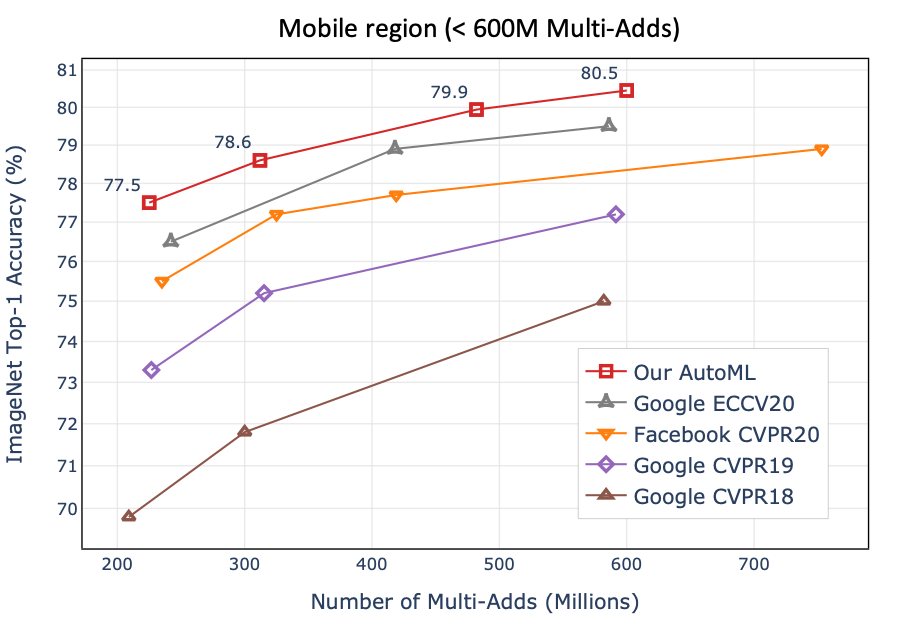
- New state-of-the-art 80.5% ImageNet Top-1 accuracy under mobile setting.
- Zhichao Lu et al "NSGANetV2:Evolutionary Multi-Objective Surrogate-Assisted Neural Architecture Search", ECCV 2020
- Zhichao Lu et al "Neural Architecture Transfer", Transactions on Pattern Analysis and Machine Inteliigence 2021
Problems with Deep Learning
Empirical Mystery: Good Subnetworks
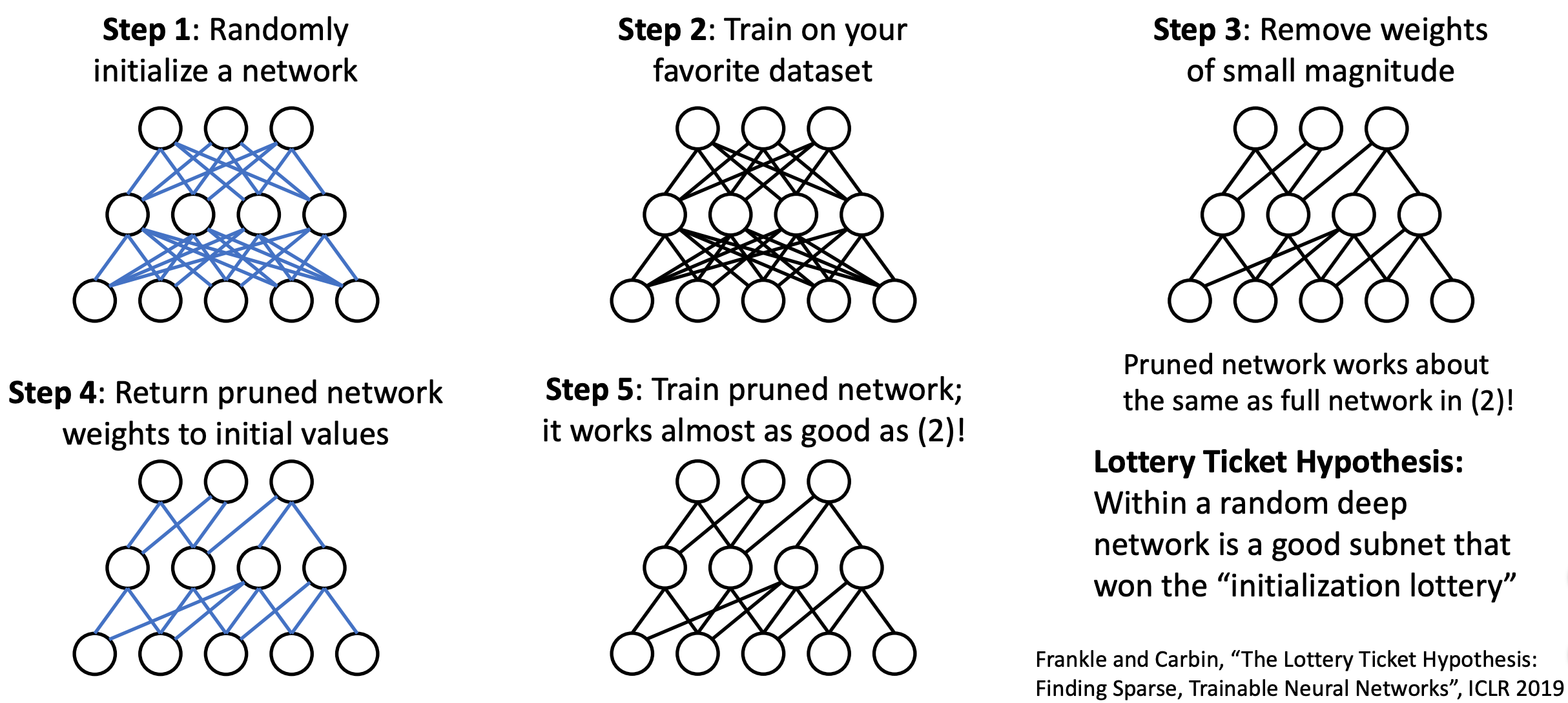
Empirical Mystery: Good Subnetworks
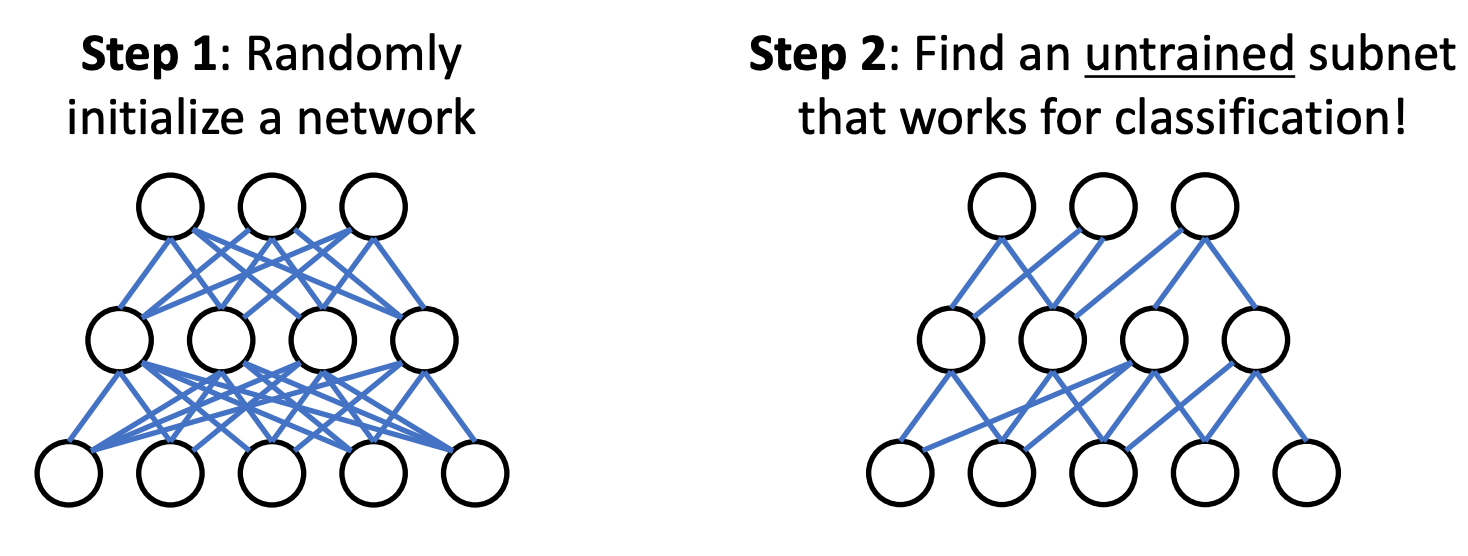
- We do not understand how to train and initialize deep networks, and what training actually does.
- Ramanujan et al "What's hidden in a randomly weighted neural network?," arxiv 2019
Empirical Mystery: Generalization
- What we expect from classical statistical learning theory:
- Why don't deep neural networks overfit?
- "Double Descent" for deep networks does not match theory.
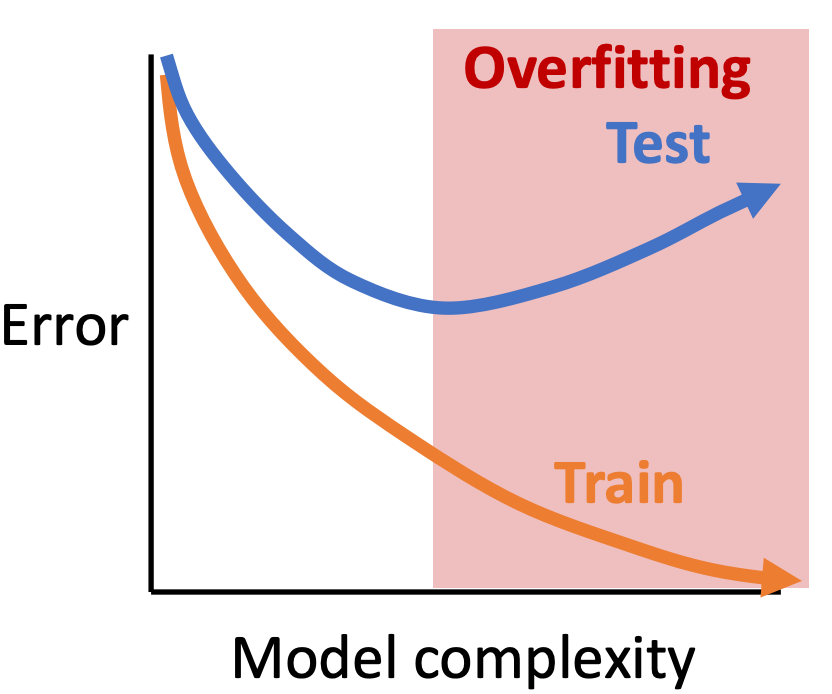
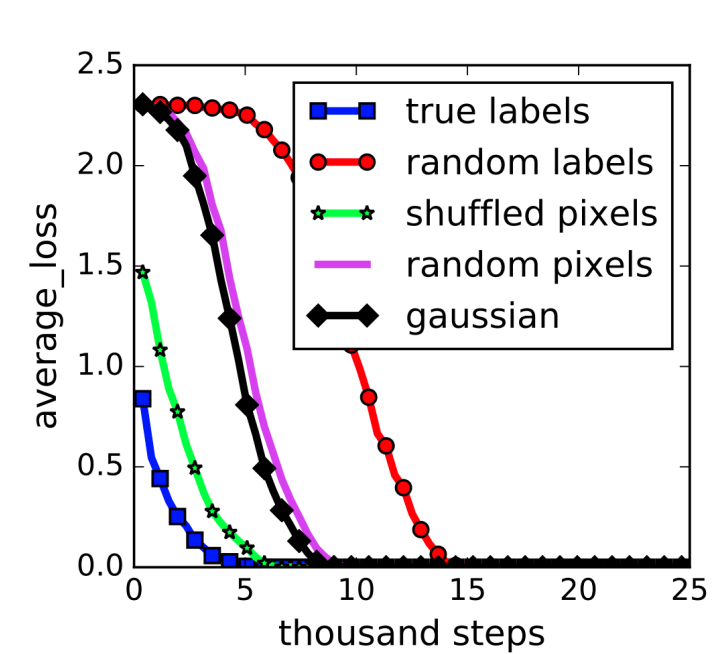
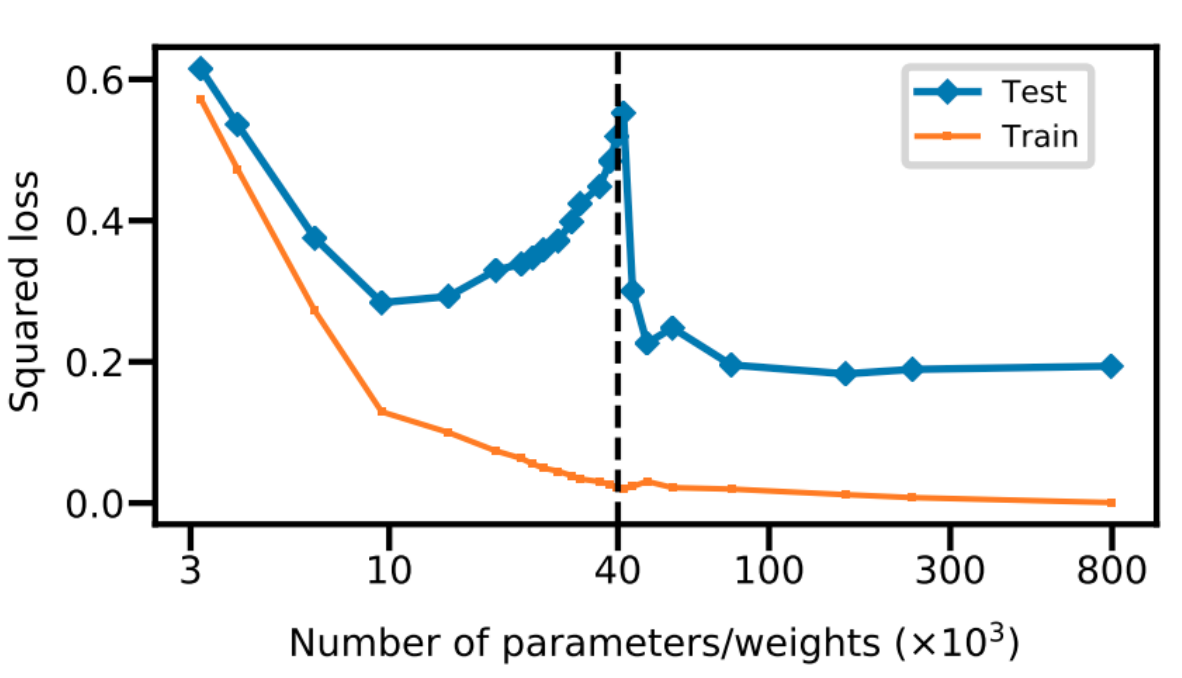
- Belkin et al "Reconciling modeern machine learning practice and the bias-variance trade-off," PNAS 2019
Deep Learning Does Not "Understand" the World
Language Models Lack Common Sense
- Input: I was born in 1950. In the year 2025 my age will be 35.
- Response from GPT-2: That was only a few years ago. Most things in life just continue to improve.
- Input: I see a black dog and a brown horse. The bigger animal's color is
- Response from GPT-2: black, and the smaller is brown.
- One of my parents is a doctor and the other is a professor. My father is a professor. My mother is
- Response from GPT-2: a social worker. They're super smart people.
"The Elephant in the Room"

- Rosenfeld et al "The Elephant in the Room," arxiv 2018
"The Elephant in the Room"

- Rosenfeld et al "The Elephant in the Room," arxiv 2018
Causality


- Wang and Boddeti, "Do learned representations respect causal relationships?," CVPR 2022
Deep Learning Future?
- New Deep Learning Models
- New Applications
- AutoML: Neural Architecture Search
- Models are biased
- Models leak sensitive private information
- Need new theory
- Understanding the World