Constraint Satisfaction - I


CSE 440: Introduction to Artificial Intelligence

Vishnu Boddeti


Content Credits: CMU AI, http://ai.berkeley.edu

What are Constraint Satisfaction Problems?

  • Special kind of search problems.
    • $N$ variables
    • Values from domain $D$
    • assignment satisfies constraints
  • States: partial assignment
  • Goal Test: satisfies all constraints
  • Successor Function: assign an unassigned variable

Today

  • Constraint Satisfaction
  • Reading
    • Today's Lecture: RN Chapter 6
    • Next Lecture: RN Chapter 6

What is Search For?

  • Given assumptions about the world: a single agent, deterministic actions, fully observed state, discrete state space
    • Planning: sequences of actions
      • The path to the goal is the important thing
      • Paths have various costs, depths
      • Heuristics give problem-specific guidance
    • Identification: assignments to variables
      • The goal itself is important, not the path
      • All paths at the same depth (for some formulations)
      • CSPs are a specialized class of identification problems

Constraint Satisfaction Problems

What are Constraint Satisfaction Problems?

  • Standard search problems:
    • State is a "black box": arbitrary data structure
    • Goal test can be any function over states
    • Successor function can also be anything
  • Constraint satisfaction problems (CSPs):
    • A special subset of search problems
    • State is defined by variables $\mathbf{X}_i$ with values from a domain $D$ (sometimes $D$ depends on $i$)
    • Goal test is a set of constraints specifying allowable combinations of values for subsets of variables
  • Allows useful general-purpose algorithms with more power than standard search algorithms

CSP Example

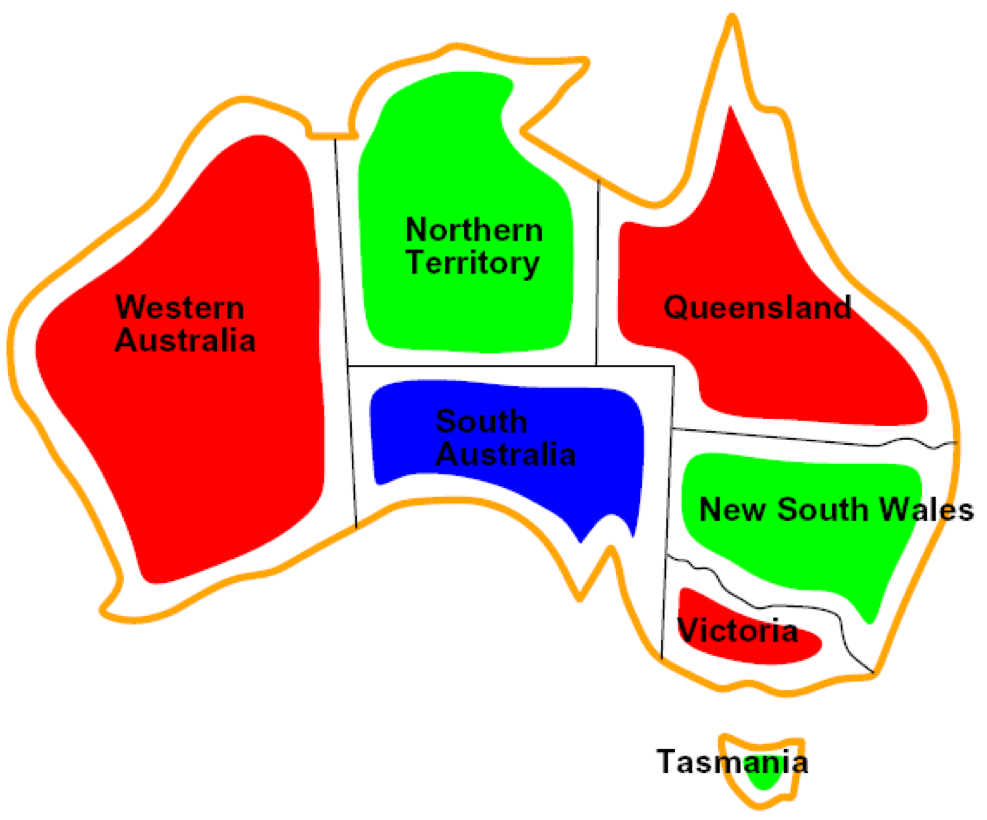
Example: Map Coloring

  • Variables: $WA$,$NT$,$Q$,$NSW$,$V$,$SA$,$T$
  • Domains: $D=\{red, green, blue\}$
  • Constraints: adjacent regions must have different colors
    • Implicit: $WA \neq NT$
    • Explicit: $(WA,NT) \in {(red, green),(red, blue),\dots}$
  • Solutions: Assignments that satisfy all constraints, e.g.:
    • {WA=red, NT=green, Q=red, NSW=green, V=red, SA=blue, T=green}

Constraint Graphs

  • Binary CSP: each constraint relates two variables
  • Constraint Graph: nodes are variables, arcs are constraints
  • General-purpose CSP algorithms use the graph structure to speed up search. E.g., Tasmania is an independent subproblem.

Example: N Queens

  • Formulation 1:
    • Variables: $X_{ij}$
    • Domains: $\{0,1\}$
    • Constraints:
$$ \begin{eqnarray} \forall \mbox{ } i,j,k && (X_{ij}, X_{ik}) \in {(0,0),(0,1),(1,0)}\nonumber \\ \forall \mbox{ } i,j,k && (X_{ij}, X_{kj}) \in {(0,0),(0,1),(1,0)}\nonumber \\ \forall \mbox{ } i,j,k && (X_{ij}, X_{i+k,j+k}) \in {(0,0),(0,1),(1,0)}\nonumber \\ \forall \mbox{ } i,j,k && (X_{ij}, X_{i+k,j-k}) \in {(0,0),(0,1),(1,0)}\nonumber \\ \sum_{ij}X_{ij}&=&N \nonumber \end{eqnarray} $$

Example: N Queens

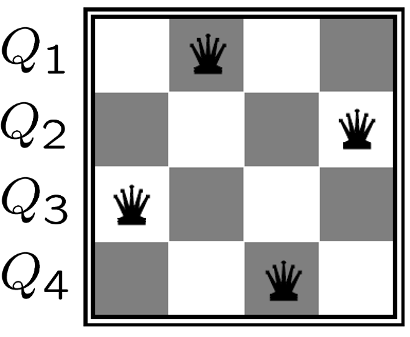
  • Formulation 2:
    • Variables: $Q_k$
    • Domains: ${1,2,3,\dots,N}$
    • Constraints:
      • Implicit: $\forall(i,j) \mbox{ non-threatening } (Q_i, Q_j)$
      • Explicit: $(Q_1, Q_2) \in \{(1,3),(1,4),\dots\}$

Example: The Waltz Algorithm

Example: The Waltz Algorithm
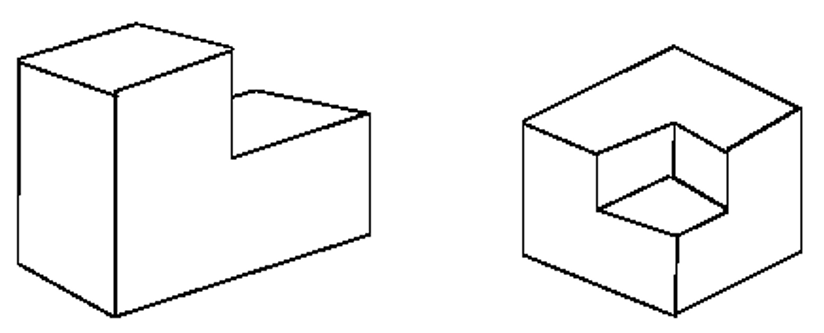
  • The Waltz algorithm is for interpreting line drawings of solid polyhedra as 3D objects
  • An early example of an AI computation posed as a CSP
  • Approach:
    • Each intersection is a variable
    • Adjacent intersections impose constraints on each other
    • Solutions are physically realizable 3D interpretations

Example: The Waltz Algorithm

Example: The Waltz Algorithm

Variety of CSPs

  • Discrete Variables
    • Finite domains
      • Size $d$ means $O\mathcal(d^n)$ complete assignments
      • E.g., Boolean CSPs, including Boolean satisfiability (NP-complete)
    • Infinite domains (integers, strings, etc.)
      • E.g., job scheduling, variables are start/end times for each job
      • Linear constraints solvable, nonlinear undecidable
  • Continuous variables
    • E.g., start/end times for Hubble Telescope observations
    • Linear constraints solvable in polynomial time by LP methods

Varieties of Constraints

  • Varieties of Constraints
    • Unary constraints involve a single variable (equivalent to reducing domains), e.g.: $SA \neq green$
    • Binary constraints involve pairs of variables, e.g.: $SA \neq WA$
    • Higher-order constraints involve 3 or more variables: e.g., cryptarithmetic column constraints
  • Preferences (soft constraints):
    • E.g., red is better than green
    • Often representable by a cost for each variable assignment
    • Leads to constrained optimization problems

Real-World CSPs

  • Scheduling problems: e.g., when can we all meet?
  • Timetabling problems: e.g., which class is offered when and where?
  • Assignment problems: e.g., who teaches what class
  • Hardware configuration
  • Transportation scheduling
  • Factory scheduling
  • Circuit layout
  • Fault diagnosis
  • $\cdots$

Solving CSPs

Standard Search Formulation

  • Standard search formulation of CSPs
  • States defined by the values assigned so far (partial assignments)
    • Initial state: the empty assignment, {}
    • Successor function: assign a value to an unassigned variable
    • Goal test: the current assignment is complete and satisfies all constraints
  • Start with straightforward search and then improve.

Search Methods

  • What would BFS do?
  • What would DFS do?
  • What problems does naïve search have?

Q & A

Image
XKCD