Convex Optimization
CSE 440: Introduction to Artificial Intelligence
Vishnu Boddeti
Content Credits: CMU AI, http://ai.berkeley.edu
Today
- Convexity
- Convex Optimization
Convex Optimization: Definition
- Convex Optimization Problem: \begin{equation} \begin{aligned} \min_{\mathbf{x}} & f(\mathbf{x}) \\ \nonumber \mbox{s.t. } & \mathbf{x} \in \mathcal{F} \end{aligned} \end{equation}
- A special class of optimization problem
- An optimization problem whose optimization objective $f$ is a convex function and feasible region $\mathcal{F}$ is a convex set.




Convex Combination
- A point between two points
- Given $\mathbf{x}, \mathbf{y} \in \mathbb{R}^n$, a convex combination of them is any point of the form $\mathbf{z}=\theta\mathbf{x}+(1-\theta)\mathbf{y}$ where $\theta \in [0,1]$.
- When $\theta \in (0,1)$, $\mathbf{z}$ is called a strict convex combination of $\mathbf{x}$, $\mathbf{y}$.
Convex Sets
- Conceptually: Any convex combination of two points in the set is also in the set
- Mathematically: A set $\mathcal{F}$ is convex if $\forall x,y\in \mathcal{F}, \forall \theta \in [0,1]$, $$\begin{equation} z = \theta x + (1-\theta) y \in \mathcal{F} \nonumber \end{equation}$$


Quiz: Convex Set
- Which of the following sets are convex?
- $\mathcal{F} = \mathbb{R}^n$
- $\mathcal{F} = \emptyset$
- $\mathcal{F} = \{\mathbf{x}_0\}, \mathbf{x}_0 \in \mathbb{R}^n$
- $\mathcal{F} = \mathcal{F}_1 \bigcap \mathcal{F}_2$, where $\mathcal{F}_1$ and $\mathcal{F}_2$ are convex sets.
- $\mathcal{F} = \mathcal{F}_1 \bigcup \mathcal{F}_2$, where $\mathcal{F}_1$ and $\mathcal{F}_2$ are convex sets.
- $\mathcal{F} = \mathbb{Z}^n$
Convex Function
- Value in the middle point is lower than average value
- Let $\mathcal{F}$ be a convex set. A function $f:\mathcal{F}\rightarrow\mathbb{R}$ is convex in $\mathcal{F}$ if $\forall x,y \in \mathcal{F}, \forall \theta \in [0,1]$, $$\begin{equation} \color{cyan}{f(\theta\mathbf{x} + (1-\theta)\mathbf{y})} \leq \color{orange}{\theta f(\mathbf{x}) + (1-\theta)f(\mathbf{y})} \nonumber \end{equation}$$
- If $\mathcal{F}=\mathbb{R}^n$, we simply say $f$ is convex.
How to determine if a functions is convex?
- Prove by definition
- Use properties of convex functions
- Sum of convex functions is convex $$\begin{equation} \mbox{If } f(\mathbf{x}) = \sum_{i} w_if_i(\mathbf{x}), w_i \geq 0, f_i(\mathbf{x}) \mbox{ convex, then } f(\mathbf{x}) \mbox{ is convex.} \nonumber \end{equation}$$
- Convexity is preserved under a linear transformation $$\begin{equation} \mbox{If } f(\mathbf{x}) = g(A\mathbf{x} + b), \mbox{ if } g(\mathbf{x}) \mbox{ is convex, then } f(\mathbf{x}) \mbox{ is convex.} \nonumber \end{equation}$$
- If $f$ is a twice differentiable function of one variable, $f$ is convex on an interval $[a,b]\subseteq \mathbb{R}$ iff (if and only if) its second derivative $f''(x) \geq 0$ in $[a,b]$
Convex Optimization: Definition
- If $f$ is a twice continuously differentiable function of $n$ variables, $f$ is convex on $\mathcal{F}$ iff its Hessian matrix of second partial derivatives is positive semidefinite on the interior of $\mathcal{F}$.
$$\begin{equation}
H(\mathbf{x}) = \begin{bmatrix}
\frac{\partial^2 f}{\partial x_1^2} & \frac{\partial^2 f}{\partial x_1x_2} & \dots & \frac{\partial^2 f}{\partial x_1x_n} \\
\frac{\partial^2 f}{\partial x_1x_2} & \frac{\partial^2 f}{\partial x_2^2} & \dots & \frac{\partial^2 f}{\partial x_2x_n} \\
\vdots & \vdots & \ddots & \vdots \\
\frac{\partial^2 f}{\partial x_1x_n} & \frac{\partial^2 f}{\partial x_2x_n} & \dots & \frac{\partial^2 f}{\partial x_n^2} \\
\end{bmatrix} \nonumber
\end{equation}$$
- $H$ is positive semidefinite in $S$ if $\forall \mathbf{x} \in S, \forall \mathbf{z}\in\mathbb{R}^n, \mathbf{z}^T H(\mathbf{x}) \mathbf{z} \geq 0$
- $H$ is positive semidefinite in $\mathbb{R}^n$ iff all eigenvalues of $H$ are non-negative.
- Alternatively, prove $\mathbf{z}^T H(\mathbf{x})\mathbf{z} = \sum_i g_i^2(x,z)$
Concavity and Convexity
- Concave function
- A function $f$ is concave if $-f$ is convex
- Let $\mathcal{F}$ be a convex set. A function $f:\mathcal{F}\rightarrow\mathbb{R}$ is concave in $\mathcal{F}$ if $\forall \mathbf{x},\mathbf{y}\in\mathcal{F}, \forall \theta\in[0,1]$, \[\color{cyan}{f(\theta\mathbf{x}+(1-\theta)\mathbf{y})} \geq \color{orange}{\theta f(\mathbf{x})+(1-\theta)f(\mathbf{y})}\]
- The following is a convex optimization problem if $f$ is a concave function and $\mathcal{F}$ is a convex set $$\begin{equation} \begin{aligned} \max_{\mathbf{x}} & f(\mathbf{x}) \\ \nonumber \mbox{s.t. } & \mathbf{x} \in \mathcal{F} \end{aligned} \end{equation}$$
Quiz 2: Convex Function
- Which of the following functions are convex?
- $f(x) = e^{ax}, a\in\mathbb{R}$
- $f(x) = \log x, x\in(0,+\infty)$
- $f(x) = \|\mathbf{x}\|_2=\sqrt{\sum_{i}^nx_i^2}$
- $f(\mathbf{x},\mathbf{y})=\mathbf{x}^T\mathbf{A}\mathbf{y}$, $\mathbf{A}\in\mathbb{R}^{m\times n}$, $\mathbf{x}\in\mathbb{R}^{m}$, $\mathbf{y}\in\mathbb{R}^{n}$
- $f(x)=x^3, x\in\mathbb{R}$
Convex Optimization: Local Optima=Global Optima
$$ \begin{equation} \begin{aligned} \min_{\mathbf{x}} & f(\mathbf{x}) \\ \nonumber \mbox{s.t. } & \mathbf{x} \in \mathcal{F} \end{aligned} \end{equation} $$- Given an optimization problem, a point $\mathbf{x}\in\mathbb{R}^n$ is globally optimal if $\mathbf{x}\in\mathcal{F}$ and $\forall \mathbf{y}\in\mathcal{F}$, $f(\mathbf{x})\leq f(\mathbf{y})$
- Given an optimization problem, a point $\mathbf{x}\in\mathbb{R}^n$ is locally optimal if $\mathbf{x}\in\mathcal{F}$ and $\exists R>0$ such that $\forall \mathbf{y}:\mathbf{y}\in\mathcal{F}$ and $\|\mathbf{x}-\mathbf{y}\|_2\leq R$, $f(\mathbf{x})\leq f(\mathbf{y})$
- Theorem 1: For a convex optimization problem, all locally optimal points are globally optimal
Convex Optimization: How to Solve?
- Recall discrete setting
- Local search
- Iteratively improving an assignment
- Continuous and differentiable setting
- Iteratively improving value of $\mathbf{x}$
- Based on gradient
Convex Optimization: How to Solve?
- For $f:\mathbb{R}^n\rightarrow\mathbb{R}$, gradient is the vector of partial derivatives
- A multi-variable generalization of the derivative
- Point in the direction of steepest increase in $f$
Gradient Descent


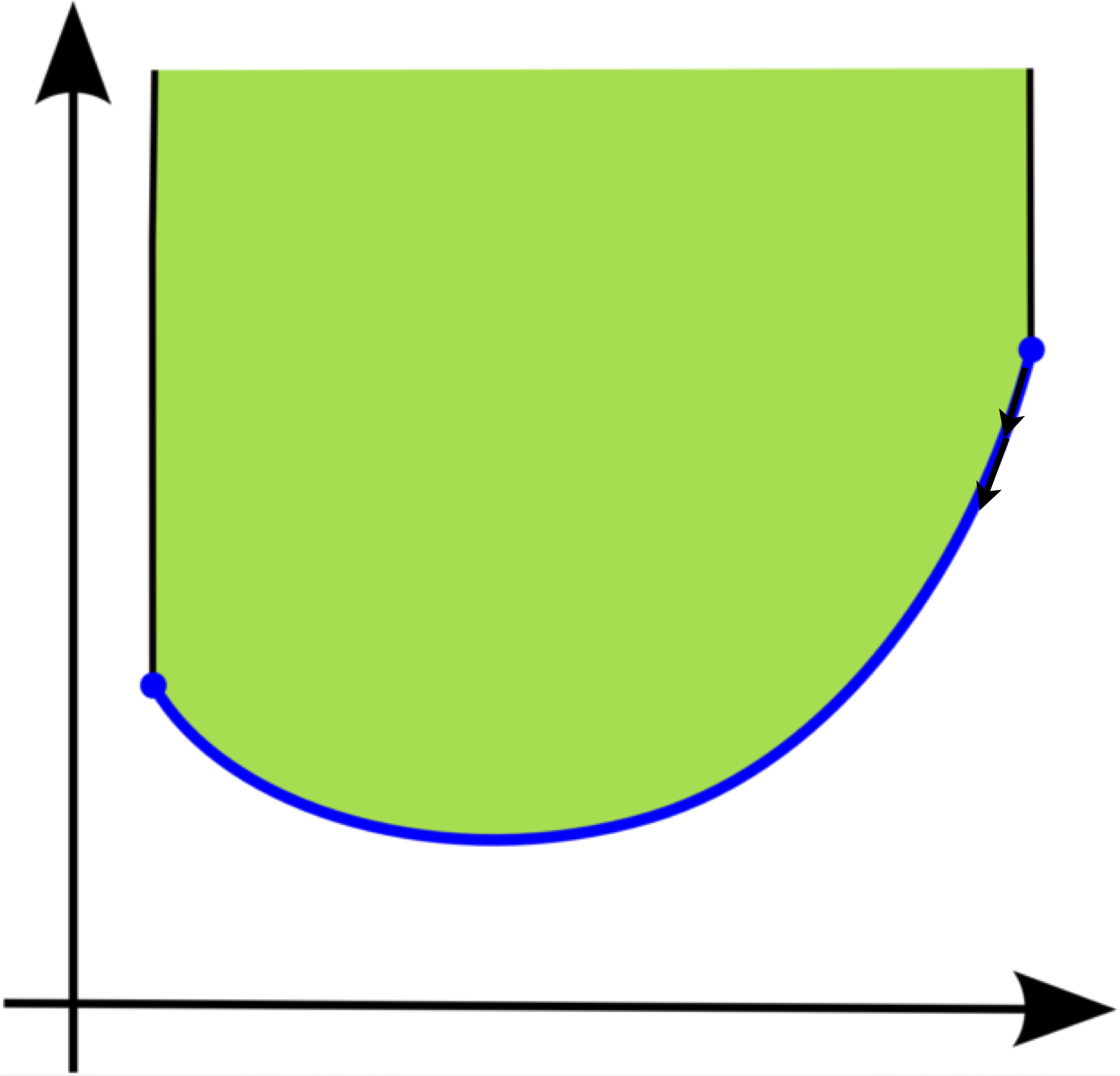
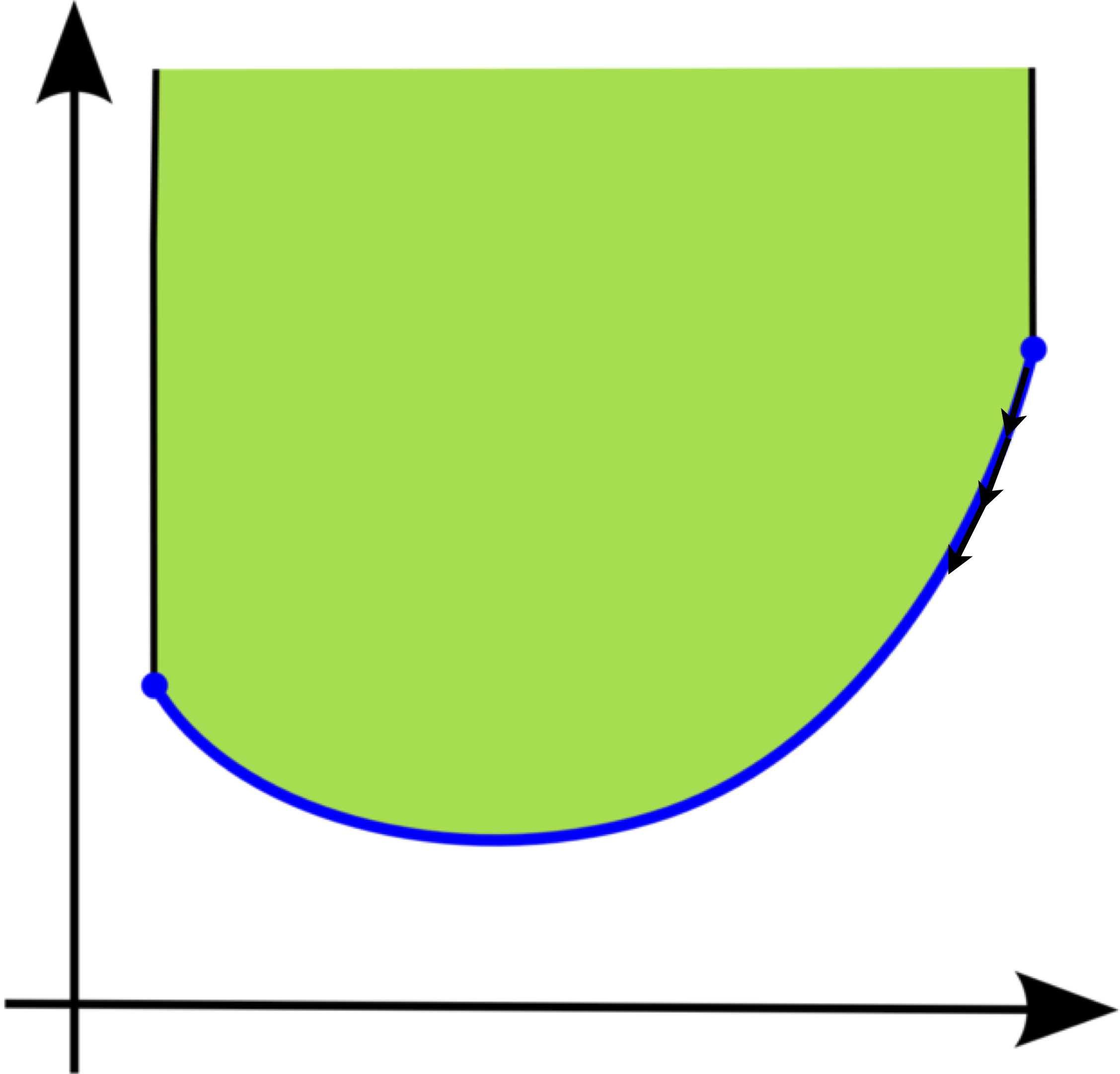
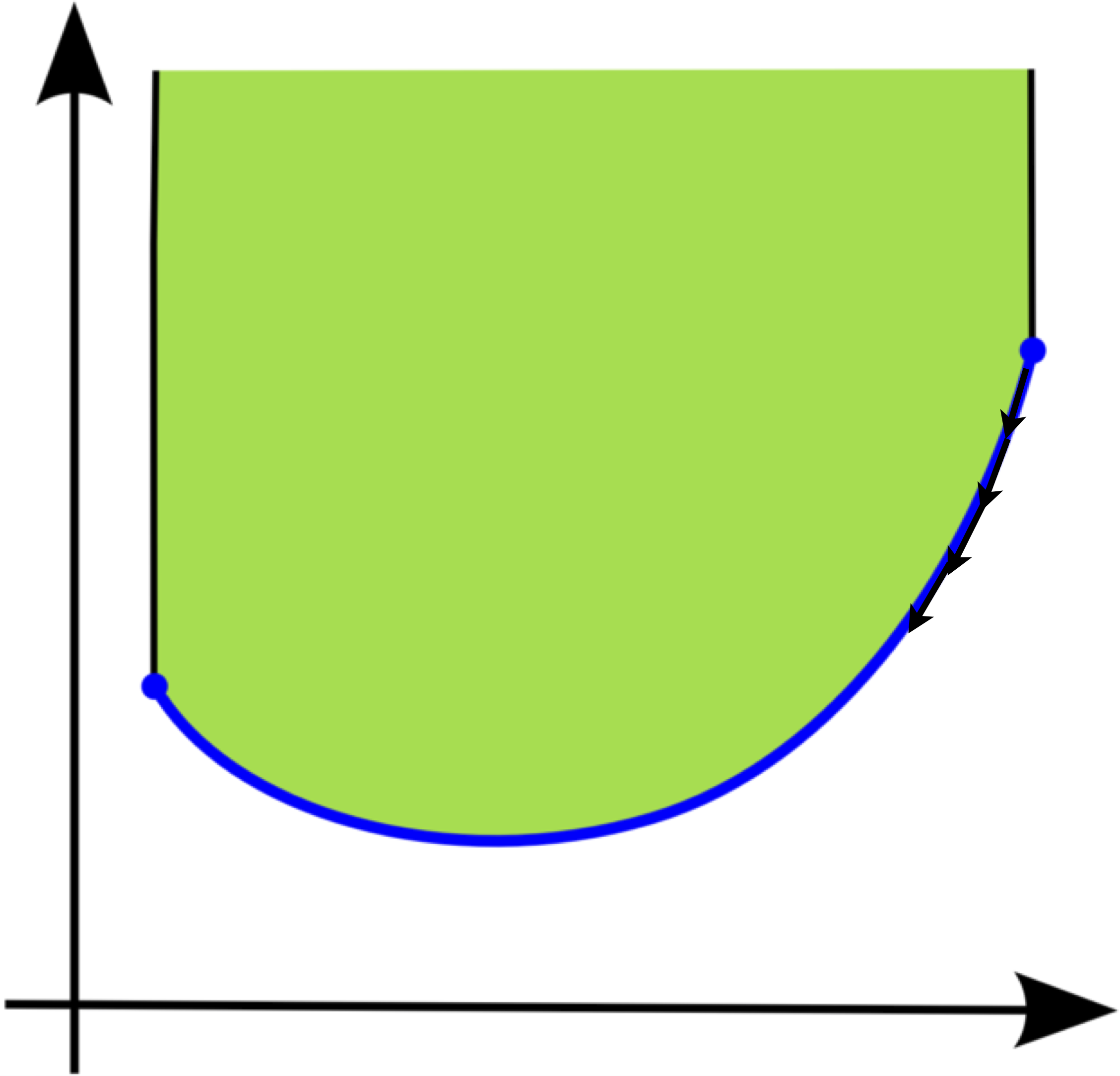

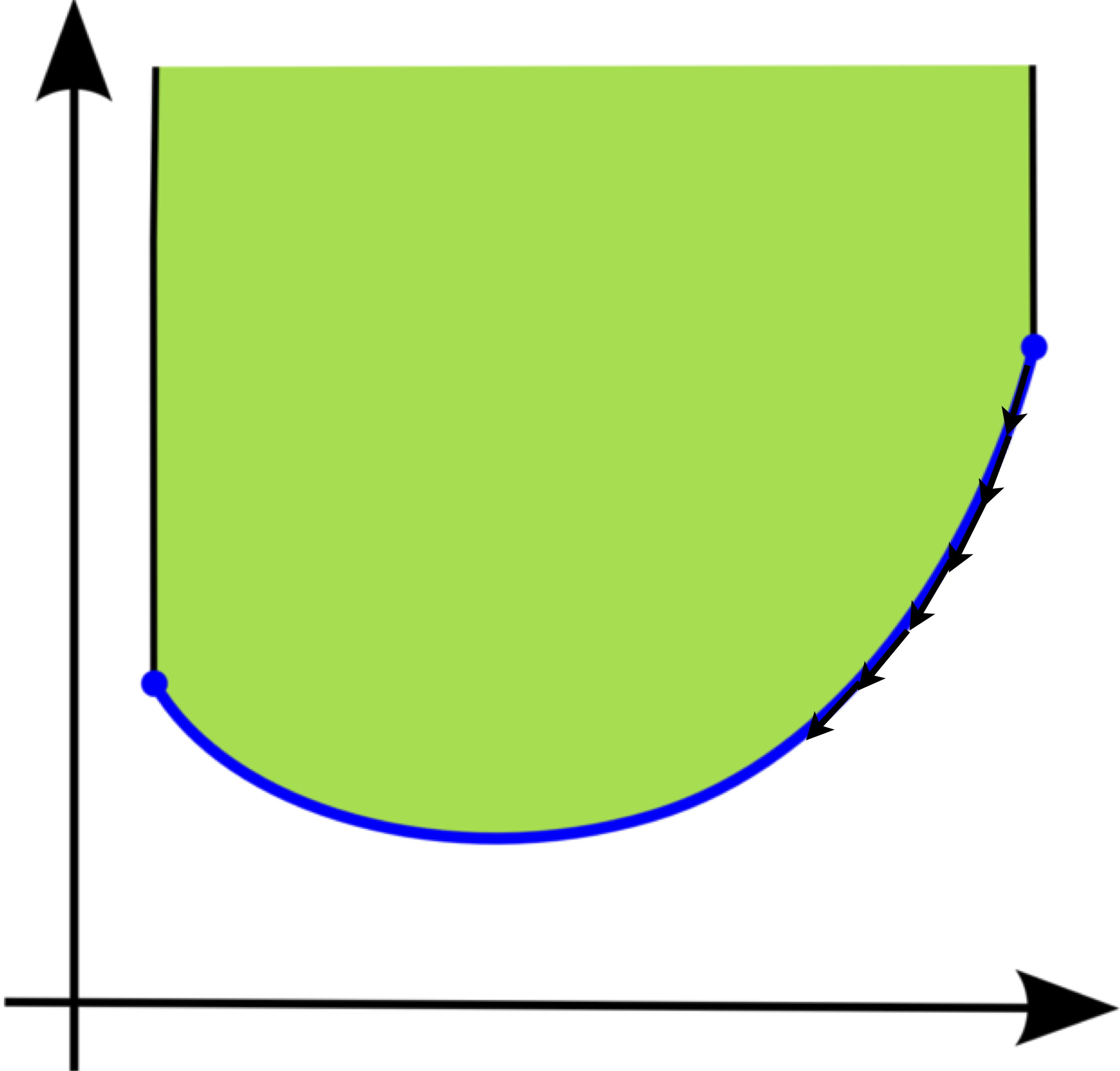
Convex Optimization: How to Solve?
- Gradient descent: iteratively update the value of $\mathbf{x}$
- A simple algorithm for unconstrained optimization $\min_{\mathbf{x}\in\mathbb{R}^n} f(\mathbf{x})$
- Variants
- How to choose $\mathbf{x}_0$, e.g., $\mathbf{x}_0=\mathbf{0}$
- How to choose and update step-size $\alpha$, e.g., trial and error, line-search methods etc.
- How to define "convergence", e.g., $\|\mathbf{x}^{i+1}-\mathbf{x}^i\| \leq \epsilon$

Projected Gradient Descent
- Iteratively update the value of $\mathbf{x}$ while ensuring $\mathbf{x}\in\mathcal{F}$
- $P_{\mathcal{F}}$ projects a point to the constraint set.
- Variant:
- How to choose $P_{\mathcal{F}}$, e.g., $P_{\mathcal{F}}=\underset{\mathbf{x'} \in \mathcal{F}}{\operatorname{arg min}}\|\mathbf{x}-\mathbf{x'}\|_2^2$

Convex Optimization: How to Solve?
- Unconstrained and differentiable
- Gradient descent
- Set derivative to be 0
- Closed form solution
- (Not covered) Newton's Method (if twice differentiable)
- Constrained and differentiable
- (Not covered) Projected gradient descent
- (Not covered) Interior Point Method
- (Not covered) Non-differentiable
- $\epsilon$-Subgradient Method
- Cutting Plane Method
Convex Optimization: Apply
- Model a problem as a convex optimization problem
- Define variable, feasible set, objective function
- Prove it is convex (convex function + convex set)
- Solve the convex optimization problem
- Build up the model
- Call a solver
- Examples: fmincon (MATLAB), cvxpy (Python), cvxopt (Python), cvx (MATLAB)
- Map the solution back to the original problem
Q & A