Bayesian Networks: Independence

CSE 440: Introduction to Artificial Intelligence

Vishnu Boddeti

Content Credits: CMU AI, http://ai.berkeley.edu

Today

D-Separation

Probability Recap

Conditional Probability: $P(x|y) = \frac{P(x,y)}{P(y)}$
Product Rule: $P(x,y)=P(x|y)P(y)$
Chain Rule: \begin{equation} \begin{aligned} P(x_1,\dots,x_n) &= P(x_1)P(x_2|x_1)P(x_3|x_2,x_1)\dots \nonumber \\ &= \prod_{i=1}^n P(x_i|x_1,\dots,x_{i-1}) \nonumber \end{aligned} \end{equation}
$X$,$Y$ independent if and only if: $\forall x,y \mbox{ : } P(x,y)=P(x)P(y)$
$X$ and $Y$ are conditionally independent given $Z$ if and only if: $\forall x,y,z \mbox{ : } P(x,y|z)=P(x|z)P(y|z)$

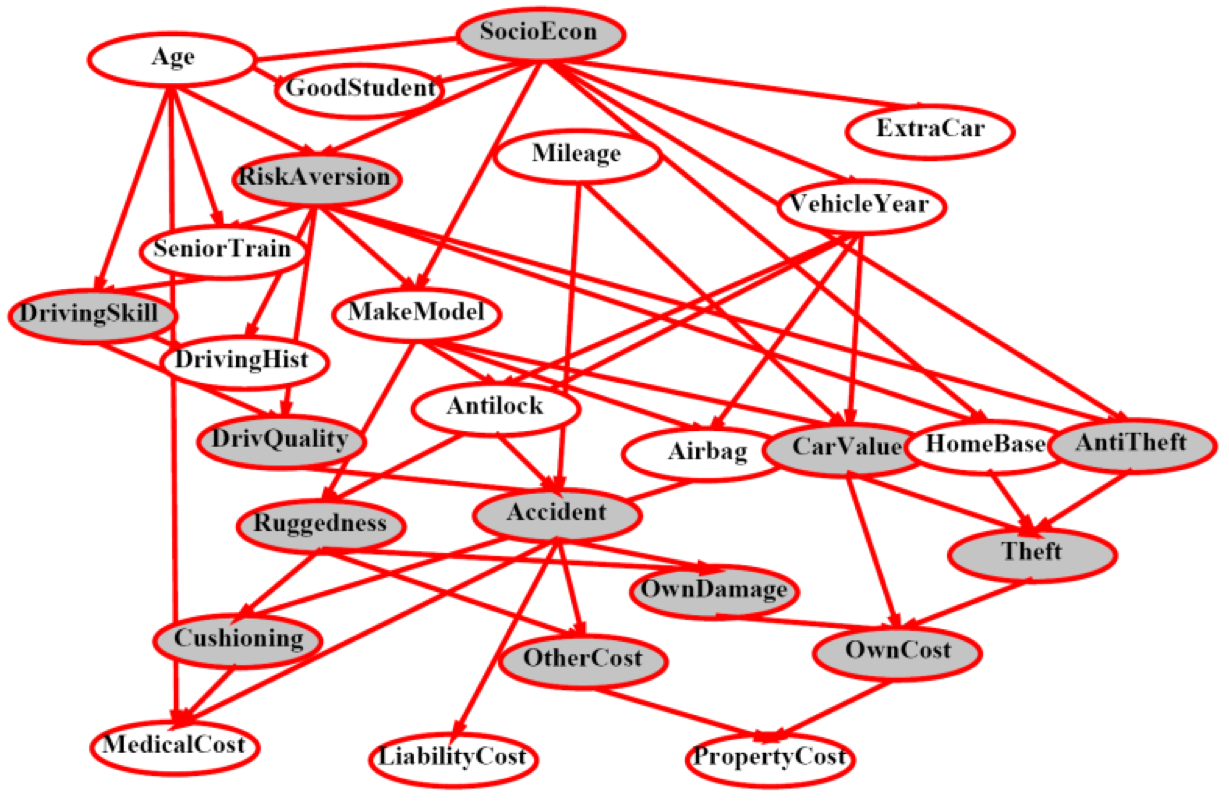
Bayes Net

A Bayes net is an efficient encoding of a probabilistic model of a domain.
Questions we can ask:

Inference: given a fixed BN, what is $P(X|e)$?
Representation: given a BN graph, what kinds of distributions can it encode?
Modeling: what BN is most appropriate for a given domain?

Bayes Net Semantics

A directed, acyclic graph, one node per random variable
A conditional probability table (CPT) for each node

A collection of distributions over X, one for each combination of parents values \[P(X|a_1,\dots,a_n)\]

Bayes nets implicitly encode joint distributions

As a product of local conditional distributions
To see what probability a BN gives to a full assignment, multiply all the relevant conditionals together: \[P(x_1,\dots,x_n) = \prod_{i=1}^n P(x_i|parents(x_i))\]

Example: Alarm Network

\begin{equation} \begin{aligned} P(+b,-e,+a,-j,+m) &= P(+b)P(-e)P(+a|+b,-e)P(-j|+a)P(+m|+a) \nonumber \\ &= 0.001\times 0.998 \times 0.94 \times 0.1 \times 0.7 \nonumber \end{aligned} \end{equation}

Size of a Bayes Net

How big is a joint distribution over $N$ Boolean variables?

\[2^N\]

How big is an $N$-node net if nodes have up to $k$ parents?

\[\mathcal{O}(N * 2^{k+1})\]

Both give you the power to calculate
BNs: Huge space savings
Also easier to elicit local CPTs
Also faster to answer queries (coming)

Bayes Net

Representation
Conditional Independences
Probabilistic Inference
Learning Bayes Nets from Data

Independence Conditions

Conditional Independence

X and Y are independent if: \[\forall x,y \mbox{ : } P(x,y)=P(x)P(y) \Rightarrow X \perp \!\!\! \perp Y\]
X and Y are conditionally independent given Z \[\forall x,y,z \mbox{ } P(x,y|z)=P(x|z)P(y|z) \Rightarrow X \perp \!\!\! \perp Y | Z\]
(Conditional) independence is a property of a distribution
Example: $Alarm \perp \!\!\! \perp Fire | Smoke$

Bayes Nets: Assumptions

Given the graph, assumptions we are required to make in order to define the Bayes net:
Beyond above "chain rule $\rightarrow$ Bayes net" conditional independence assumptions

Often additional conditional independences
They can be read off the graph

Important for modeling: understand assumptions made when choosing a Bayes net graph

Example

Conditional independence assumptions directly from simplifications in chain rule:

Additional implied conditional independence assumptions?

Independence in a BN

Important question about a BN:

Are two nodes independent given certain evidence?
If yes, can prove using algebra (tedious in general)
If no, can prove with a counter example
Example:
Question: are $X$ and $Z$ necessarily independent?

Answer: no. Example: low pressure causes rain, which causes traffic.
$X$ can influence $Z$, $Z$ can influence $X$ (via $Y$)
Addendum: they could be independent: how?

D-Separation

D-separation: Outline

Study independence properties for triples

Analyze complex cases in terms of member triples

D-separation: a condition / algorithm for answering such queries

Causal Chains

This configuration is a "causal chain"

Guaranteed $X$ independent of $Z$?

Set CPTs for which $X$ is not independent of $Z$. Sufficient to show this independence is not guaranteed.
Example:

Low pressure causes rain causes traffic, high pressure causes no rain causes no traffic
In numbers: \[P(+y|+x) = 1,P(-y|-x) = 1\] \[P(+z|+y)=1,P(-z|-y)=1\]

Causal Chains

This configuration is a "causal chain"

Guaranteed $X$ independent of $Z$ given $Y$?

\begin{equation} \begin{aligned} P(z|x,y) &= \frac{P(x,y,z)}{P(x,y)} \nonumber \\ &= \frac{P(x)P(y|x)P(z|y)}{P(x)P(y|x)} \nonumber \\ &= P(z|y) \nonumber \end{aligned} \end{equation}

Evidence along the chain "blocks" the influence

Common Cause

This configuration is a "common cause"

$Y$: project due
$X$: forums busy
$Z$: lab full

Guaranteed $X$ independent of $Z$?

One example set of CPTs for which $X$ is not independent of $Z$ is sufficient to show this independence is not guaranteed.
Example:

Project due causes both forums busy and lab full
In numbers: \[P(+x|+y)=1,P(-x|-y)=1\] \[P(+z|+y)=1,P(-z|-y)=1\]

Common Cause

This configuration is a "common cause"

$Y$: project due
$X$: forums busy
$Z$: lab full

Guaranteed $X$ and $Z$ independent given $Y$?

\begin{equation} \begin{aligned} P(z|x,y) &= \frac{P(x,y,z)}{P(x,y)} \nonumber \\ &= \frac{P(y)P(x|y)P(z|y)}{P(y)P(x|y)} \nonumber \\ &= P(z|y) \nonumber \end{aligned} \end{equation}

Observing the cause blocks influence between effects

Common Effect

Last configuration: two causes of one effect (v-structures)

$X$: raining
$Y$: ballgame
$Z$: traffic

Are $X$ and $Y$ independent?

Yes the ballgame and the rain cause traffic, but they are not correlated
Still need to prove they must be (try it)

Are $X$ and $Y$ independent given $Z$?

No seeing traffic puts the rain and the ballgame in competition as explanation

This is backwards from the other cases

Observing an effect activates influence between possible causes.

The General Case

General question: in a given BN, are two variables independent (given evidence)?

Solution: analyze the graph

Any complex example can be broken into repetitions of the three canonical cases

Reachability

Recipe: shade evidence nodes, look for paths in the resulting graph
Attempt 1: if two nodes are connected by an undirected path not blocked by a shaded node, they are reachable.
Almost works, but not quite

Where does it break?
Answer: the v-structure at T does not count as a link in a path unless "active"

Active/Inactive Paths

Question: Are $X$ and $Y$ conditionally independent given evidence variables ${Z}$?

Yes, if $X$ and $Y$ "d-separated" by $Z$
Consider all (undirected) paths from $X$ to $Y$
No active paths = independence !!

A path is active if each triple is active:

Causal chain $A \rightarrow B \rightarrow C$ where $B$ is unobserved (either direction)
Common cause $A \leftarrow B \rightarrow C$ where $B$ is unobserved
Common effect (aka v-structure): $A \rightarrow B \leftarrow C$ where B or one of its descendents is observed

All it takes to block a path is a single inactive segment

Active Triples

Inactive Triples

D-Separation

Query: $X_i \perp \!\!\! \perp X_j | \{X_{k_1},\dots,X_{k_n}\}$
Check all (undirected) paths between $X_i$ and $X_j$

If one or more active, then independence not guaranteed \[X_i \not \perp \!\!\! \perp X_j | \{X_{k_1},\dots,X_{k_n}\}\]
Otherwise (i.e. if all paths are inactive), then independence is guaranteed \[X_i \perp \!\!\! \perp X_j | \{X_{k_1},\dots,X_{k_n}\}\]

Structure Implications

Given a Bayes net structure, can run d-separation algorithm to build a complete list of conditional independences that are necessarily true of the form
This list determines the set of probability distributions that can be represented

Computing All Independences

Topology Limits Distributions

Given some graph topology $G$, only certain joint distributions can be encoded
The graph structure guarantees certain (conditional) independences
There might be more independence
Adding arcs increases the set of distributions, but has several costs
Full conditioning can encode any distribution

Bayes Nets Representation Summary

Bayes nets compactly encode joint distributions

Guaranteed independencies of distributions can be deduced from BN graph structure

D-separation gives precise conditional independence guarantees from graph alone

A Bayes net joint distribution may have further (conditional) independence that is not detectable until you inspect its specific distribution

Q & A