Feed Forward Networks: Introduction
CSE 849: Deep Learning
Vishnu Boddeti
Today
- Artificial Neuron
- Activation Functions
- Capacity of Neural Networks
- Biological Motivation
Simplest Neural Network
Artificial Neuron
- Neuron pre-activation (or input activation)
- $a(\mathbf{x}) = b + \sum_i w_ix_i = b + \mathbf{w}^T\mathbf{x}$
- Neuron (output) activation
- $h(\mathbf{x}) = g(a(\mathbf{x})) = g\left(b+\sum_iw_ix_i\right)$
- $\mathbf{w}$ are the connection weights
- $b$ is the neuron bias
- $g(\cdot)$ is called activation function

Artificial Neuron
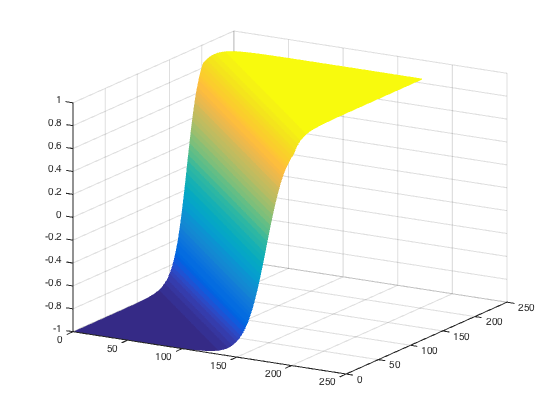
- range determined by $g(\cdot)$
- bias $b$ only changes the position of the riff
Linear Activation

- Performs no input squashing
- Quite a boring function...
Sigmoid Activation

- Squashes the neuron's pre-activation between 0 and 1
- Always positive
- Bounded
- Strictly increasing
Tanh Activation

- Squashes the neuron's pre-activation between -1 and 1
- Can be positive or negative
- Bounded
- Strictly increasing
Rectified Linear Unit Activation

- Bounded below by 0 (always non-negative)
- Not upper bounded
- Strictly increasing
- Tends to yeild neurons with sparse activities
Capcity of Neural Networks
Single Neuron
- Could do binary classification:
- with sigmoid, can interpret neuron as estimating $p(y=1|\mathbf{x})$
- also known as logistic regression classifier
- if greater than 0.5, predict class 1
- otherwise, predict class 0
- similar idea can be used with Tanh


Capacity of a Single Neuron
- Can solve linearly seperable problems






Capacity of a Single Neuron
- Cannot solve non-linearly separable problems....


- ...unless the input is transformed in a better representation
Neural Network with Hidden Layer
- Hidden layer pre-activation: $\mathbf{a}(\mathbf{x}) = \mathbf{b}_1 + \mathbf{W}_1\mathbf{x}$ $\left(a(\mathbf{x})^i = \mathbf{b}^i_1 + \sum_{j}W^{i,j}_1x^j\right)$
- Hidden layer activation: $\mathbf{h}(\mathbf{x}) = \mathbf{g}(\mathbf{a}(\mathbf{x}))$
- Output layer activation: $f(\mathbf{x}) = o(b_2 + \mathbf{w}_2^T\mathbf{h}(\mathbf{x}))$

Softmax Activation Function
- For multi-class classification:
- we need multiple outputs (1 output per class)
- we would like to estimate the conditional probability $p(y=c|\mathbf{x})$
- Softmax activation function at the output:
- strictly positive
- sums to one
- Predicted class: one with highest estimated probability
Multi-Layer Neural Network
- Could have $L$ hidden layers:
- layer pre-activation for $k>0$ ($\mathbf{h}^{(0)}(\mathbf{x})=\mathbf{x}$) $\mathbf{a}^{(k)}(\mathbf{x}) = \mathbf{b}^{(k)} + \mathbf{W}^{(k)}\mathbf{h}^{(k-1)}(\mathbf{x})$
- hidden layer activation ($k$ from 1 to $L$): $\mathbf{h}^{(k)}(\mathbf{x}) = \mathbf{g}(\mathbf{a}^{(k)}(\mathbf{x}))$
- output layer activation ($k=L+1$): $\mathbf{h}^{(L+1)}(\mathbf{x}) = \mathbf{o}(\mathbf{a}^{(L+1)}(\mathbf{x})) = f(\mathbf{x})$

Capacity of Single Hidden Layer Neural Network



Universal Approximation
- Universal approximation theorem (Hornik, 1991):
- "a single hidden layer neural network with a linear output unit can approximate any continuous function arbitrarily well, given enough hidden units"
- The result applies for sigmoid, tanh and many other hidden layer activation functions.
- This is a good result, but it doesn't mean there is a learning algorithm that can find the necessary parameter values.
- Many other function classes also known to be universal approximators.
Biological Inspiration
Biological and Artificial Neurons
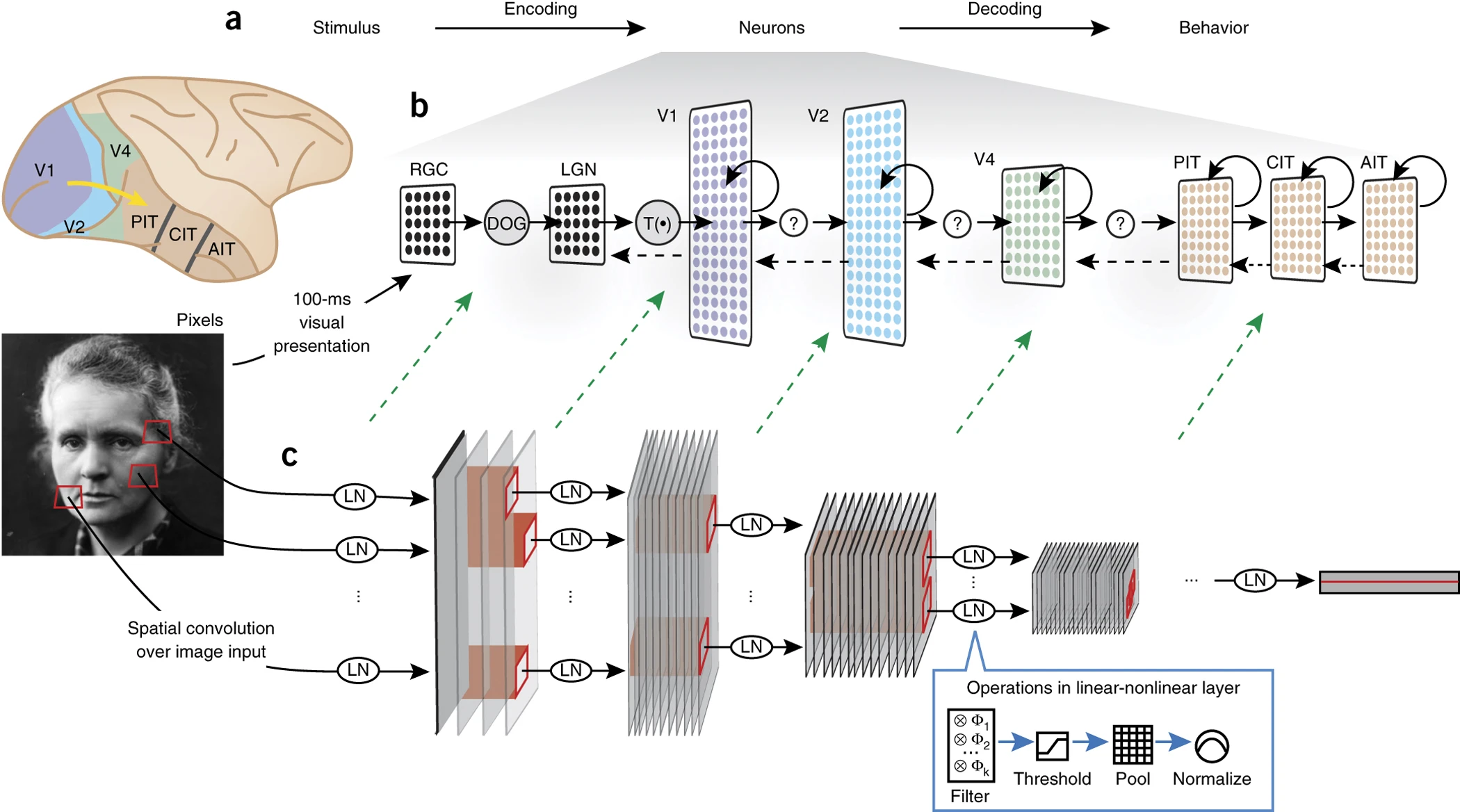
Biological and Artificial Neurons
Transistors and Biological Neurons
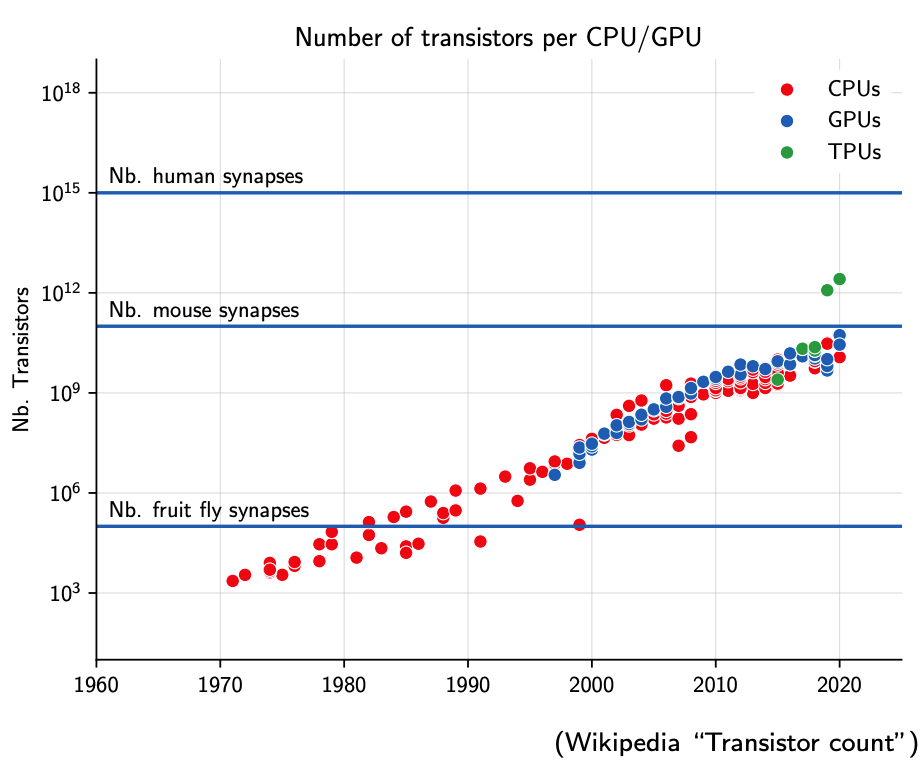
Image Credit: Francois Fleuret
Q & A