State Space Models
CSE 849: Deep Learning
Vishnu Boddeti
Today
- Attention Recap
- State Space Models
- S4 and Friends
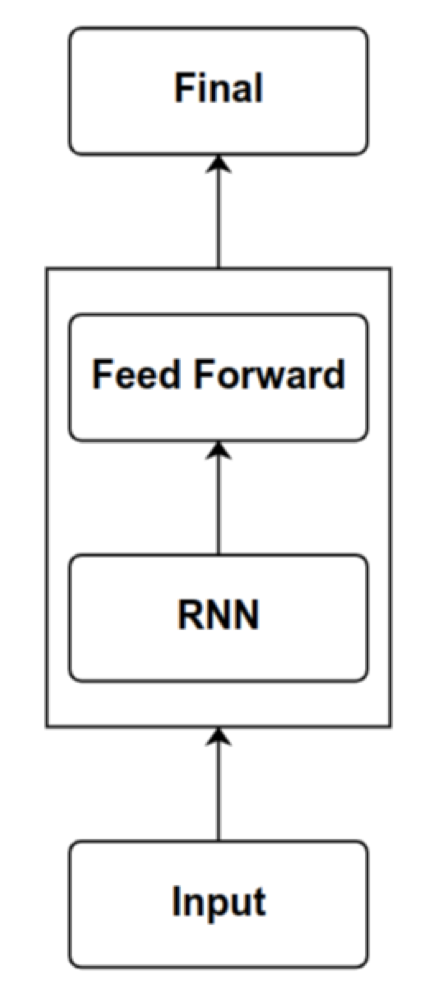
Transformers for Sequence Modeling
- Repeated Components
- Feed Forward
- Attention
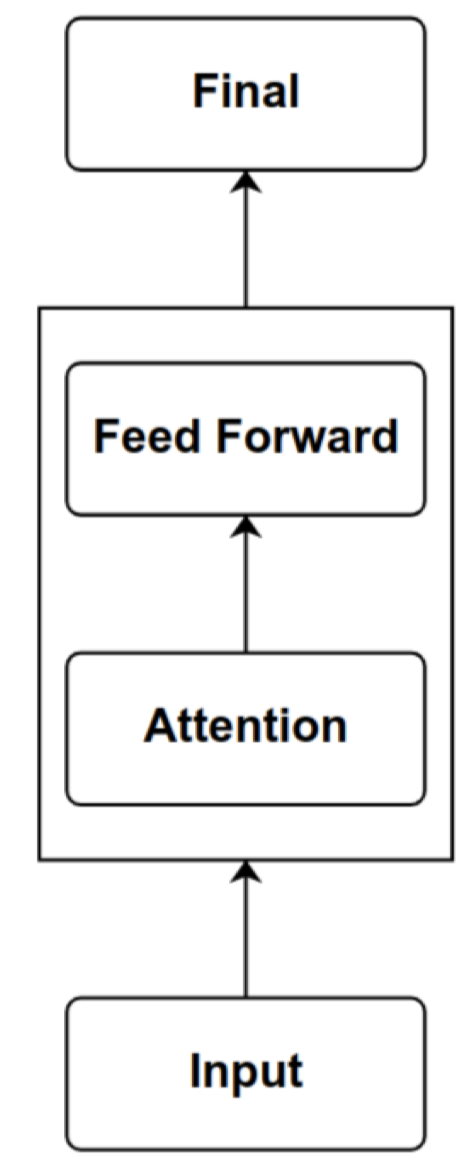
Feed Forward Layers
- Acts on each position independently.
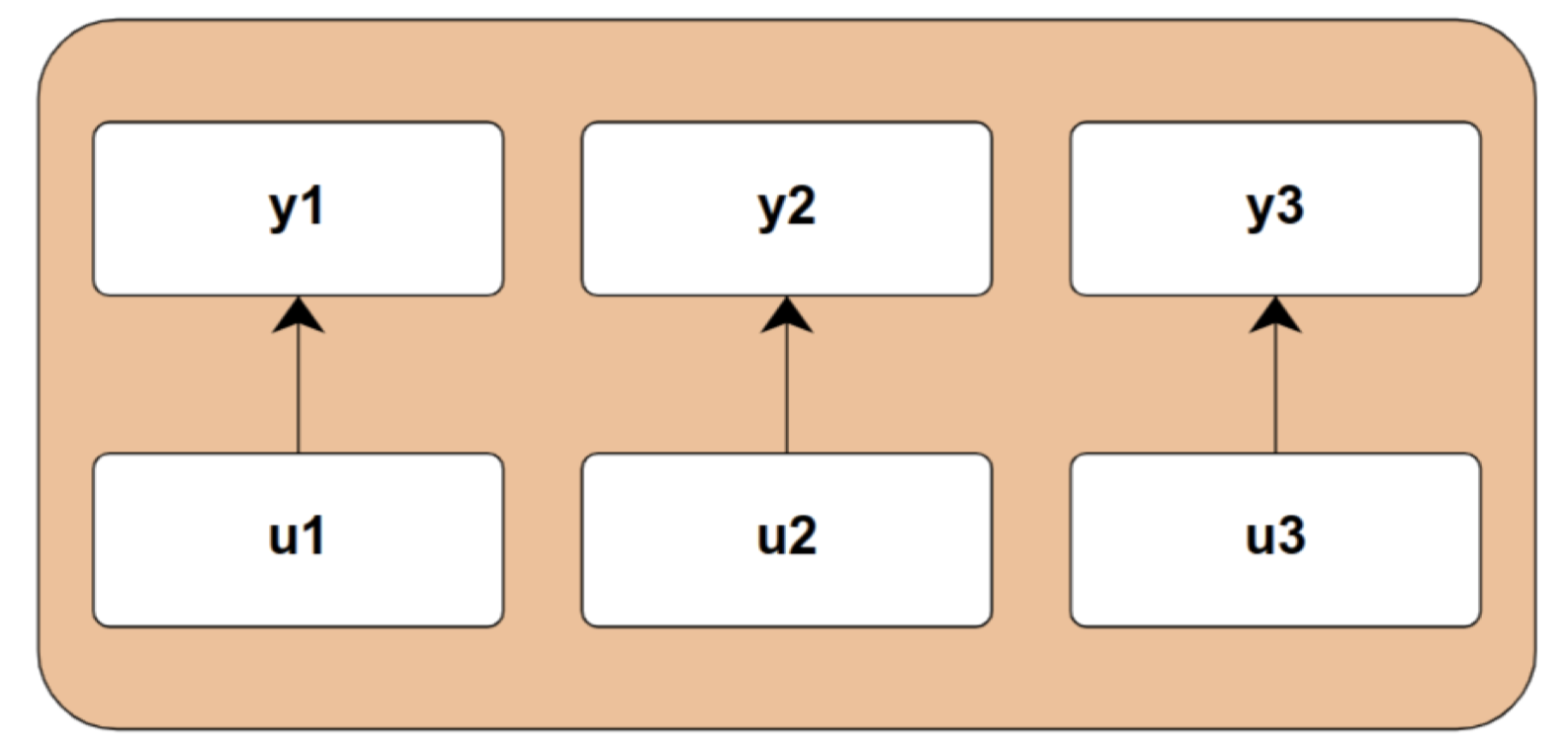
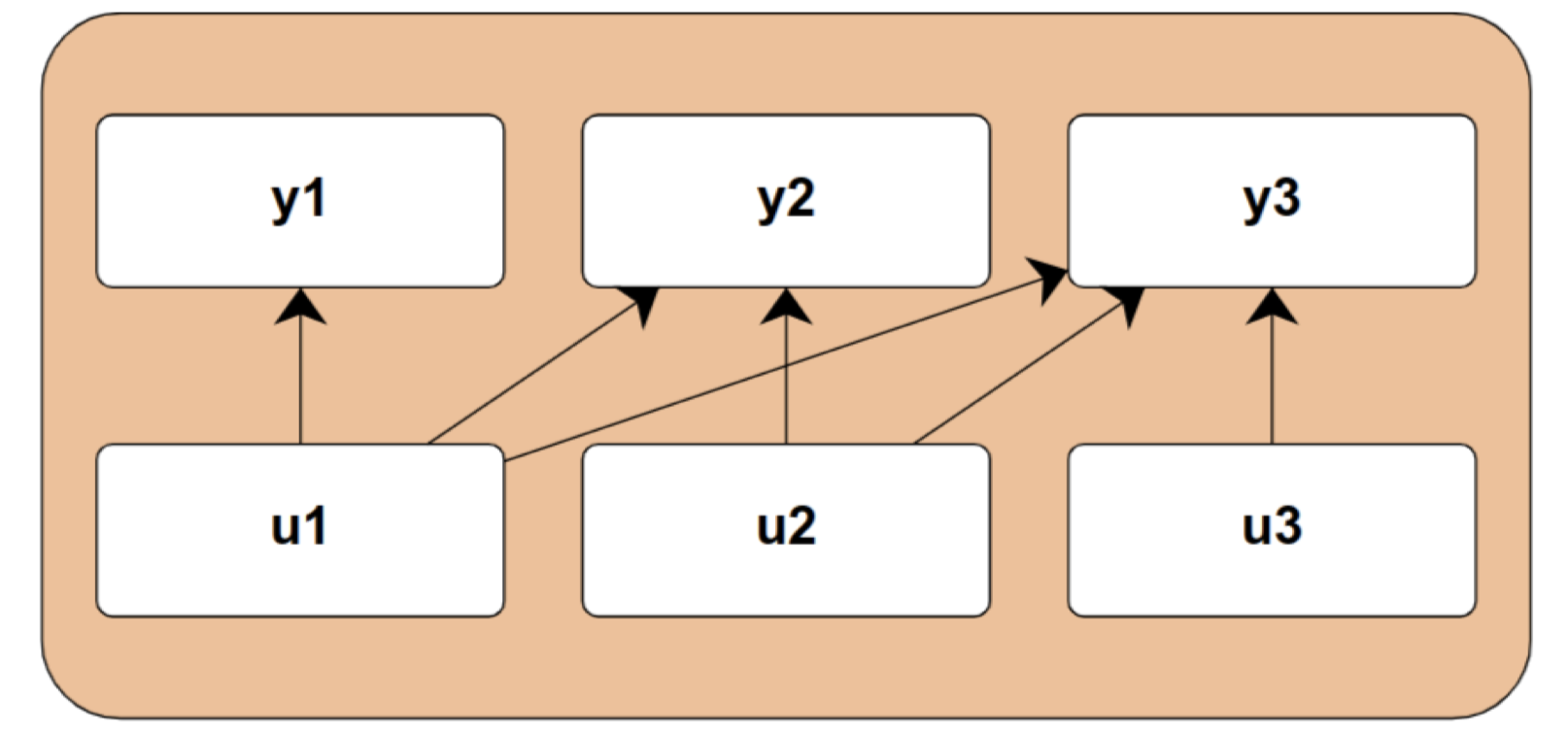
Attention
- Fully connected interactions.
Task: Language Generation
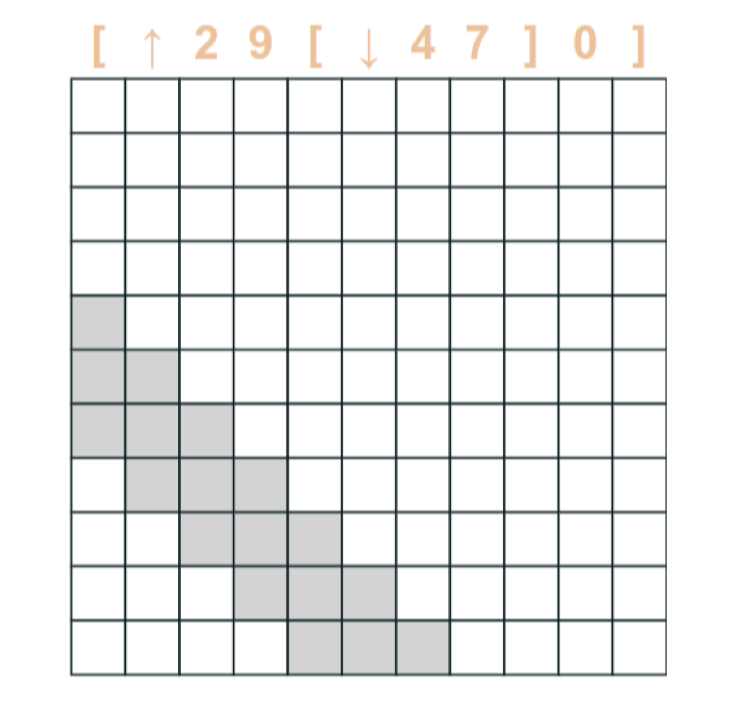
Task: Long Range Arena (ListOps)
Attention for Realistic Examples

The Problem with Attention
Computational Complexity
| Layer Type | Training | Inference |
|---|---|---|
| Attention | $\mathcal{O}(n^2) - parallel$ | $\mathcal{O}(n^2) - sequential$ |
| Recurrent | $\mathcal{O}(1) - sequential$ | $\mathcal{O}(1) - sequential$ |
State Space Models a.k.a Linear RNN
State Space Models

- SSM is a continuous-time, differential equation.
- $h$ is a vector-valued hidden state
Isn't this just an RNN?
- Discrete
- Non-linear
- Training: Slow (serial bottleneck)
- Gen: Fast (constant per step)
- Continuous
- Linear
- Training: Fast (parallelizable)
- Gen: Fast (constant per step)
Didn't we try RNNs already?
- The last major RNN model in NLP - ELMo
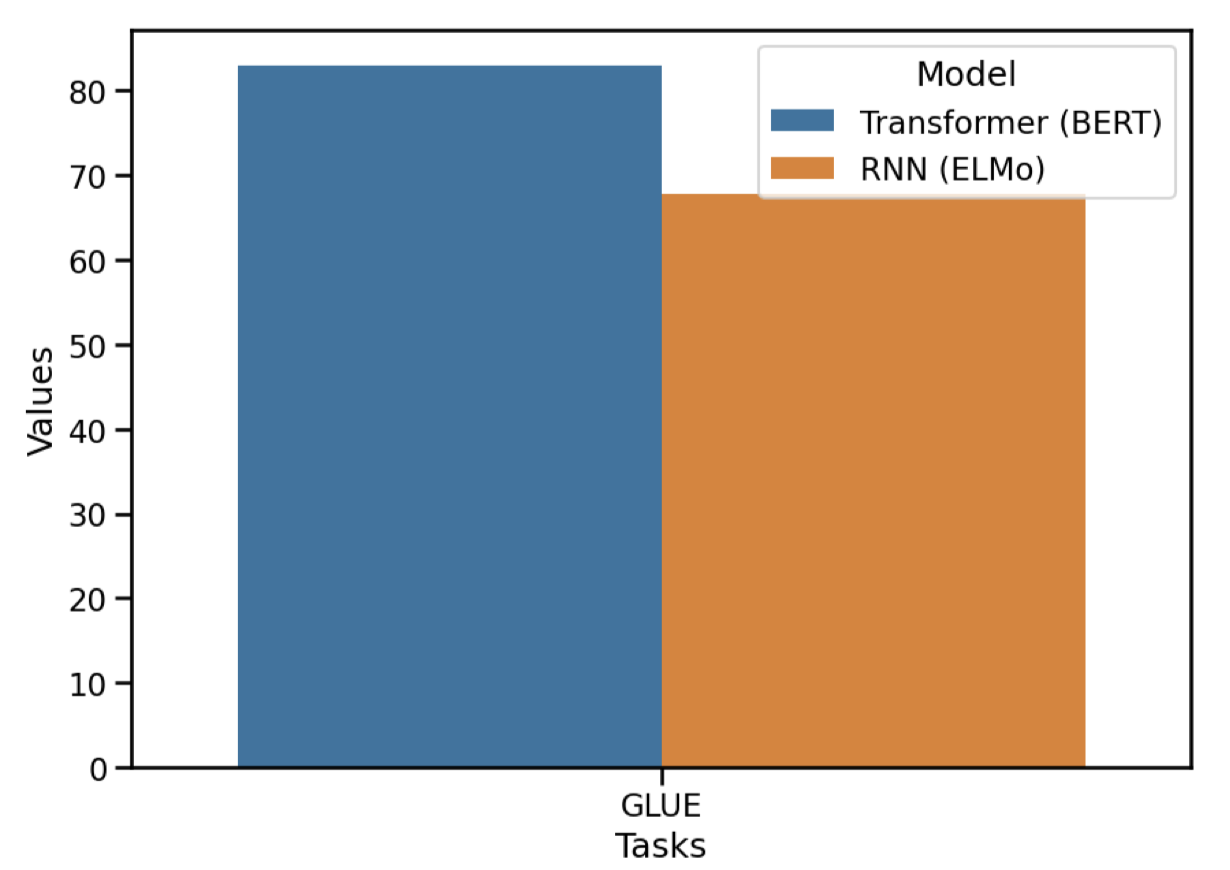
- [Peters et al., 2018, Devlin et al., 2018]
The Key to SSM
- Efficient Models
- Effective Long-Range Parametrizations
Discretizing SSMs
$$ \begin{align*} h'(t) &= \color{green}{\mathbf{A}} h(t) + \color{cyan}{\mathbf{B}}x(t) \\ y(t) &= \color{yellow}{\mathbf{C}}h(t) + \color{orange}{\mathbf{D}}x(t) \end{align*} $$- Discretize $A$, $B$, $C$, $D$
- Zero-Order Hold, Euler Method, Bilinear Transform
SSM through Sequential Scan
- Expansion of terms: $$ \begin{align*} y_k = \color{yellow}{\mathbf{\bar{C}}}h_k \quad h_k = \color{green}{\mathbf{\bar{A}}} h_{k-1} + \color{cyan}{\mathbf{\bar{B}}}x_k \end{align*} $$
h = 0
ylist = []
for i in range(sequence_length):
h = A @ h + B @ x[i]
y = C @ h
ylist.append(y)
SSM through Convolution
- Expansion of terms: $$ \begin{align*} y_k = \color{yellow}{\mathbf{\bar{C}}}h_k \quad h_k = \color{green}{\mathbf{\bar{A}}} h_{k-1} + \color{cyan}{\mathbf{\bar{B}}}x_k \end{align*} $$
- $$ \begin{align*} y_1 &= \color{yellow}{\mathbf{\bar{C}}}\color{cyan}{\mathbf{\bar{B}}}x_1 \\ y_2 &= \color{yellow}{\mathbf{\bar{C}}}\color{green}{\mathbf{\bar{A}}}\color{cyan}{\mathbf{\bar{B}}}x_1 + \color{yellow}{\mathbf{\bar{C}}}\color{cyan}{\mathbf{\bar{B}}}x_2 \\ y_3 &= \color{yellow}{\mathbf{\bar{C}}}\color{green}{\mathbf{\bar{A}}}\color{green}{\mathbf{\bar{A}}}\color{cyan}{\mathbf{\bar{B}}}x_1 + \color{yellow}{\mathbf{\bar{C}}}\color{green}{\mathbf{\bar{A}}}\color{cyan}{\mathbf{\bar{B}}}x_2 + \color{yellow}{\mathbf{\bar{C}}}\color{cyan}{\mathbf{\bar{B}}}x_3 \\ \end{align*} $$
- Convolutional parametrization: $$ \begin{align*} \bar{K} = \left(\color{yellow}{\mathbf{\bar{C}}}\color{cyan}{\mathbf{\bar{B}}}, \color{yellow}{\mathbf{\bar{C}}}\color{green}{\mathbf{\bar{A}}}\color{cyan}{\mathbf{\bar{B}}},\dots,\color{yellow}{\mathbf{\bar{C}}}\color{green}{\mathbf{\bar{A}}}^{L-1}\color{cyan}{\mathbf{\bar{B}}}\right) \end{align*} $$
SSM through Parallel Scan
- Sequence of interest: $$ \begin{align*} h_k = \color{green}{a_k}h_{k-1} + \color{cyan}{b_k} \end{align*} $$
- Compact form (assuming diagonal $\mathbf{\bar{A}}$): $$ \begin{align*} \log h_k &= \color{green}{a_k}^{*} + \log(x_0 + \color{cyan}{b_k}^{*}) \\ \color{green}{a_k}^{*} &= \sum_{k}^{cum} \log a_k \\ \color{green}{b_k}^{*} &= \sum_{k}^{cum} e^{\log b_k - a_k^*} \end{align*} $$
- Faster than sequential scan by $\frac{L}{\log L}$
- [Blelloch and Reif, 1990, Martin and Cundy, 2018, Smith et al., 2022]
- Franz A. Heinsen, "Efficient Parallelization of a Ubiquitous Sequential Computation," arXiv:2311.06281
SSM in Practice
- Extremely Poor...Barely learns
- Routing here must be static and regular (conv).
- Long convolution behavior is highly dependent on $\bar{A}$
$$
\begin{align*}
\bar{K} = \left(\color{red}{\mathbf{\bar{C}}}\color{blue}{\mathbf{\bar{B}}}, \color{red}{\mathbf{\bar{C}}}\color{green}{\mathbf{\bar{A}}}\color{blue}{\mathbf{\bar{B}}},\dots,\color{red}{\mathbf{\bar{C}}}\color{green}{\mathbf{\bar{A}}}^{L-1}\color{blue}{\mathbf{\bar{B}}}\right)
\end{align*}
$$
- Initialization of $\bar{A}$ is critical: stable and informative.
Getting SSMs to Work
Initializing SSM Parameters: HiPPO
- Summarize history in vector $x$ with Legendre coefficients
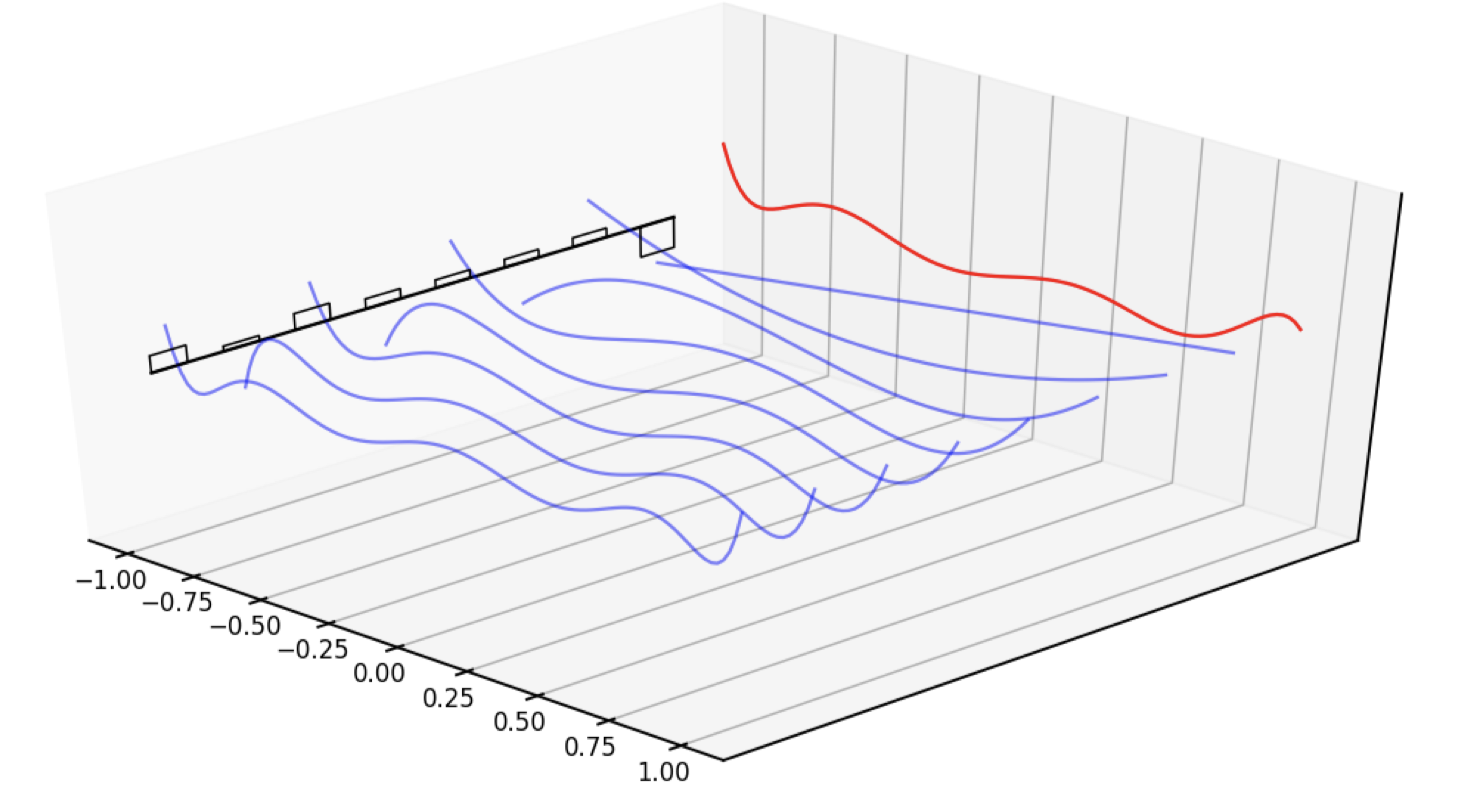
Initializing SSM Parameters: HiPPO
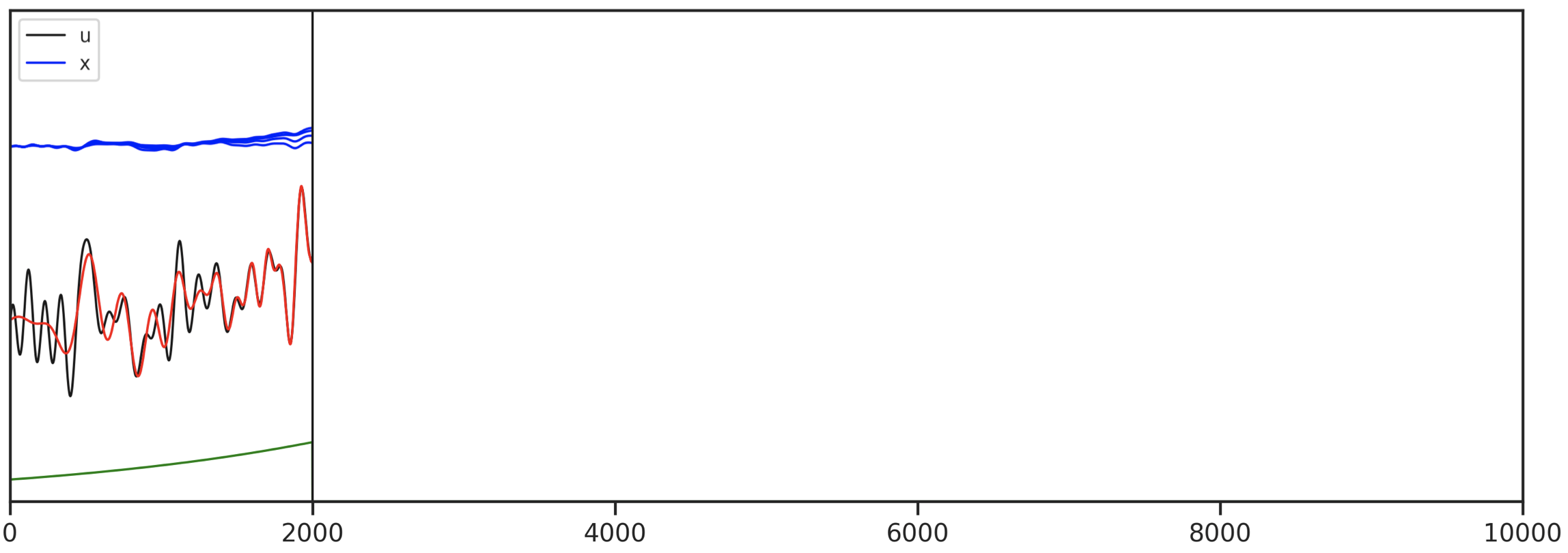
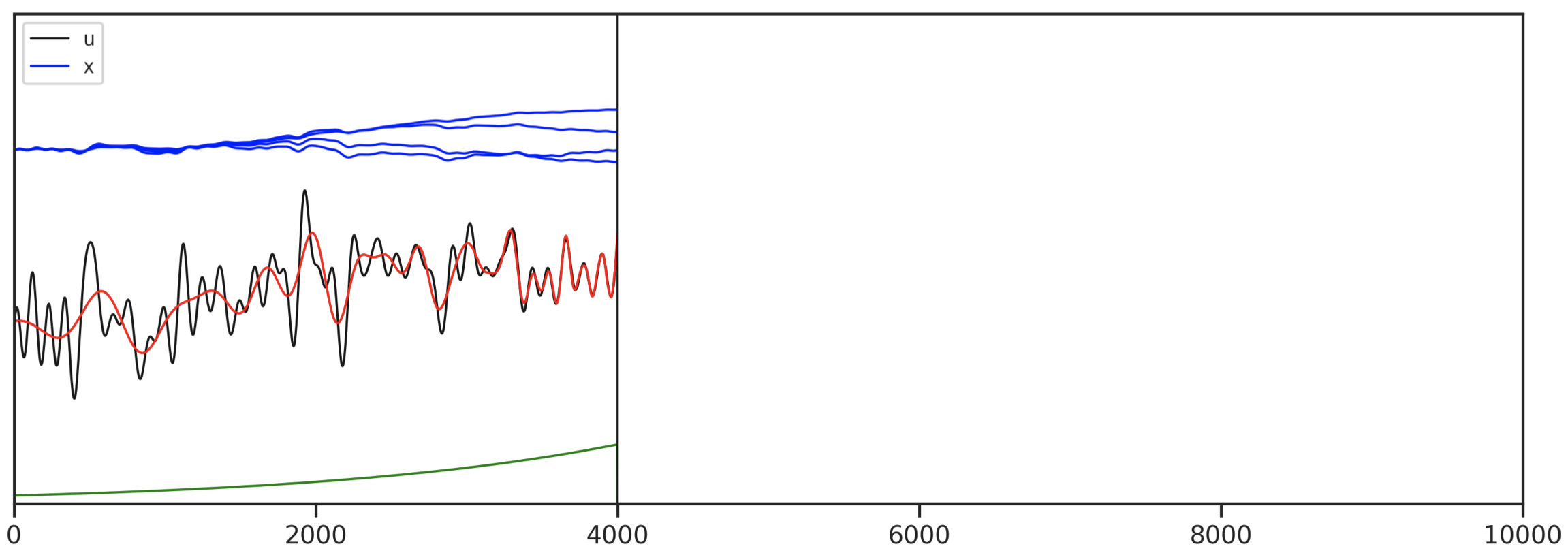
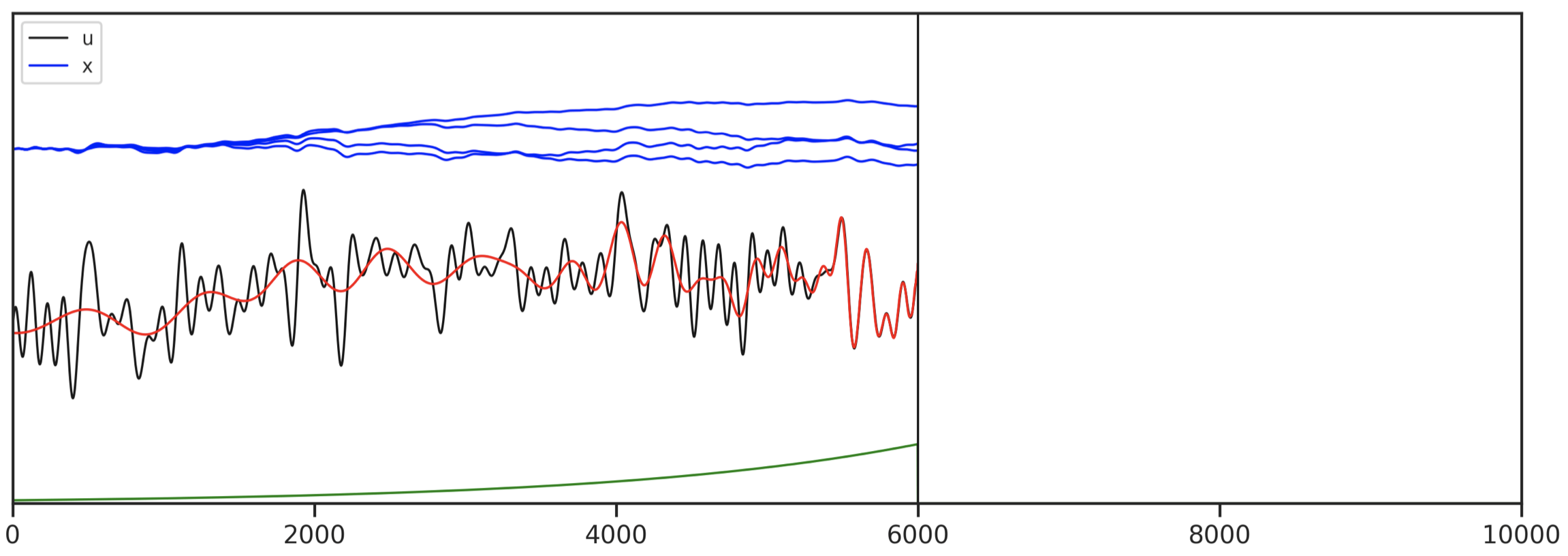
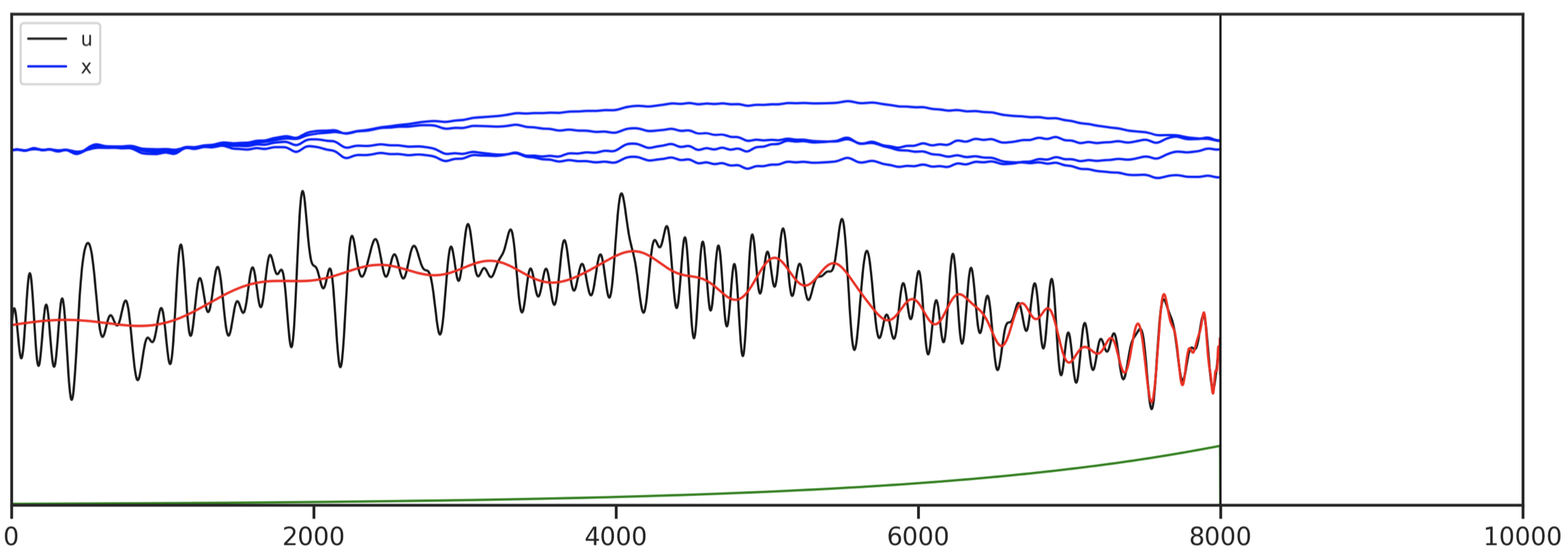
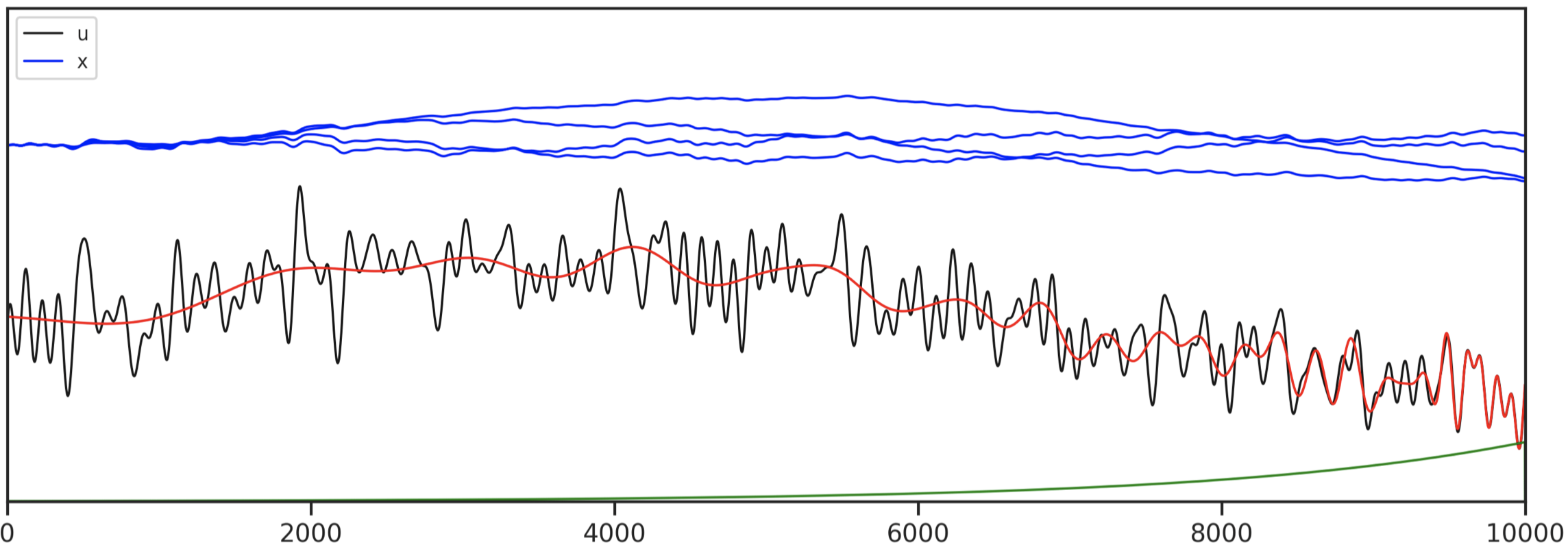
Results: ListOps
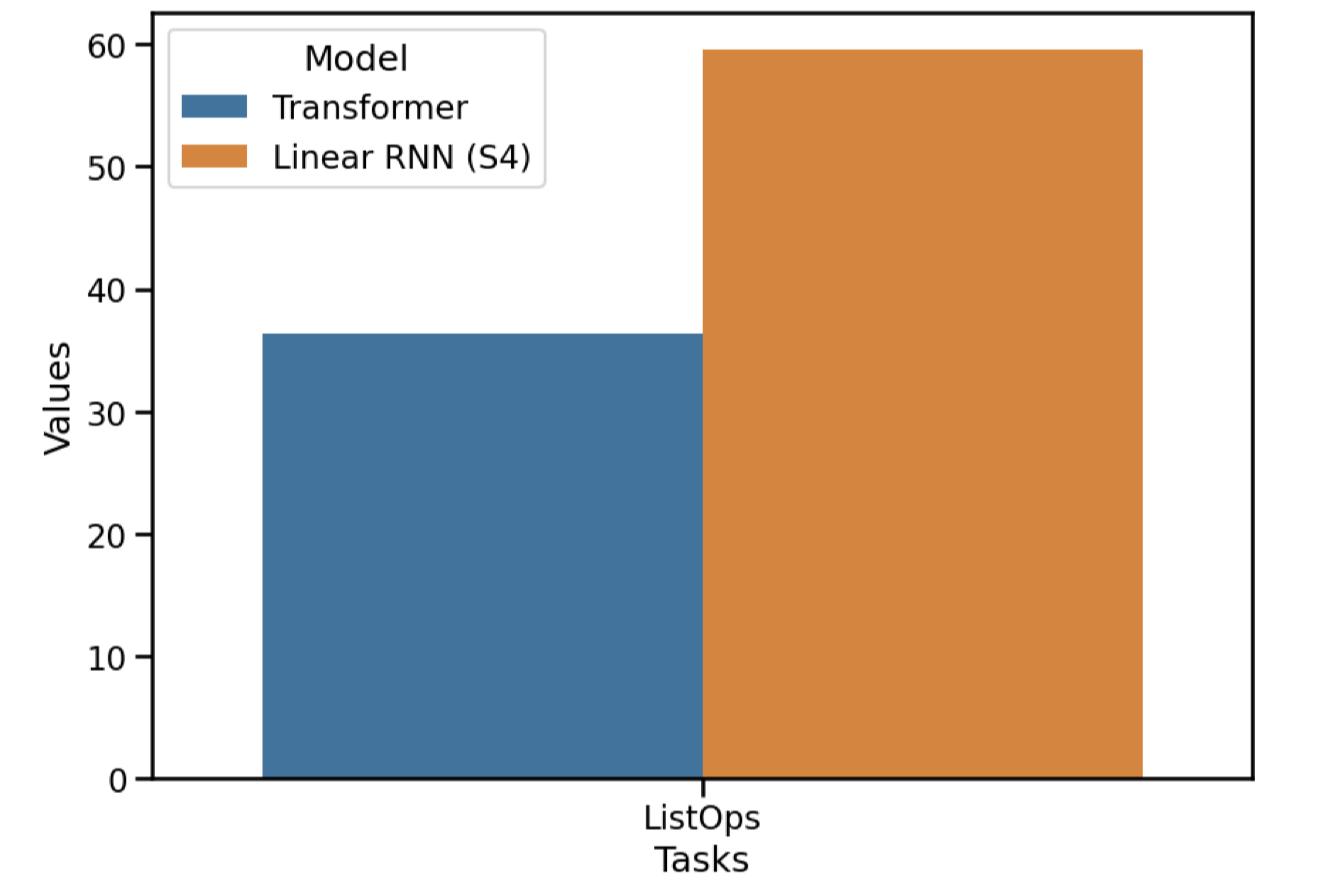
Results: Long Range Arena
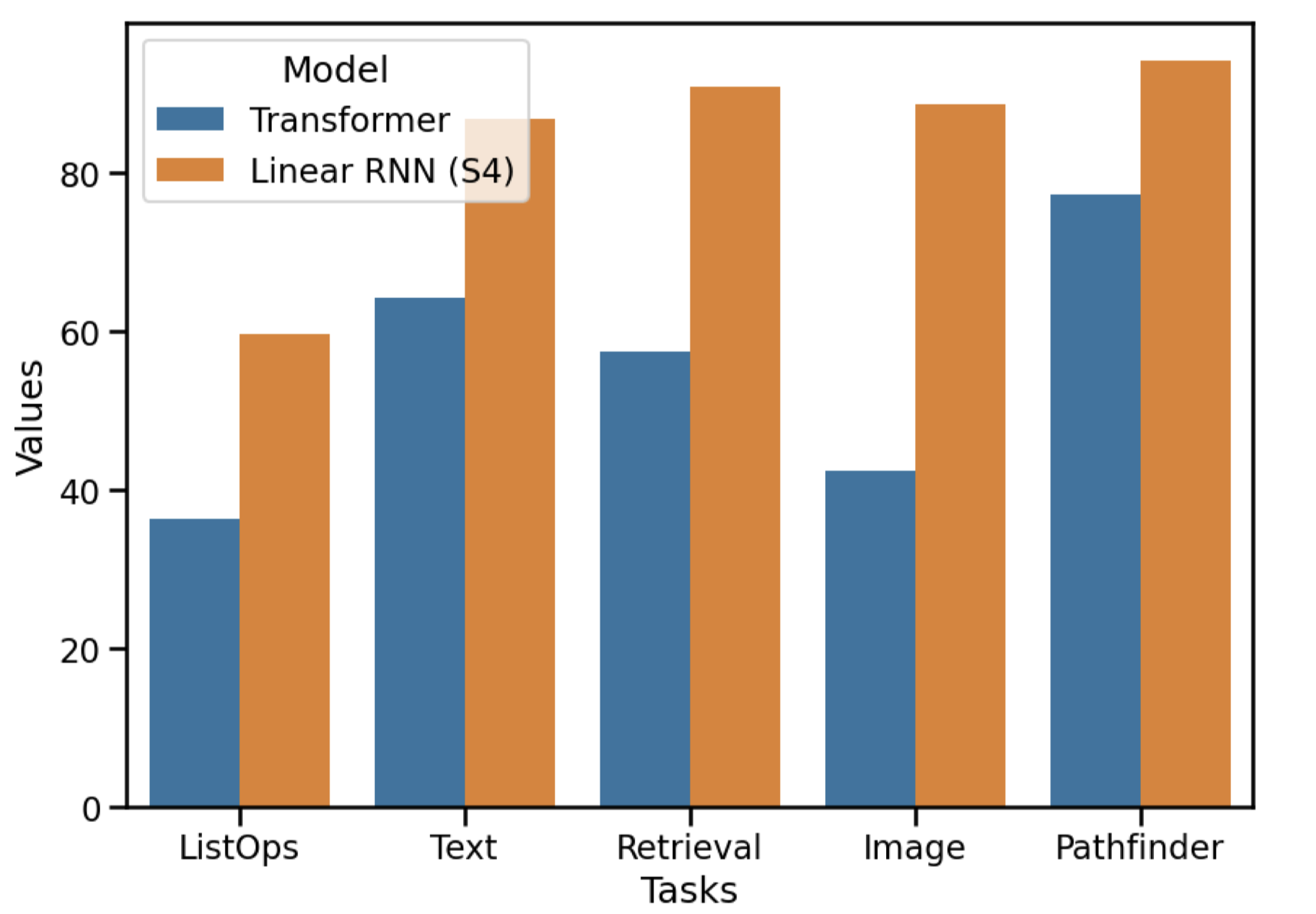
Selective State Space Models
Motivation
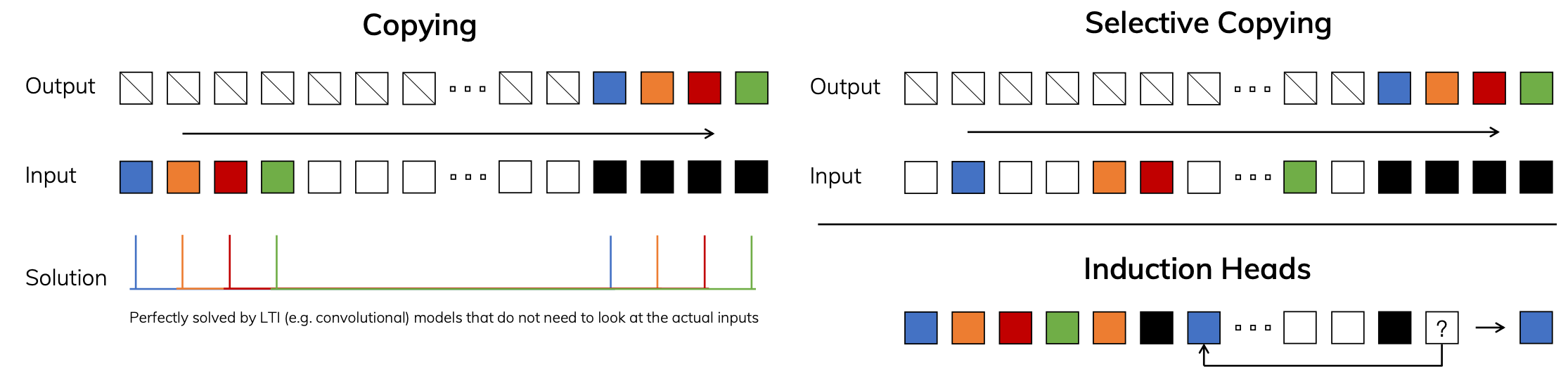
- SSM has fixed params $A,B,C,D$, attention is adaptive to input $x$.
- Make SSM params adaptive to input.
Key Ideas

- Convolutional view of SSM no longer valid.
- Need parallel associative scan.
- Custom CUDA implementation to overcome memory bottlenecks.
Mamba Architecture
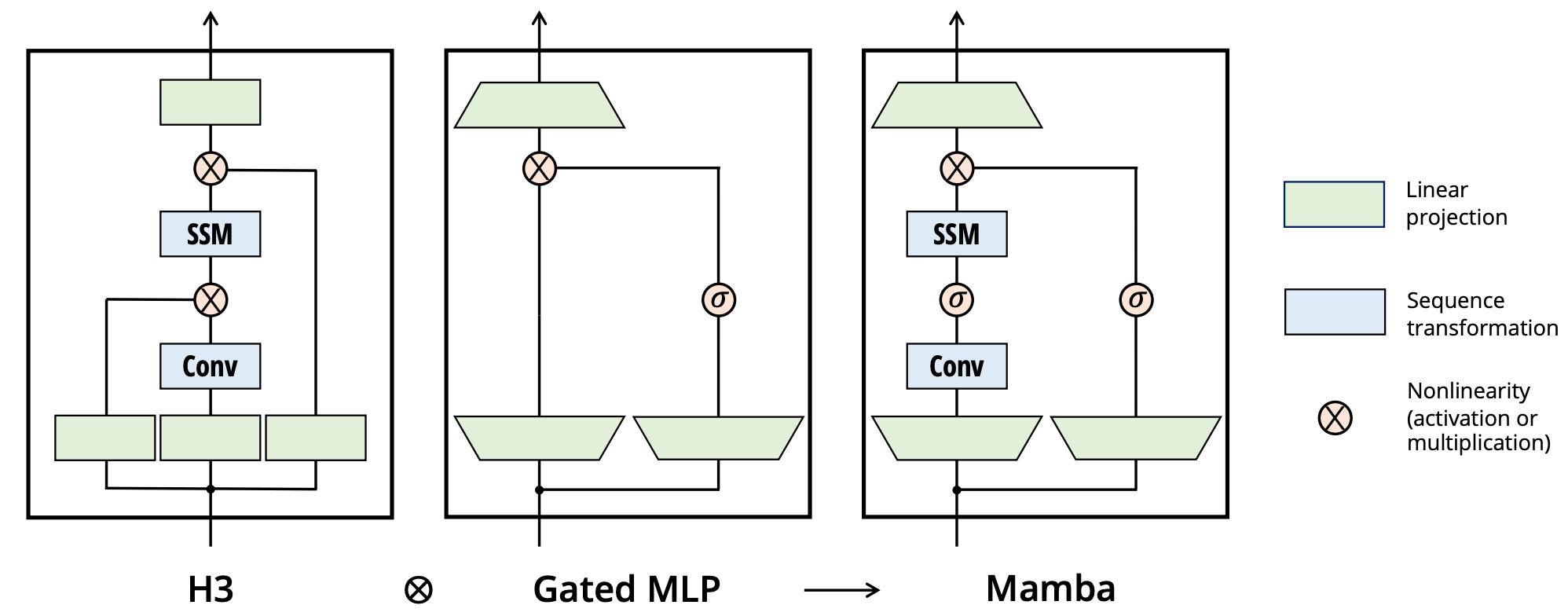
Mamba Overview
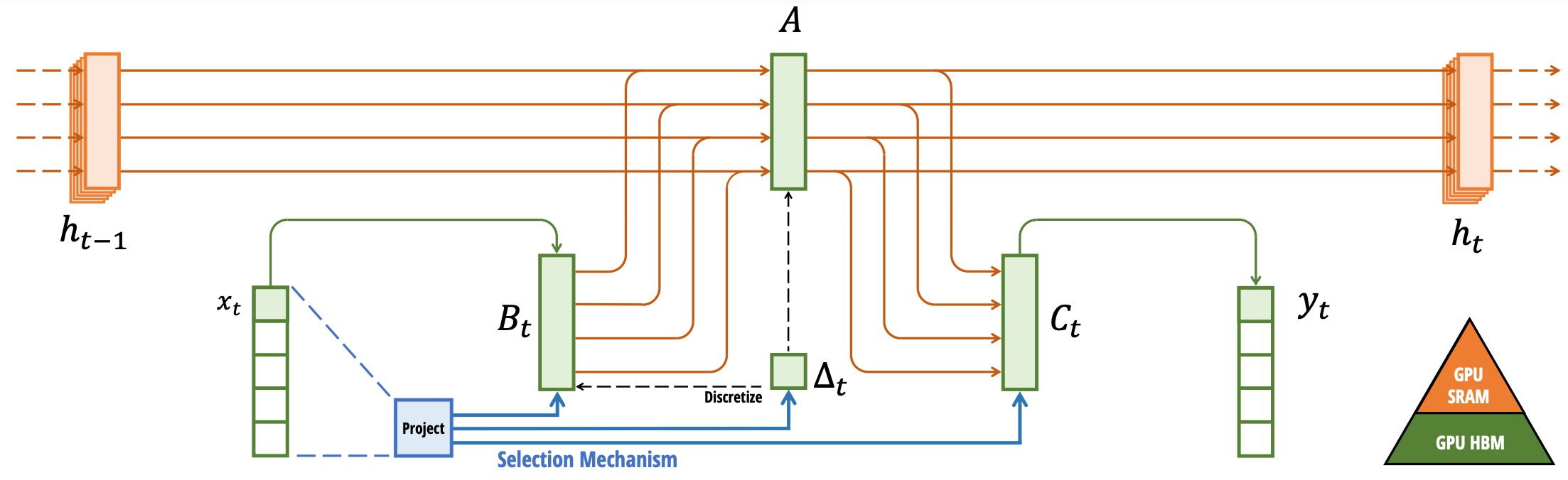
Why Mamba? Why Now?
- Contrasting trade-offs of transformers and RNNs highlight the crux of sequence modeling research: How can we improve model quality within the constraints of available compute?
- Recent progress in industry: rapid forward progress not from algorithmic breakthroughs but instead dramatic increases in compute.
One thing that should be learned from the bitter lesson is the great power of general purpose methods, of methods that continue to scale with increased computation even as the available computation becomes very great.
- Both RNNs and transformers, potentially, have a limited lifespan since they make poor use of compute.
- It is critical that we design models that better leverage compute while also maintaining or preserving fundamental model quality.
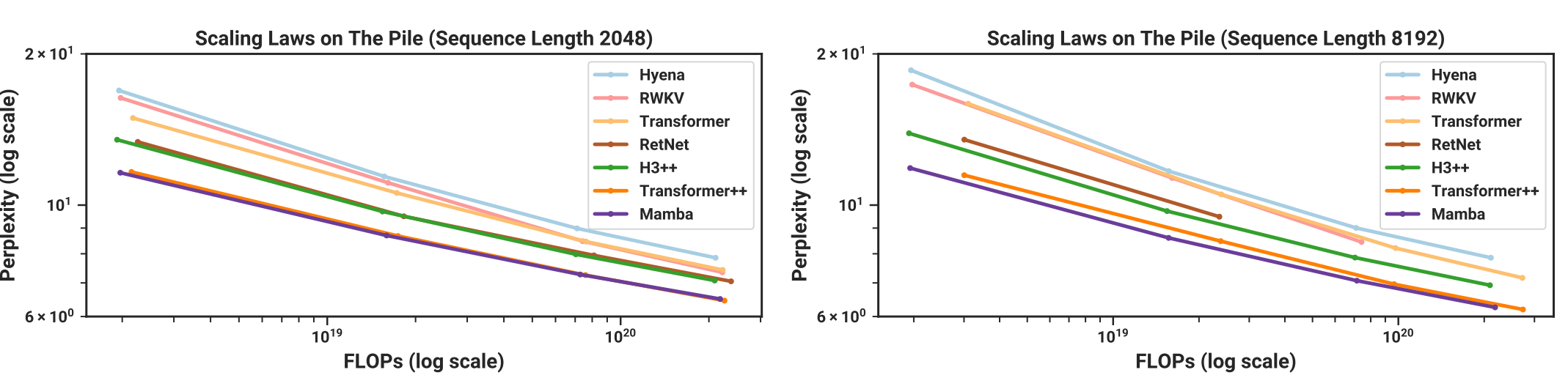
Comparing Attention with SSMs
Mamba Results
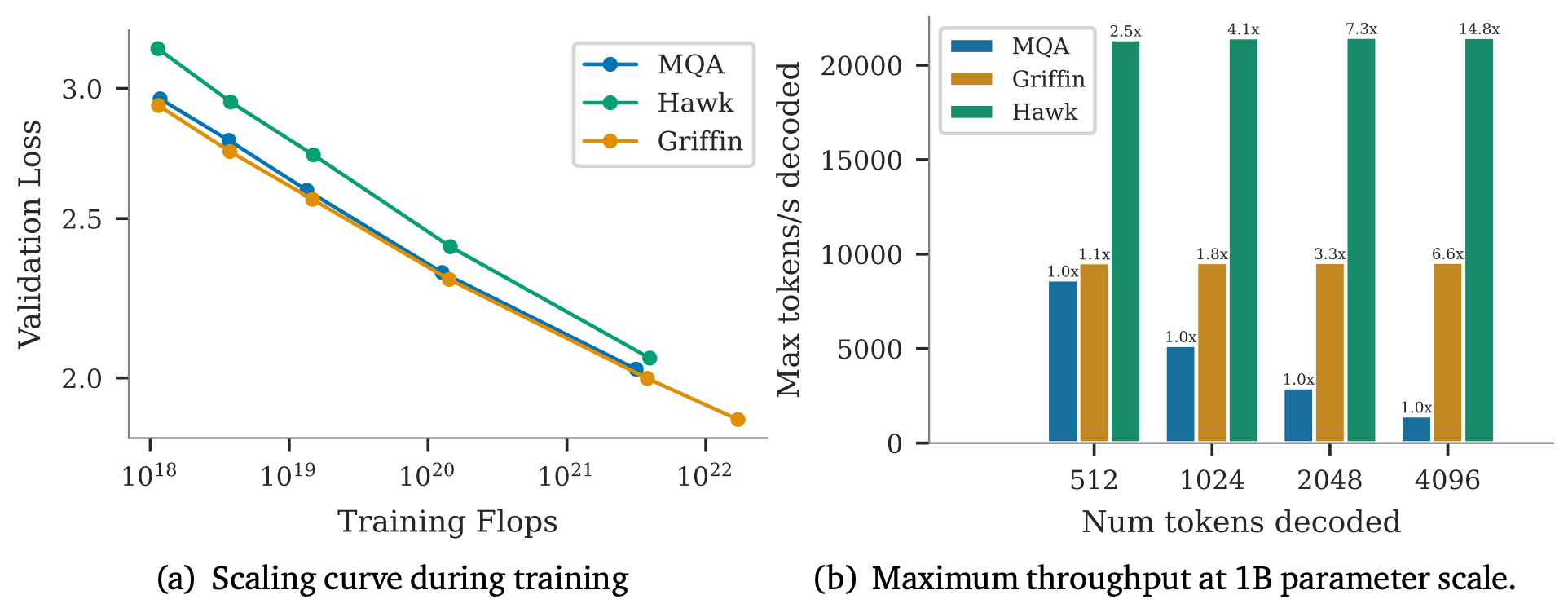
Results from Feb 2024: Hawk and Griffin
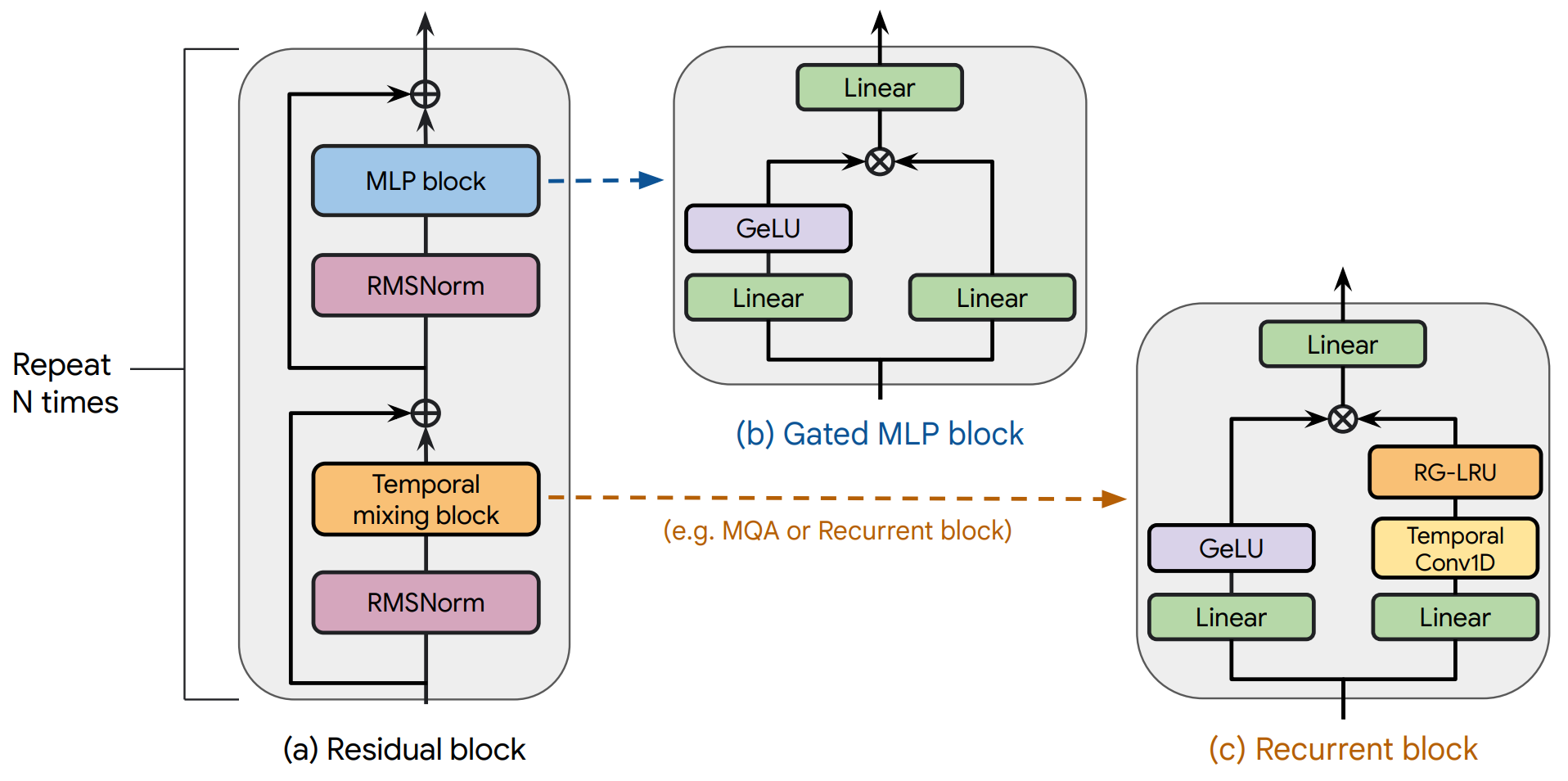
Results from Feb 2024: Hawk and Griffin
Results from Feb 2024: Based
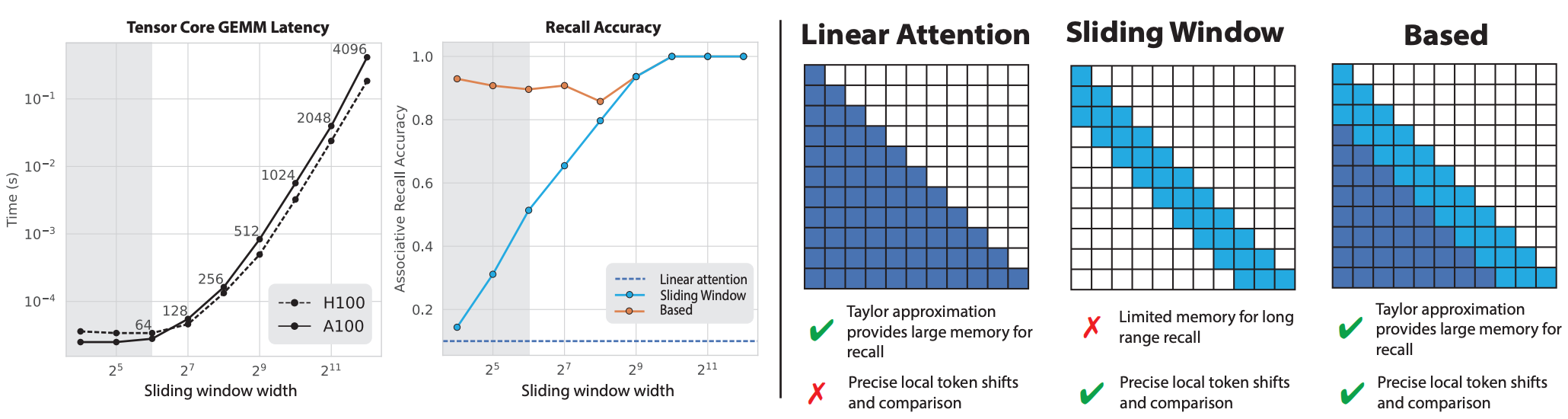
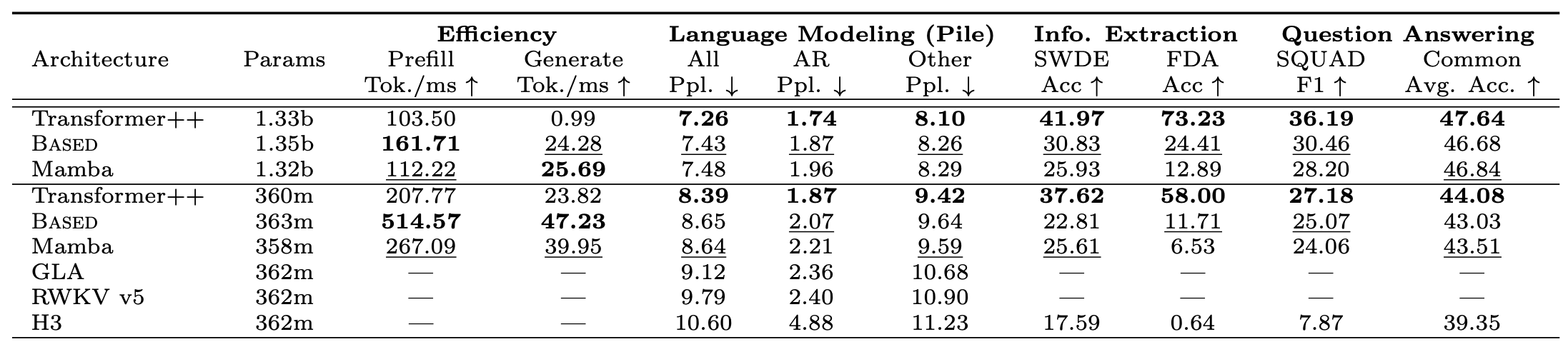
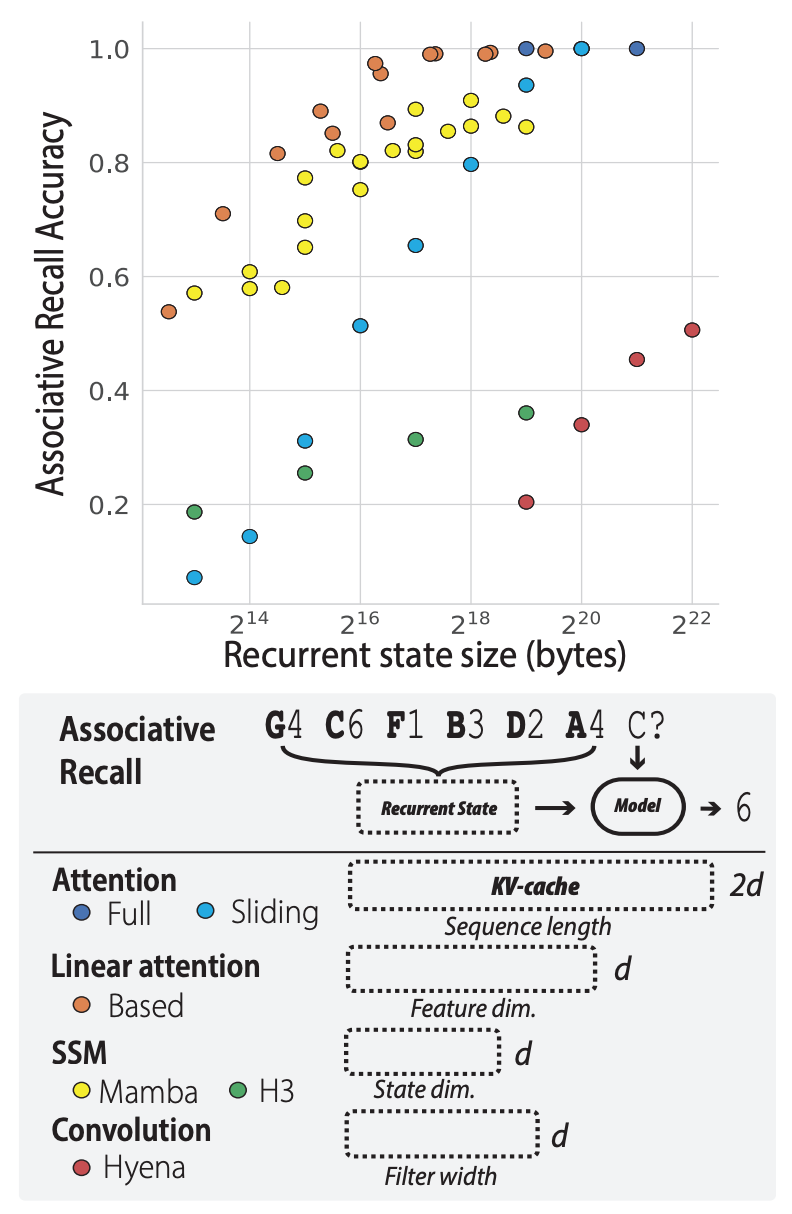
Lots of Progress on SSM
Summary
- Exciting progress on alternatives to attention layers.
- High demand for high-performance low-compute alternatives to attention.
- Next generation of architectures are likely to be based on pure SSM or SSM/attention hybrid.
- Open question: Is ability to model long context necessary for high performance models?