Graphs in the Real-World

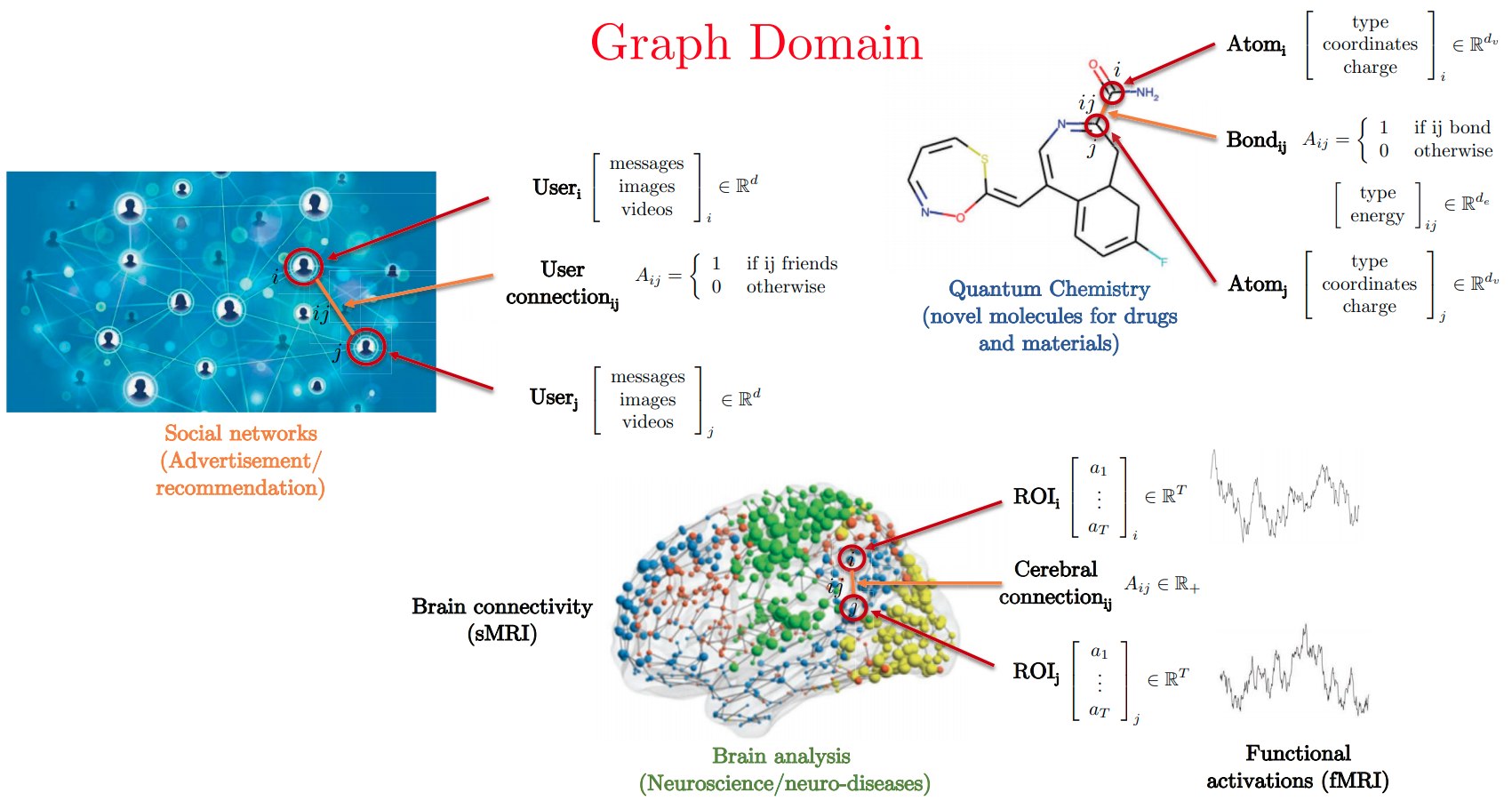
• Slide Credit: Xavier Bresson

Graph Structured Data

Standard CNN and RNN architectures don't work on this data.

• Slide Credit: Xavier Bresson

Molecules As Graphs

• Molecules can be represented by a graph
• Nodes: atoms
• Edges: bonds
• Features: atom type, charge, bond type

• Image Credit: Petar Veličković

GNN for Molecule Classification

• Task: predict whether a molecule is a potent drug
• binary classification to predict whether a drug will inhibit E.coli
• Train on curated dataset for molecules whose response is known

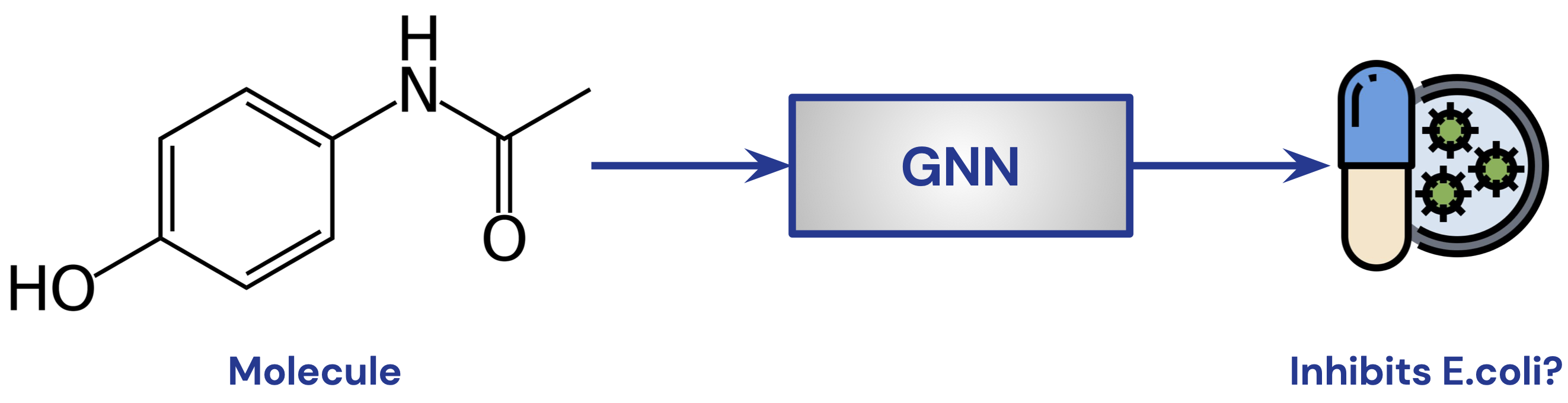
• Image Credit: Petar Veličković

Molecule: Real-World Success

• Once trained, GNN model can be applied to any molecule.
• Apply model on a large dataset of known candidate molecules
• Select the top 100 candidates from the GNN model
• manually evaluate selected candidates
• Success: discovered a previously overlooked compound that is a highly potent antibiotic

• A Deep Learning Approach to Antibiotic Discovery, Cell 2020

• Image Credit: Petar Veličković

Routing on Maps

• Transportation maps are naturally modelled as graphs
• Nodes: intersections
• Edges: roads
• Features: road length, current speed, historic speed

Routing on Maps

• Run GNN on supersegment graph to estimate time of arrival (graph regression)
• Already deployed in several major cities, significantly reduced negative ETA outcomes

GNNs from Scratch

Convolutional Neural Networks on Grids

• CNNs nicely exploit the grid structure of data.

• 2D convolutional operator as applied to a grid-structured input (e.g., image)

What about Graphs?

• What properties are useful for operating meaningfully on graphs?
• The nodes of a graph are not assumed to be in any order
• We would like to get the same results for two isomorphic graphs

• What symmetries and invariances must a GNN preserve?
• permutation invariance
• permutation equivariance

Learning on Sets

• Assume a set of nodes, without any edges.
• Let $\mathbf{x}_i \in \mathbb{R}^n$ be the feature of node $i$ i.e., $\mathbf{X}=(\mathbf{x}_1,\dots,\mathbf{x}_k)^T$
• we implicitly defined a node ordering
• would like our neural network to not depend on it
• Permutations change node-orderings.
• defined by a $n \times n$ permutation matrix
• has exactly one 1 in every row and column, and zeros everywhere else
• $\mathbf{X}' = \mathbf{P}\mathbf{X}$

Permutation Invariance

• Want to design $f(\mathbf{X})$ over sets that does not depend on the order.
• Want invariance to permutations i.e., for all permutation matrices $\mathbf{P}$:
• $f(\mathbf{PX})=f(\mathbf{X})$
• One very generic form is the Deep Sets model (Zaheer et al., NeurIPS 2017): $$f(\mathbf{X})=\phi\left(\sum_{i\in\mathcal{V}}\psi(\mathbf{x})\right)$$
• $\phi$ and $\psi$ are learnable functions, e.g., MLPs
• the sum is critical (other choices are max and avg)

Permutation Equivariance

• Permutation-invariance is good for obtaining set-level outputs
• In many problems we want node level predictions.
• need to identify node outputs, but permutation-invariant aggregator destroys it
• Need functions that doesn't change node order
• We need $f(\mathbf{X})$ to be permutation-equivariant, for all permutation matrices: $$f(\mathbf{PX})=\mathbf{P}f(\mathbf{X})$$

Learning on Sets

• Equivariance mandates that each node’s row is unchanged by f.
• equivariant set functions transform each node $\mathbf{x}_i$ into a latent vector $\mathbf{h}_i$ $$\mathbf{h}_i=\psi(\mathbf{x}_i)$$
• $\psi(\cdot)$ is applied to each node
• stacking $\mathbf{h}_i$ yields $H=f(\mathbf{X})$
• Recipe: combine equivariant functions with invariant functions $$f(\mathbf{X})=\phi\left(\bigoplus_{i\in\mathcal{V}}\psi(\mathbf{x}_i)\right)$$
• $\bigoplus$ is a permutation invariant operator (e.g., sum, max, avg)

Learning on Graphs

Permutation Invariance and Equivariance on Graphs

• Key Difference: node permutations act accordingly on the edges
• Need to permute both rows and columns of $\mathbf{A}$
• apply permutation matrix as $\mathbf{PAP}^T$


• Invariant and equivariant functions $f(\mathbf{X},\mathbf{A})$ on graphs:
• Invariance: $f(\mathbf{PX},\mathbf{PAP}^T)=f(\mathbf{X},\mathbf{A})$
• Equivariance: $f(\mathbf{PX},\mathbf{PAP}^T)=Pf(\mathbf{X},\mathbf{A})$

Locality on Graphs

• On sets, equivariance was enforced by applying functions to every node in isolation.
• On graphs, broader context is given by a node's neighbourhood
• For a node $i$, we can define its (1-hop) neighbourhood as: $$\mathcal{N}_i=\{j: (i,j)\in\mathcal{E} \vee (j,i) \in \mathcal{E}\}$$
• We can extract a multiset of features in the neighborhood $$\mathbf{X}_{\mathcal{N}_i}=\{\{\mathbf{x}_j: j\in \mathcal{N}_i\}\}$$
• define a local function $g$ that operates on the multiset $g(\mathbf{x}_i, \mathbf{X}_{\mathcal{N}_i})$

How to use GNNs?

Recipe for graph neural networks

• Construct permutation equivariant functions, $f(\mathbf{X},\mathbf{A})$, by appropriately applying a local function, $g$, over all neighbourhoods:
$$f(\mathbf{X}, \mathbf{A})=\begin{bmatrix} - & g(\mathbf{x}_1, \mathbf{X}_{\mathcal{N}_1}) & - \\ - & g(\mathbf{x}_2, \mathbf{X}_{\mathcal{N}_2}) & - \\ & \vdots & \\ - & g(\mathbf{x}_n, \mathbf{X}_{\mathcal{N}_n}) & - \end{bmatrix}$$
• For equivariance, we ensure $g$ does not depend on order of the vertices in $\mathbf{X}_{\mathcal{N}_i}$
• i.e., $g$ should be permutation invariant

Recipe for graph neural networks

$X_{\mathcal{N}_b}=\{\{\mathbf{x}_a, \mathbf{x}_b, \mathbf{x}_c, \mathbf{x}_d, \mathbf{x}_e\}\}$

GNN Pipeline

• Standard GNN Pipeline:
• Input Layer: Linear embedding of input node/edge features.
• GNN Layers: Apply favorite GNN layer $L$ times.
• Task-based layer : Graph/node/edge prediction layer.

GNN Pipeline

• Slide Credit: Xavier Bresson

GNN Pipeline

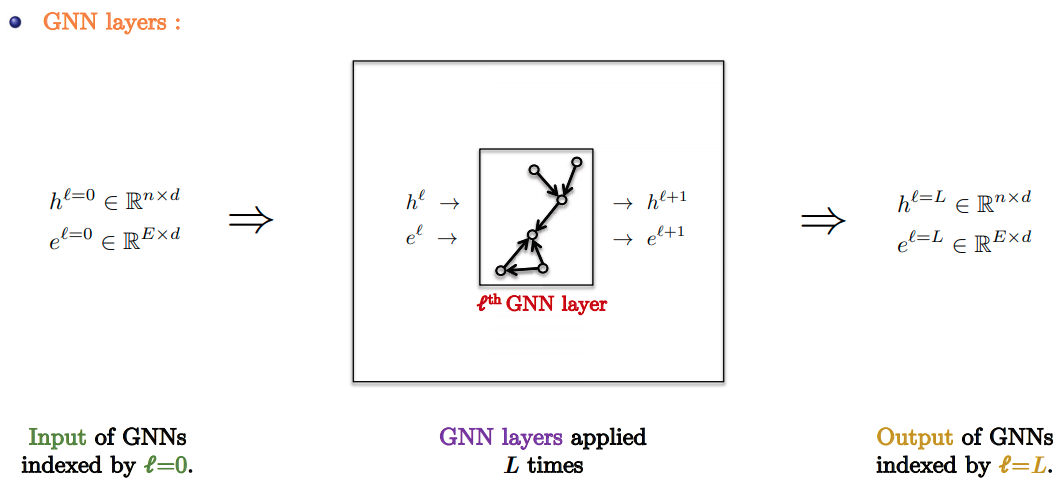
• Slide Credit: Xavier Bresson

GNN Pipeline

• Slide Credit: Xavier Bresson