Score Matching and Diffusion Models

Score Matching and Diffusion Models - IV

CSE 849: Deep Learning

Vishnu Boddeti

Today

Sampling from Diffusion Models
Solving Inverse Problems with Diffusion Models
Latent Diffusion
Personalization
ControlNet
Flow Matching

Sampling from Diffsion Models

Classifier Guidance

Slide Credit: Arash Vahdat

Classifier-Free Guidance

Slide Credit: Arash Vahdat

Text Guidance

Slide Credit: Arash Vahdat

Inverse Problems

Diffusion Posterior Sampling

Diffusion Posterior Sampling (DPS) for general noisy inverse problems.

Conditional Sampling

Let $A$ be a linear operator for an inverse problem (masking operator for inpainting, blur operator for deblurring, subsampling for SR, etc.).
The observation model is, $$\mathbf{y} = A\mathbf{x}_{unknown} + \mathbf{\epsilon}, \quad \mathbf{\epsilon} \sim \mathcal{N}(0, \sigma^2I).$$
We would like to sample, $$p_0(\mathbf{x}_0|A\mathbf{x}_0 + \mathbf{\epsilon} = \mathbf{y}) = p_0(\mathbf{x}_0|\mathbf{y})$$ to estimate $\mathbf{x}_{unknown}$ with the prior of the generative model.

Conditional Sampling Continued...

From (Song et al. 2021), we can consider the SDE for the conditional distribution $p_0(\mathbf{x}_0|\mathbf{y})$:
Backward diffusion for VP_SDE: $\mathbf{y}_t = \mathbf{x}_{T-t}$ $$d\mathbf{y}_t = [\beta_{T-t}\mathbf{y}_t + \beta_{T-t}\nabla_{\mathbf{x}=\mathbf{y}_t}\log p_{T-t}(\mathbf{y}_t|\mathbf{y})]dt + \beta{T-t}d\mathbf{w}_t.$$
By Bayes rule: $$\log p_{T-t}(\mathbf{y}_t|\mathbf{y})=\log p_{T-t}(\mathbf{y}|\mathbf{y}_t) + \log(p_{T-t}(\mathbf{y}_t)) - \log(p_{T-t}(\mathbf{y}))$$
Thus, $$\nabla_{\mathbf{x}==\mathbf{y}_t}\log p_{T-t}p(\mathbf{y}_t|\mathbf{y}) = \underbrace{\nabla_{\mathbf{x}=\mathbf{y}_t}\log p_{T-t}(\mathbf{y}_t|\mathbf{y})}_{\color{orange}{\text{intractable}}} + \underbrace{\nabla_{\mathbf{x}=\mathbf{y}_t}\log(p_{T-t}(\mathbf{y}_t))}_{\color{green}{\text{usual score function}}}$$
For clarity, $$\nabla_{\mathbf{x}==\mathbf{y}_t}\log p_{T-t}p(\mathbf{y}_t|\mathbf{y}) = \nabla_{\mathbf{x}=\mathbf{x}_t}\log p_{t}(\mathbf{y}|\mathbf{x}_t)$$

Conditional Sampling Continued...

(Chung et al., 2023) propose the following approximation: $$\log p_t(\mathbf{y}|\mathbf{x}_t) \approx \log p_t(\mathbf{y}|\mathbf{x}_0=\hat{\mathbf{x}}_0(\mathbf{x}_t,t))$$ with $\hat{\mathbf{x}}_0(\mathbf{x}_t,t)$ the estimate of the original image from the network.
Since $$p(\mathbf{y}|\mathbf{x}_0) = \frac{1}{(2\pi\sigma)^{\frac{n}{2}}}\exp\left(-\frac{\|\mathbf{y}-A\mathbf{x}_0\|}{2\sigma^2}\right)$$ we finally approximate $$\nabla_{\mathbf{x}=\mathbf{x}_t}\log p_t(\mathbf{y}|\mathbf{x}_t) = -\frac{1}{2\sigma^2}\nabla_{\mathbf{x}_t}\|\mathbf{y}-A\bar{\mathbf{x}}_0(\mathbf{x}_t,t)\|^2$$
Computing $\nabla_{\mathbf{x}_t}\|\mathbf{y} - A\hat{\mathbf{x}}_0(\mathbf{x}_t,t)\mathbf{x_0}\|^2$ involves a back propagation through the UNet.
So the conditional sampling will be twice as expensive as the sampling procedure.

Diffusion Posterior Sampling

Usual DDPM sampling (notation with $\hat{\mathbf{x}}_0(\mathbf{x}_t,t)$ instead of $\epsilon_{\theta}(\mathbf{x}_t,t)$) $$\mu_{\theta}(\mathbf{x}_t,t)=\frac{1}{\sqrt{\alpha_t}}\left(\mathbf{x}_t-\frac{\beta_t}{\sqrt{1-\bar{\alpha}}_t}\epsilon_{\theta}(\mathbf{x}_t,t)\right) = \frac{\sqrt{\alpha}_t(1-\bar{\alpha}_{t-1})}{1-\bar{\alpha}_t}\mathbf{x}_t + \frac{\sqrt{\bar\alpha}_{t-1}\beta_t}{1-\alpha}\hat{\mathbf{x}}_0(\mathbf{x}_t,t)$$
Add a correction term to drive $A\hat{\mathbf{x}}_0(\mathbf{x}_t,t)$ close to $\mathbf{y}$.
In practice $\zeta_i=\zeta_t=\|\mathbf{y}-A\bar{\mathbf{x}}_0(\mathbf{x}_t,t)\|^{-1}$.

Diffusion Posterior Sampling: Inpainting

Very good results in terms of perceptual metric (LPIPS).
Lack symmetry
It can sometimes be really bad though!

RePaint

Conditional DDPM for Super-Resolution

Super-resolution is often used to improve the quality of generated images.
One can train a speciﬁc DDPM for this task by conditioning the Unet with the low resolution image $\epsilon_{\theta}(\mathbf{x}_t,\mathbf{y}_{LR},t)$.

(Saharia et al., 2023) To condition the model on the input $\mathbf{y}_{LR}$, we upsample the low-resolution image to the target resolution using bicubic interpolation. The result is concatenated with $\mathbf{x}_t$ along the channel dimension.

Conditional DDPM for Super-Resolution

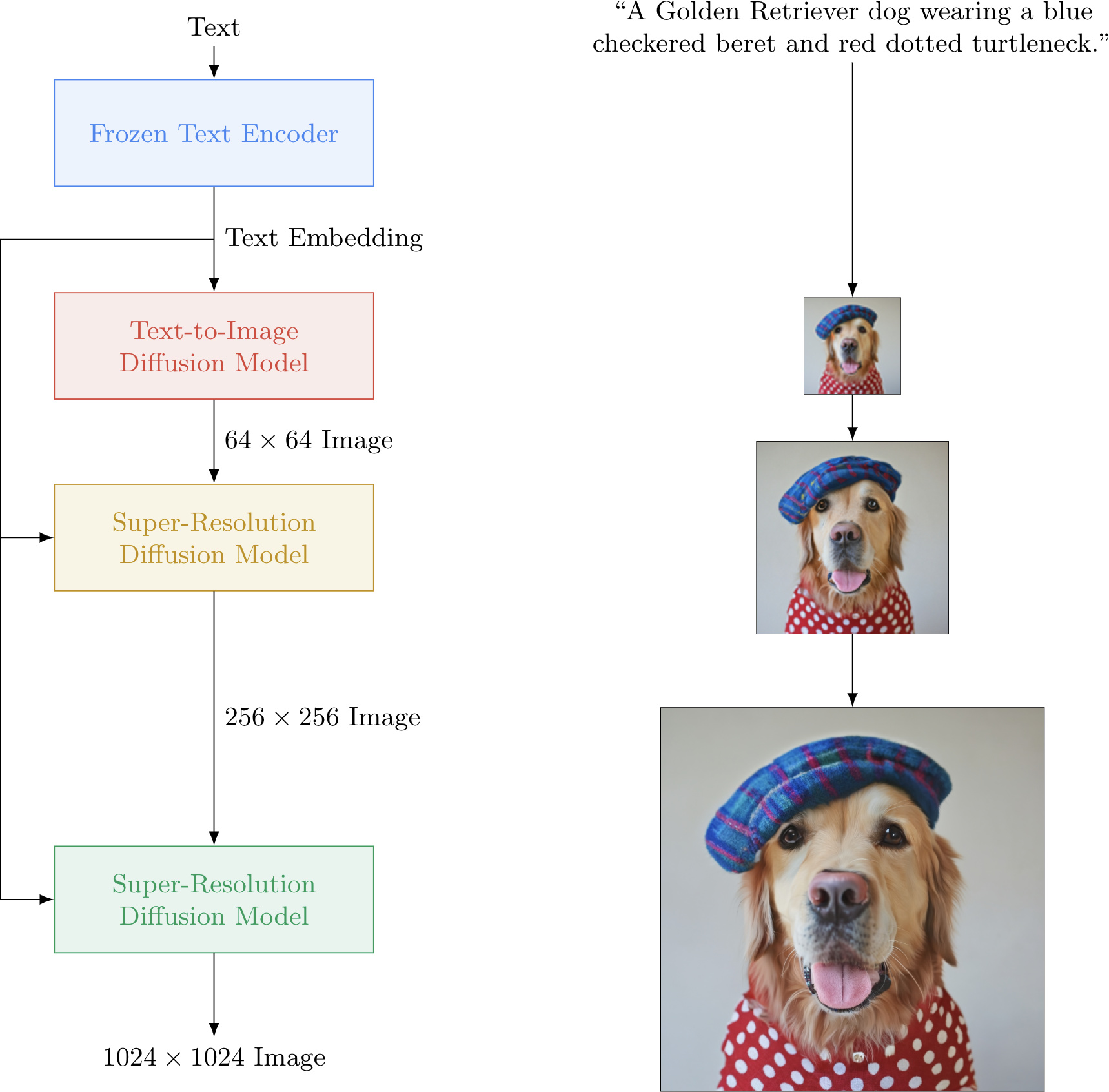
Imagen pipeline: Text conditioning & Conditional super-resolution via DDPM.

(Saharia et al., 2022)

Latent Diffusion Model

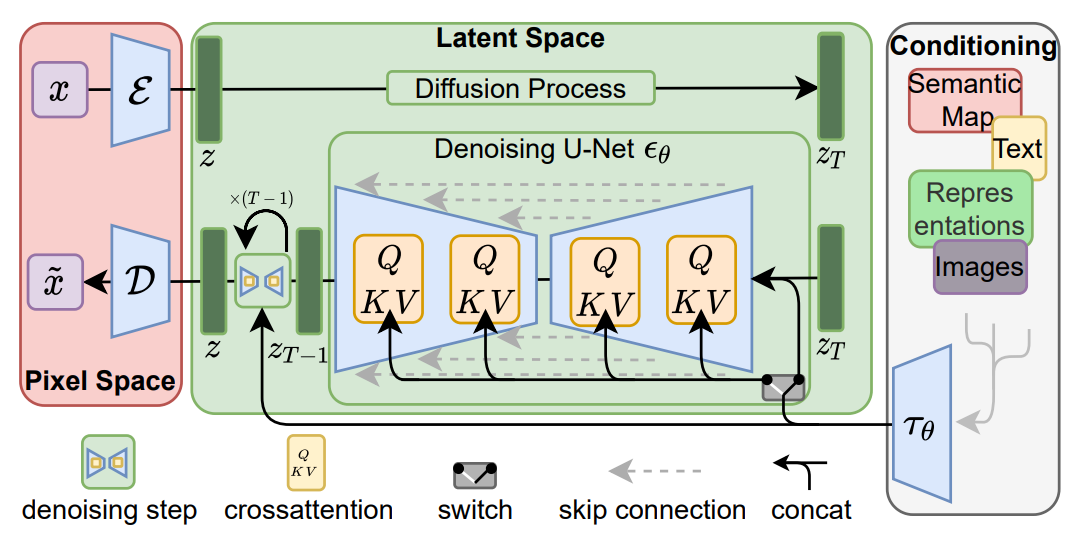
The distribution of latent embeddings close to Normal distribution -> Simpler denoising, Faster Synthesis!
(2) Augmented latent space -> More expressivity!
Tailored Autoencoders -> More expressivity, Application to any data type (graphs, text, 3D data, etc.)!

Latent Diffusion Model: Results

Latent Diffusion Model: AutoEncoder

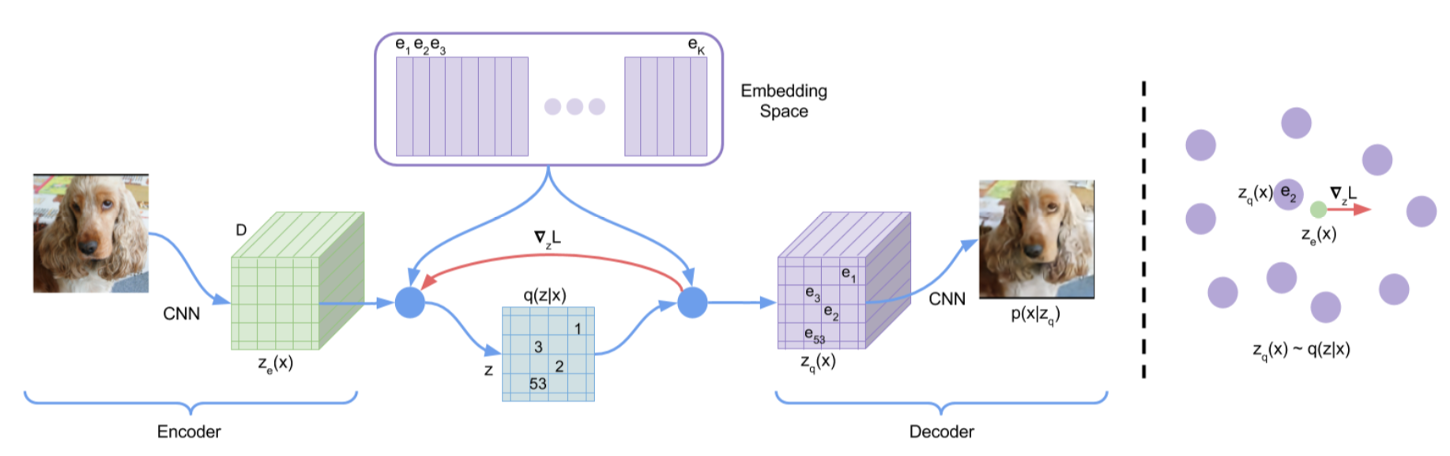\begin{equation} L = \log p(x|z_q(x)) + \|sg[z_e(x)]-e\|_2^2 + \beta\|z_e(x)-sg[e]\|_2^2 \end{equation} Neural Discrete Representation Learning, NeurIPS 2017

Video Diffusion Model

Welcome to the Future, Today!

Controlling Latent Diffusion Models

ControlNet

Adding Conditional Control to Text-to-Image Diffusion Models, ICCV 2023

ControlNet: How it Works

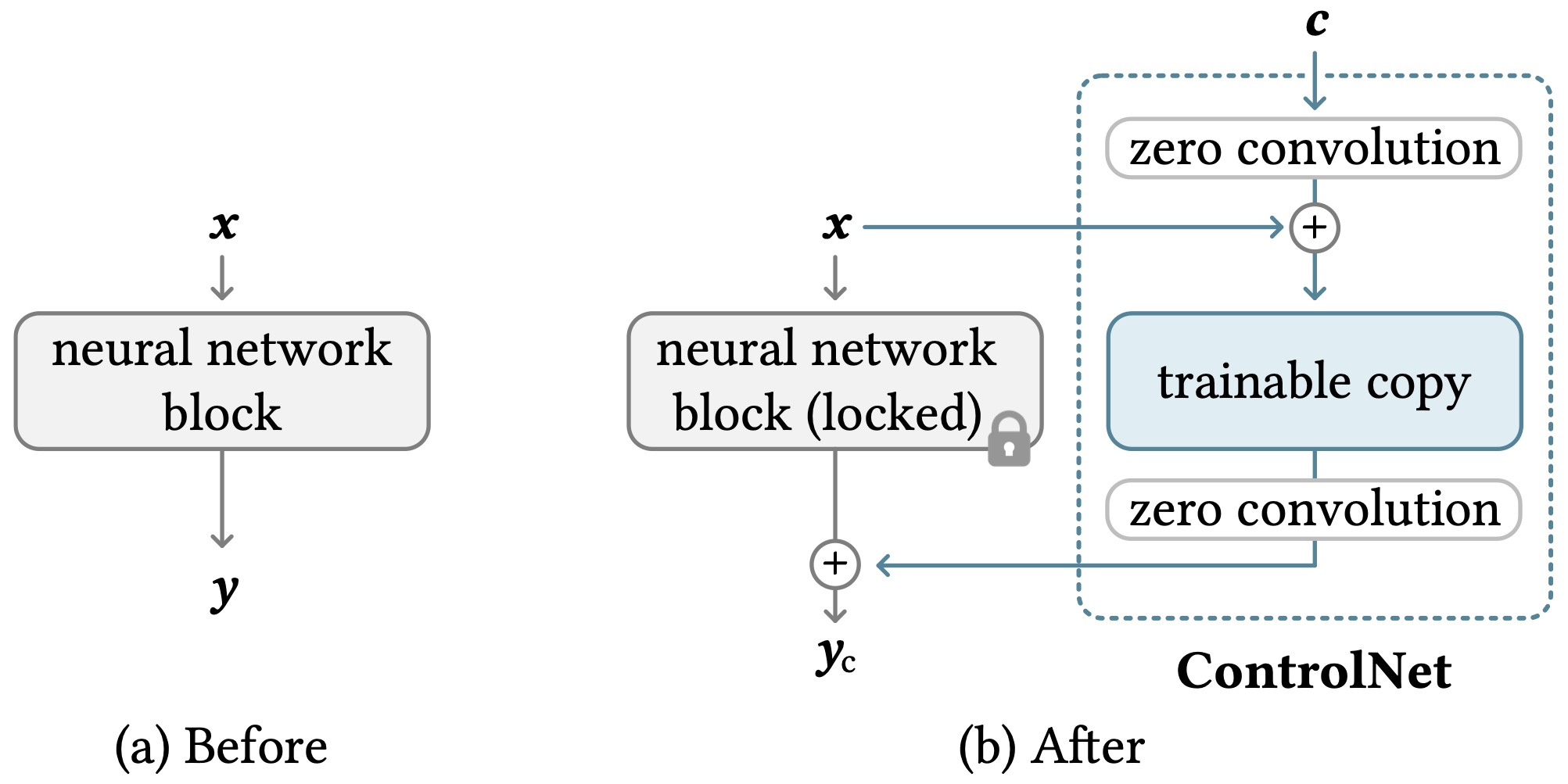
Adding Conditional Control to Text-to-Image Diffusion Models, ICCV 2023

ControlNet

Adding Conditional Control to Text-to-Image Diffusion Models, ICCV 2023

Flow Matching Models

Flows as Generative Models

Slide Credit: Yaron Lipman

Training Flow Models

$$\min D_{KL}(q||p) = -\mathbb{E}_{x\sim q}\color{red}{\log p_1(x)}+c$$

Continuity Equation (fixed x): $$\frac{\partial p_t}{\partial t} = -\nabla\cdot(p_tv_t)$$
Instantaneous change of coordinates (trajectory $x_t$) $$\color{red}{\frac{d\log p_t(x_t)}{dt} = -\nabla\cdot v_t(x_t)}$$

Problem: Needs forward simulation.

Neural Ordinary Differential Equations

We want a simulation free flow matching method

Flow Matching

Slide Credit: Yaron Lipman

Flow Matching

Slide Credit: Yaron Lipman

Flow Matching

Slide Credit: Yaron Lipman

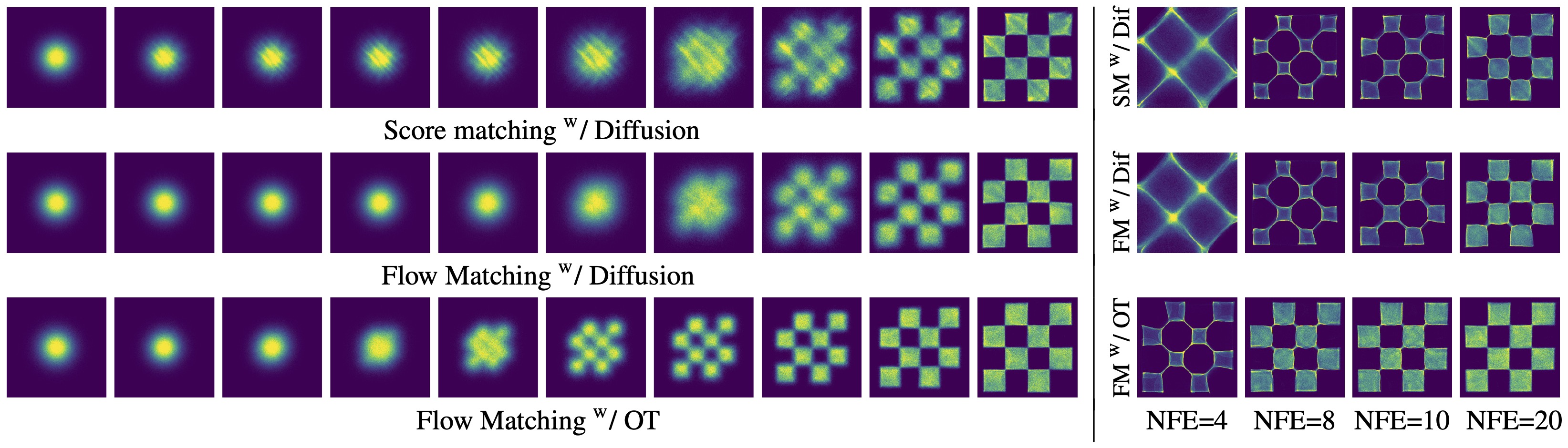
Flow Matching Vector Field

Flow Matching: Random Pairing $$ \begin{aligned} z &= (x_0, x_1) \\ q(z) &= q(x_0)q(x_1) \\ p_t(x|z) &= \mathcal{N}(x; tx_1 + (1-t)x_0, \sigma^2) \\ u_t(x|z) &= x_1 - x_0 \end{aligned} $$

Flow Matching: Optimal Transport Pairing $$ \begin{aligned} z &= (x_0, x_1) \\ q(z) &= \pi(x_0, x_1) \\ p_t(x|z) &= \mathcal{N}(x; tx_1 + (1-t)x_0, \sigma^2) \\ u_t(x|z) &= x_1 - x_0 \end{aligned} $$

External Resources

CVPR 2022 Tutorial

CVPR 2023 Tutorial

The Beginning of the End

Parting Thoughts

Diffusion Models:

(Latent) diffusion models have become a mature framework for generative modeling.
They are large models that require very long training with very large datasets.
But once trained they can be used as generic image priors.

Latent Diffusion Models:

Latent diffusion models allow for new image editing/generation techniques.
Bridge between NLP and image modeling.
Latent diffusion models are booming for video generation from text.
Can be applied to any modality with some structured latent space, but not SOTA for all modalities (e.g. not (yet?) competitive for text generation).

Parting Thoughts

Flow Matching: New kid on the block. "Stable Diffusion 3" id based on it.

Scaling Rectified Flow Transformers for High-Resolution Image Synthesis