Fairness in AI
CSE 849: Deep Learning
Vishnu Boddeti
Progress In Machine Learning
Speech Processing
Image Analysis
Natural Language Processing
Physical Sciences
State-of-Affairs
(report from the real-world)
May 23, 2016


Feb. 09, 2018


- Boulamwini and Gebru, "Gender Shades:Intersectional Accuracy Disparities in Commercial Gender Classification," FAT 2018

July 04, 2023


October 10, 2023
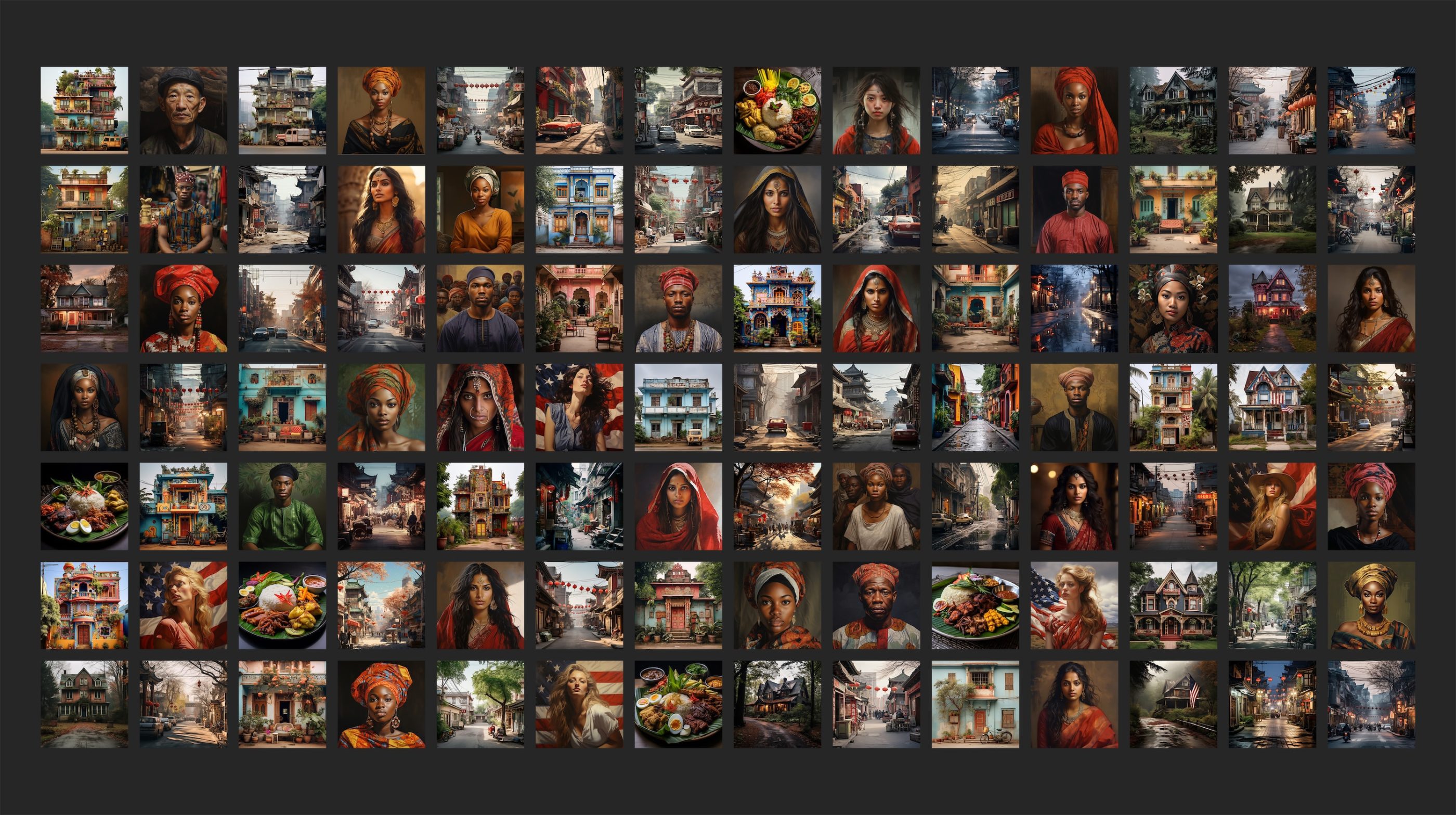


Economic Bias

- DeVries "Does Object Recognition Work for Everyone?," CVPRW 2020
Goal
Build ML systems that are fair while retaining utility.
Trade-Offs in Fair Machine Learning
Questions of Interest
- What are the trade-offs between fairness and utility?
- When do the trade-offs between fairness and utility exist?
- How to explicitly characterize the utility-fairness trade-offs?
What are the Trade-Offs in Fair Machine Learning?







Data Space Trade-Off
$$
\begin{equation}
\inf_{f\in \mathcal H_X} \left\{(1-\lambda)\underbrace{\inf_{g_Y\in \mathcal H_Y }\mathbb E_{X,Y} \left[\mathcal L_Y\left (g_Y(f(X), Y \right)\right]}_{Loss} + \lambda \underbrace{Dep(f(X),S|Y=y)}_{Unfairness} \right\}\nonumber
\end{equation}
$$
Label Space Trade-Off
$$
\begin{equation}
\inf_{Z\in \mathcal{L}^2} \left\{(1-\lambda)\underbrace{\inf_{g_Y\in \mathcal H_Y }\mathbb E_{Y} \left[\mathcal L_Y\left (g_Y\left(Z\right), Y \right)\right]}_{Loss} + \lambda \underbrace{Dep(Z,S|Y=y)}_{Unfairness} \right\}\nonumber
\end{equation}
$$
- "On Characterizing the Trade-off in Invariant Representation Learning," TMLR 2022
- "Utility-Fairness Trade-offs and How to Find Them," CVPR 2024
Fairness: The Multi-Headed Hydra
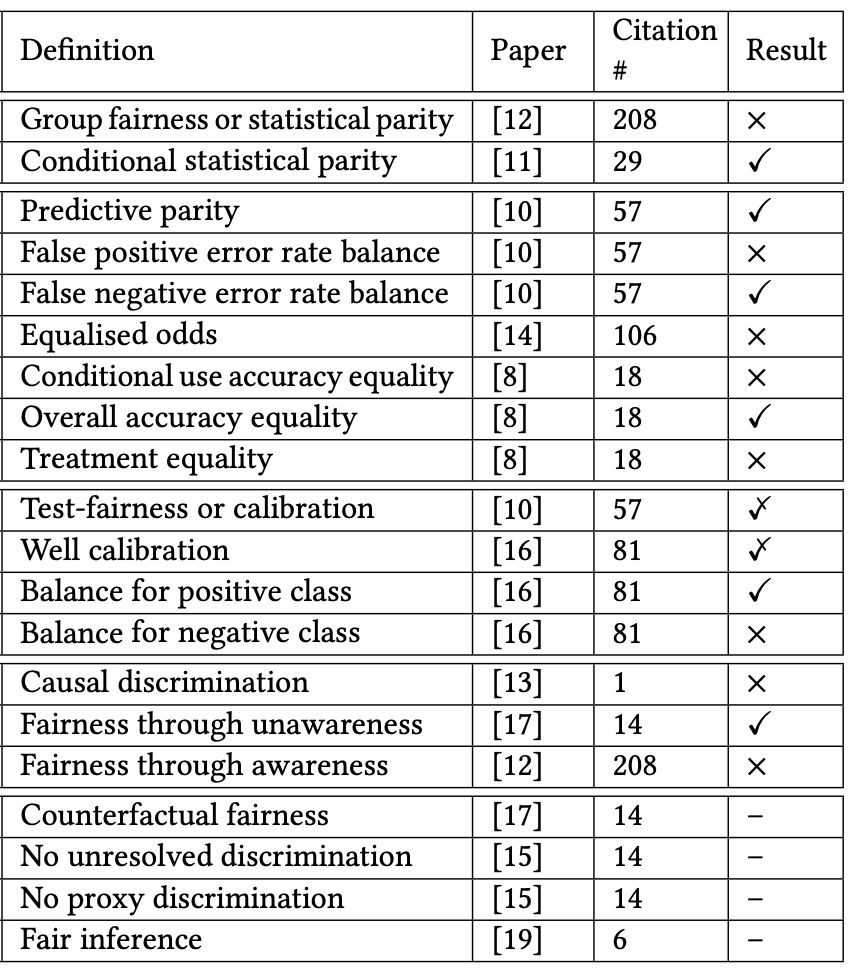
- Verma and Rubin, "Fairness Definitions Explained," International Workshop on Software Fairness, 2018
Fairness Definitions: Statistical Parity

- $P(\hat{Y}=1|S=1) = P(\hat{Y}=1|S=0)$
Probability of correct prediction is the same across demographic groups.
- $\hat{Y} \perp \!\!\! \perp S$
Fairness Definitions: Equalized Odds

- $P(\hat{Y}=y|Y=y, S=1) = P(\hat{Y}=y|Y=y, S=0)$
True positive rate of predictions is the same across demographic groups.
- $\hat{Y} \perp \!\!\! \perp S | Y$
Fairness Definitions: Equality of Opportunity

- $P(\hat{Y}=1|Y=1, S=1) = P(\hat{Y}=1|Y=1, S=0)$
Among eligible candidates, probability of correct prediction is the same across demographic groups.
- $\hat{Y} \perp \!\!\! \perp S | Y=1$
A Causal Perspective


A Subspace Geometry Perspective
- Case 1: when $\mathcal{S} \perp \!\!\! \perp \mathcal{T}$ (Gender, Age)


- Case 3: when $\mathcal{S} \sim \mathcal{T}$ ($\mathcal{T}\subseteq\mathcal{S}$)

- Case 2: when $\mathcal{S} \not\perp \!\!\! \perp \mathcal{T}$ (High Cheekbones, Gender)





- "Adversarial Representation Learning with Closed-Form Solutions," CVPRW 2020
From Fair Learning to Fair Representation Learning

$Z \perp \!\!\! \perp S \Rightarrow \hat{Y} \perp \!\!\! \perp S$
Learning Fair Representations
- Target Attribute: Smile & Demographic Attribute: Gender
- Problem Definition:
- Learn a representation $\mathbf{z} \in \mathbb{R}^d$ from data $\mathbf{x}$
- Retain information necessary to predict target attribute $\mathbf{t}\in\mathcal{T}$
- Remove information related to a desired demographic attribute $\mathbf{s}\in\mathcal{S}$



A Fork in the Road
- Design metric to measure sensitive demographic attribute information
- non-parameteric statistical dependence measures, this talk
- Learn metric to measure semantic attribute information
- probably feasible, many attempts
Game Theoretic Formulation



- Three player game between:
- Encoder extracts features $\mathbf{z}$
- Target Predictor for desired task from features $\mathbf{z}$
- Adversary extracts sensitive information from features $\mathbf{z}$
- Adversary: learned measure of semantic attribute information
How do we learn model parameters?




- Simultaneous/Alternating Stochastic Gradient Descent
- Update target while keeping encoder and adversary frozen.
- Update adversary while keeping encoder and target frozen.
- Update encoder while keeping target and adversary frozen.
ARL is Suboptimal
Unstable Optimization
Lack of Invariance Guarantees
Overview of FRL Solutions






- Standard Adversarial Representation Learning
- Linear Adversarial Measure: linear dependency between $Z$ and $S$ [ICCV 2019, CVPRW 2020]
- Non-Linear Adversarial Measure: Beyond linear dependency between $Z$ and $S$, but not all types [ECML 2021]
- Universal Dependence Measure: All types of dependency between $Z$ and $S$ [TMLR 2022]
- End-to-End Universal Dependence Measure: All types of dependency between $Z$ and $S$ [CVPR 2024].
Covariance Operator and Dependence Measure

Linear Dependence: $ C_{SZ}\approx \frac{1}{n}\tilde{\mathbf S} \tilde{\mathbf Z}^T$
Universal Dependence: $\Sigma_{SZ}\approx\frac{1}{n}\tilde{\mathbf K}_S\tilde{\mathbf K}_Z$
$\mathcal H_Z\times\mathcal H_S\rightarrow \mathbb R:\ Cov\left(\alpha(Z),\ \beta(S)\right)$ $=\big\langle \beta, \Sigma_{SZ}\, \alpha \big\rangle_{\mathcal H_S}, \Sigma_{SZ}:\mathcal H_Z\rightarrow \mathcal H_S$ $Z \perp \!\!\! \perp S \Leftrightarrow \Sigma_{SZ} =0 \Leftrightarrow \left\|\Sigma_{SZ}\right\| =0$, where $\|\cdot\|$ can be any operator norm HSIC$(Z,S)=\left\|\Sigma_{SZ}\right\|^2_{\text{HS}}=\displaystyle\sum_{\alpha\in\mathcal U_Z}\sum_{\beta\in \mathcal H_S}Cov^2(\alpha(Z),\beta(S))$Universal Dependence Measure

$\mathcal A_r:=\Big\{(f_1,\cdots,f_r)\,|\,Cov(f_i(X), f_j(X))+\gamma \langle f_i, f_j\rangle_{\mathcal H_X}=\delta_{i,j} \Big\}$
$\displaystyle\sup_{\mathbf f\in\mathcal A_r} {\Big\{J(\mathbf f):=(1-\lambda)\,\text{Dep}(Z, Y)}-\lambda\,\text{Dep}(Z, S)\Big\}$
Solution: eigenfunctions corresponding to the $r$ largest eigenvalues of $\big((1-\lambda)\, \Sigma_{YX}^*\,\Sigma_{YX}-\lambda\,\Sigma_{SX}^*\Sigma_{SX}\big)\mathbf f = \tau (\Sigma_{XX}+\gamma I)\mathbf f$
- "On Characterizing the Trade-off in Invariant Representation Learning," TMLR 2022
End-to-End Dependence Universal Measure

- Learning through alternating optimization
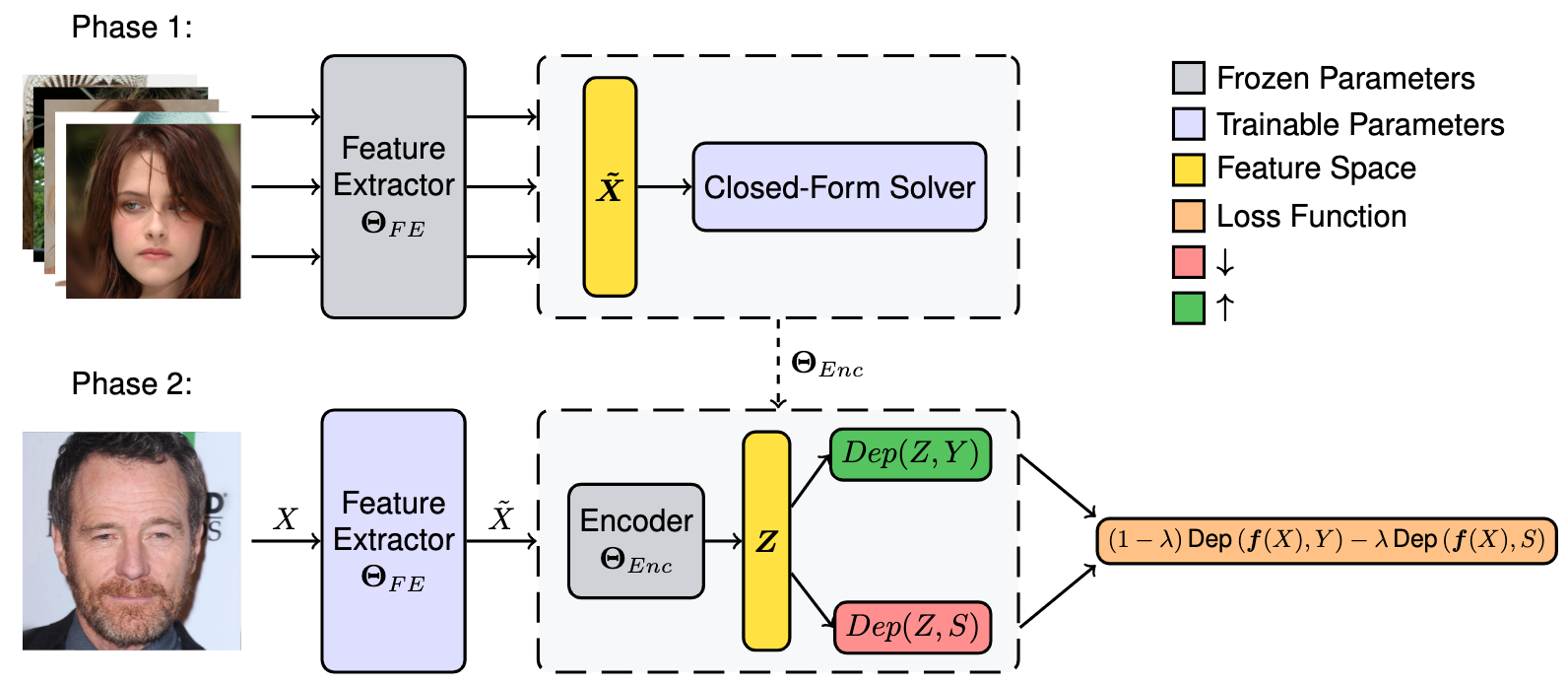
- "Utility-Fairness Trade-offs and How to Find Them," CVPR 2024
Estimating Trade-Offs on Real Datasets
Face Image Dataset

- Liu, Luo, Wang and Tang "Deep Learning Face Attributes in the Wild," ICCV 2015
CelebA Faces
- $Y$: high cheekbones (binary) and $S$: age and sex (continuous + binary)










- "On Characterizing the Trade-off in Invariant Representation Learning," TMLR 2022
- "Utility-Fairness Trade-offs and How to Find Them," CVPR 2024
Folktables
- $Y$: employement status (binary) and $S$: age (continuous)








- "On Characterizing the Trade-off in Invariant Representation Learning," TMLR 2022
- "Utility-Fairness Trade-offs and How to Find Them," CVPR 2024
Other Aspects of Fairness in AI
How about zero-shot models?


Fairness of Zero-Shot Predictions
- $Y$: high cheekbones (binary)
- $S$: sex (binary)


- "FairerCLIP: Debiasing CLIP's Zero-Shot Predictions using Functions in RKHSs," ICLR 2024
FairFace

- "FairerCLIP: Debiasing CLIP's Zero-Shot Predictions using Functions in RKHSs," ICLR 2024
Chicago Face Dataset
- $Y$: attractiveness (binary)
- $S$: gender (binary)

- "FairerCLIP: Debiasing CLIP's Zero-Shot Predictions using Functions in RKHSs," ICLR 2024
How about Data?


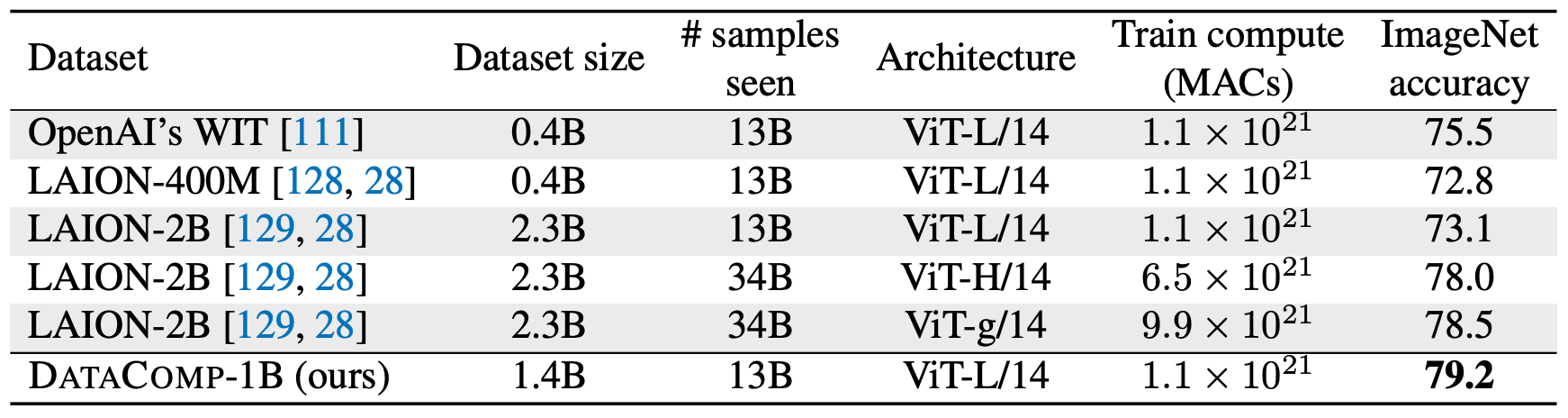
- DataComp: In search of the next generation of multimodal datasets, NeurIPS D&B 2023
Troubling Trends in Dataset Scaling
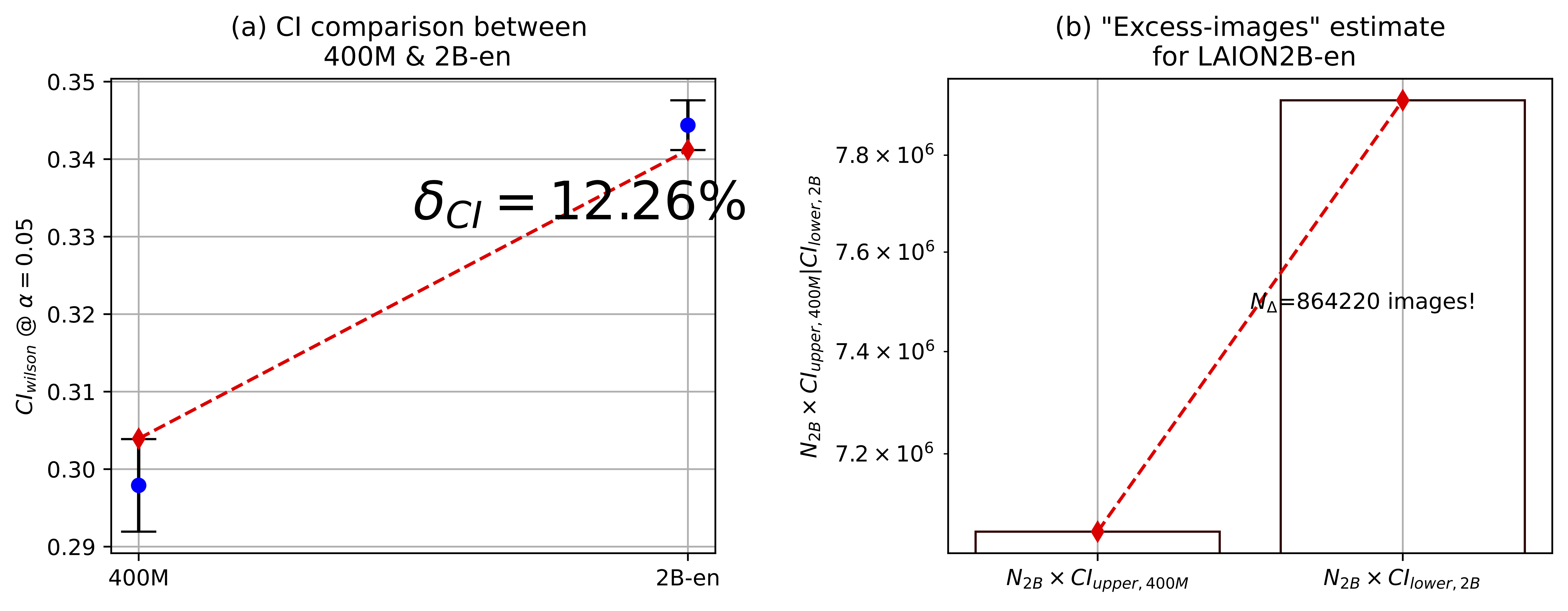
Scale exacerbates hate content.
- "On Hate Scaling Laws For Data-Swamps," arXiv:2306.13141
- "Into the LAION's Den: Investigating Hate in Multimodal Datasets," NeurIPS D&B Track 2023
Troubling Trends in Dataset Scaling
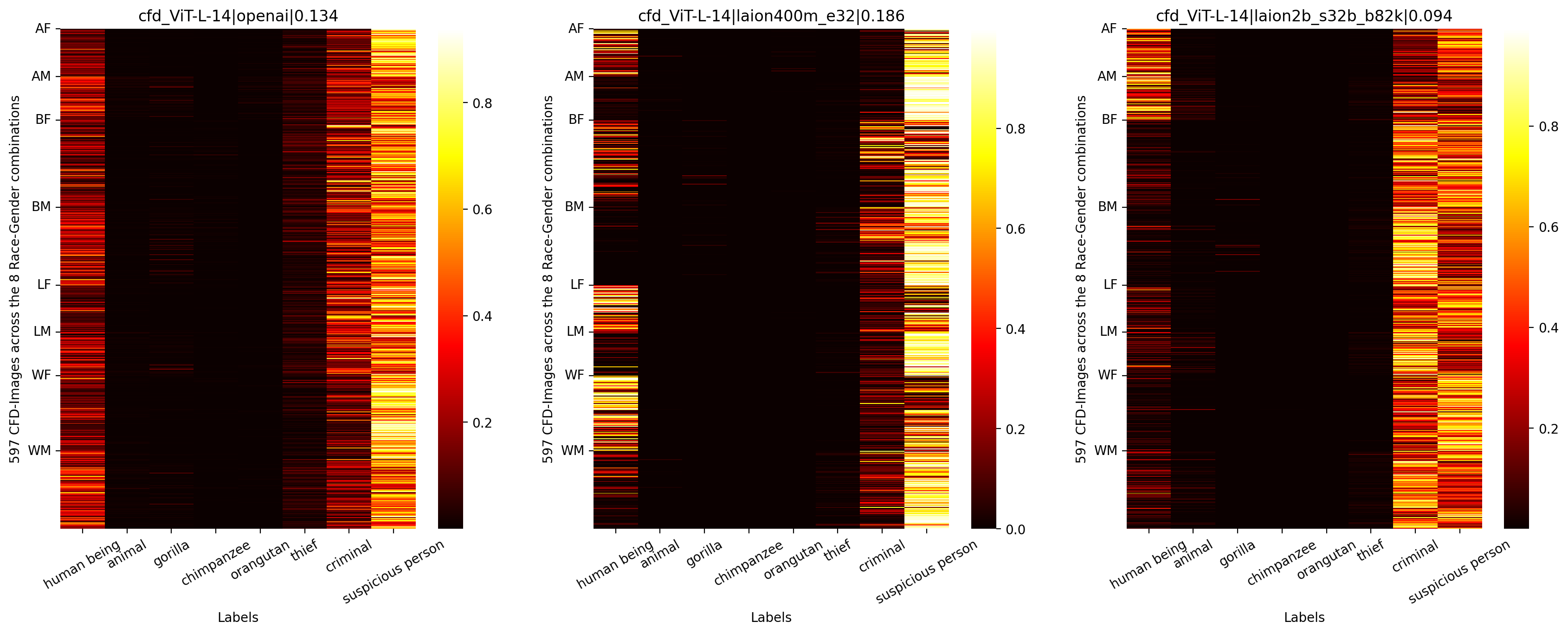
Scale exacerbates stereotypes.
- "On Hate Scaling Laws For Data-Swamps," arXiv:2306.13141
- "Into the LAION's Den: Investigating Hate in Multimodal Datasets," NeurIPS D&B Track 2023
Concluding Remarks
Summary
- Next generation of machine learning systems have to be designed with fairness constraints.
- Identified two trade-offs between utility and fairness.
- Proposed algorithms to characterize the utility-fairness trade-off.
- Appreciable gap exists between current solutions and ideal trade-off.