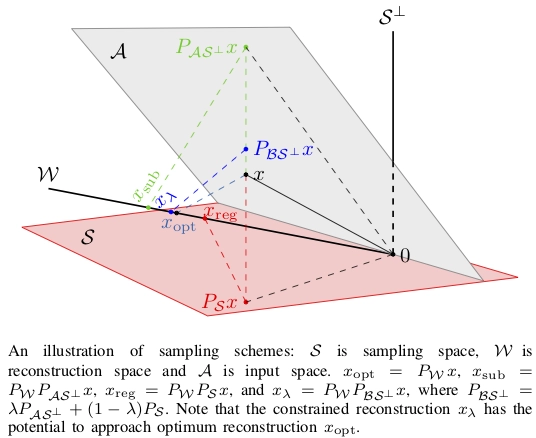
Abstract

This paper considers the problem of optimum reconstruction in generalized sampling-reconstruction processes (GSRPs). We propose constrained GSRP, a novel framework that minimizes the reconstruction error for inputs in a subspace, subject to a constraint on the maximum regret-error for any other signal in the entire signal space. This framework addresses the primary limitation of existing GSRPs (consistent, subspace and minimax regret), namely, the assumption that the a priori subspace is either fully known or fully ignored. We formulate constrained GSRP as a constrained optimization problem, the solution to which turns out to be a convex combination of the subspace and the minimax regret samplings. Detailed theoretical analysis on the reconstruction error shows that constrained sampling achieves a reconstruction that is 1) (sub)optimal for signals in the input subspace, 2) robust for signals around the input subspace, and 3) reasonably bounded for any other signals with a simple choice of the constraint parameter. Experimental results on sampling-reconstruction of a Gaussian input and a speech signal demonstrate the effectiveness of the proposed scheme.