Abstract

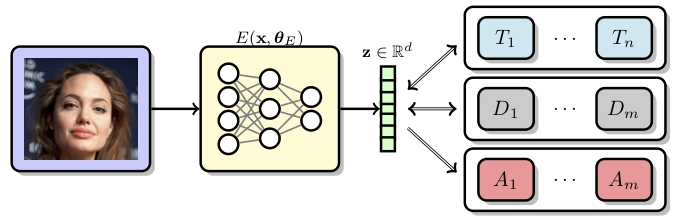
Image recognition systems have demonstrated tremendous progress over the past few decades thanks, in part, to our ability to learn a compact and robust representation of images. As we witness the wide spread adoption of these systems, it is imperative to consider the problem of unintended leakage of information from an image representation that might compromise the privacy of the data owner. This paper investigates the problem of learning an image representation that minimizes leakage of user information. We formulate the problem as an adversarial non-zero sum game of finding a good embedding function with two competing goals: to retain as much task dependent discriminative image information as possible, while simultaneously minimizing the amount of information, as measured by entropy, about other sensitive attributes of the user. We analyze the stability and convergence dynamics of the proposed formulation using tools from non-linear systems theory and compare to that of the corresponding adversarial zero-sum game formulation that optimizes likelihood as a measure of information content. Numerical experiments on UCI, Extended Yale B and CIFAR-10 datasets indicate that our proposed approach is able to learn image representations that exhibit high task performance while mitigating leakage of predefined sensitive information.

Poster