Source code
github.com/
Contributors
Latest commits

Abstract

Face recognition is a widely used technology with numerous large-scale applications, such as surveillance, social media and law enforcement. There has been tremendous progress in face recognition accuracy over the past few decades, much of which can be attributed to deep learning based approaches during the last five years. Indeed, automated face recognition systems are now believed to surpass human performance in some scenarios. Despite this progress, many crucial question still remains unanswered:

alt text

  • Given a face representation, how many identities can it resolve? In other words, what is the capacity of the face representation?
  • What is the minimal number of degrees of freedom or intrinsic dimensionality of a given face representation?
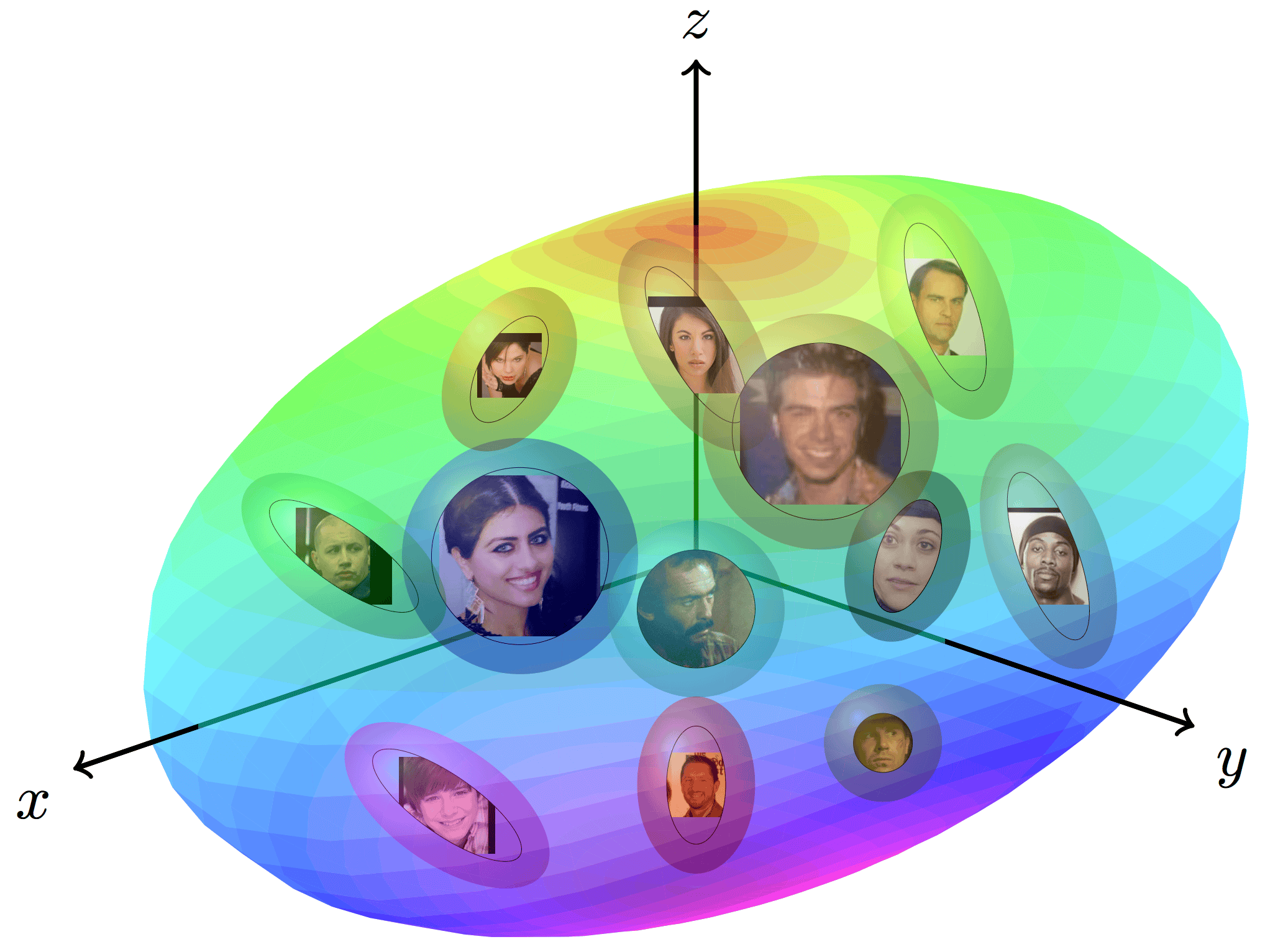
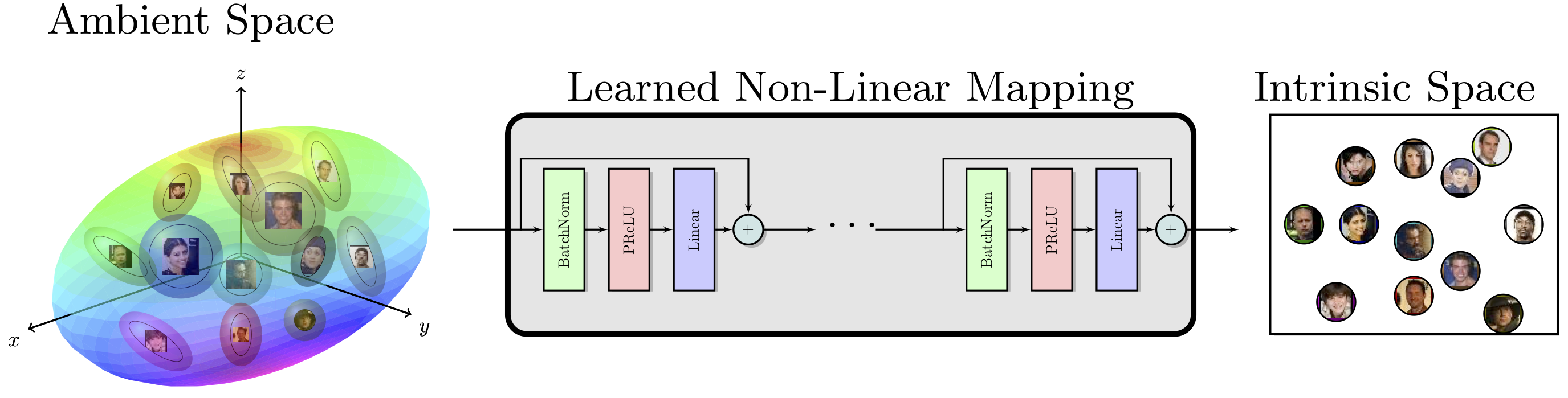
  • Can we find a mapping from the ambient representation to this minimal intrinsic space that retains it’s full utility? A scientific basis for addressing these questions will provide a better understanding of the merits and limitations of current face representations. We devise tools to information theoretically quantify and understand the content of a given representation. This involves modeling image representations that typically lie on complex entangled manifolds. Quantifying the size and shape of this manifold can enable us to directly estimate (1) an upper bound on the capacity of the representation, and (2) directly guage the information content of the representation manifold.

alt text

Contributions

  • Propose an information theoretic approach to estimate the capacity of a given face representation under the setting of a Gaussian Noise Channel.
  • Our capacity estimation model yields a capacity upper bound of \(1\times 10^{12}\) for the FaceNet representation at a false acceptance rate (FAR) of \(5\%\). (* Capacity reduces drastically as you lower the desired FAR with an estimate of \(2\times10^7\) and \(6\times10^3\) at FAR of \(0.1\%\) and \(0.001\%\), respectively.
  • Our results indicate that the performance of the FaceNet representation is significantly below the theoretical limit.
  • Propose an approach to estimate the intrinsic dimensionality of face representation. Facenet’s 128-d representation has an intrinsic dimensionality in the range of 9-12.
  • Demonstrate that a deep neural network based mapping can be learned to transform the ambient representation to the intrinsic representation while maintaining significant utility of the representation.

References