Source code
github.com/
Contributors
Latest commits

Abstract

In this project, we explore efficient convolutional neural network architectures for image analysis tasks. First we proposed local binary convolutional neural networks (LBCNN), which is motivated by local binary patterns (LBPs). LBCNN replaces dense real-valued learnable filters in CNN by pre-defined sparse local binary filters which do not need to be updated during the training process. LBCNN instead learns linear combination weights to combine the responses of the sparse binary filters. Building upon this we developed Perturbative Neural Networks (PNN) that explores an extreme version of LBCNN by making the convolutional weights one-sparse at the center i.e., no convolution. Both of these models are statistically and computationally more efficient than standard convolutional layers. Statisticall they are less prone to overfitting due to much lower model complexity. Computationally the enjoy significant savings in the number of parameters needed to be learned compared to CNN. But more importantly we seek to revisit the form and structure of standard convolutional layers that have been the workhorse of state-of-the-art visual recognition models. Empirically, these models, LBCNN and PNN, perform comparably with standard CNNs on a range of visual datasets (MNIST, CIFAR-10, PASCAL VOC, and ImageNet) with fewer parameters. ***

Overview

lbp alt text

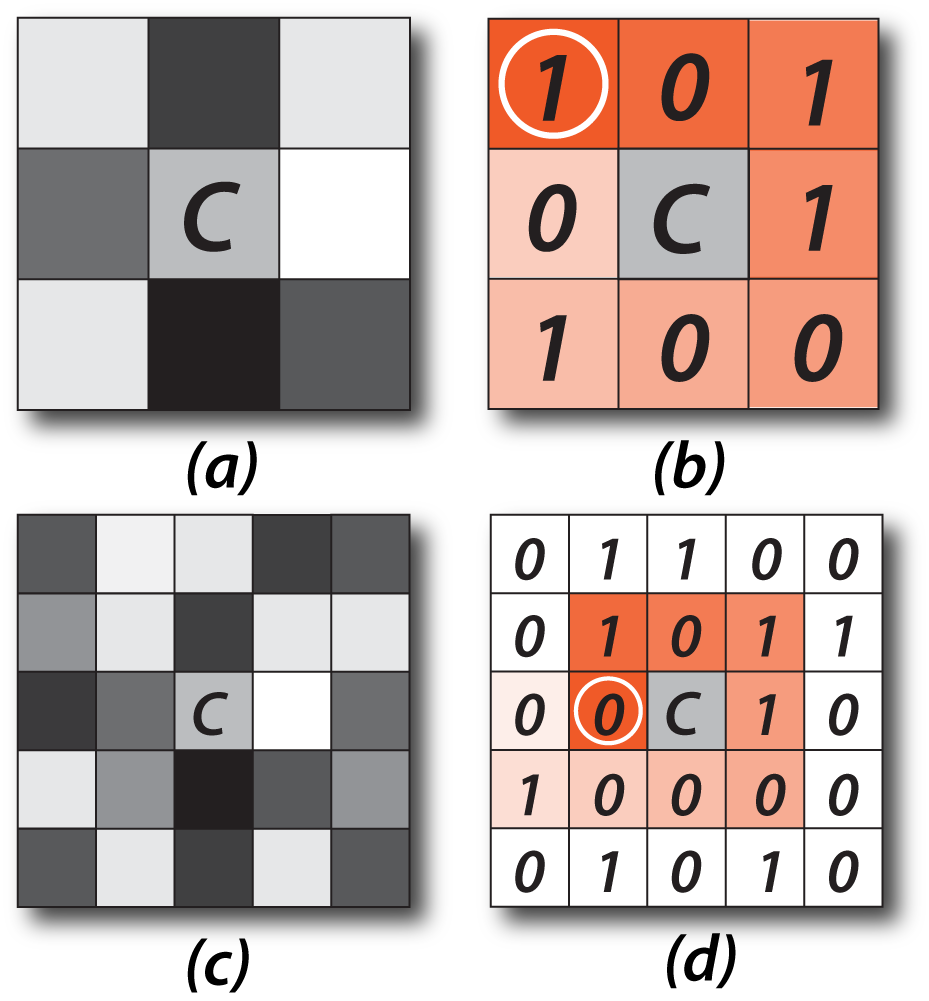
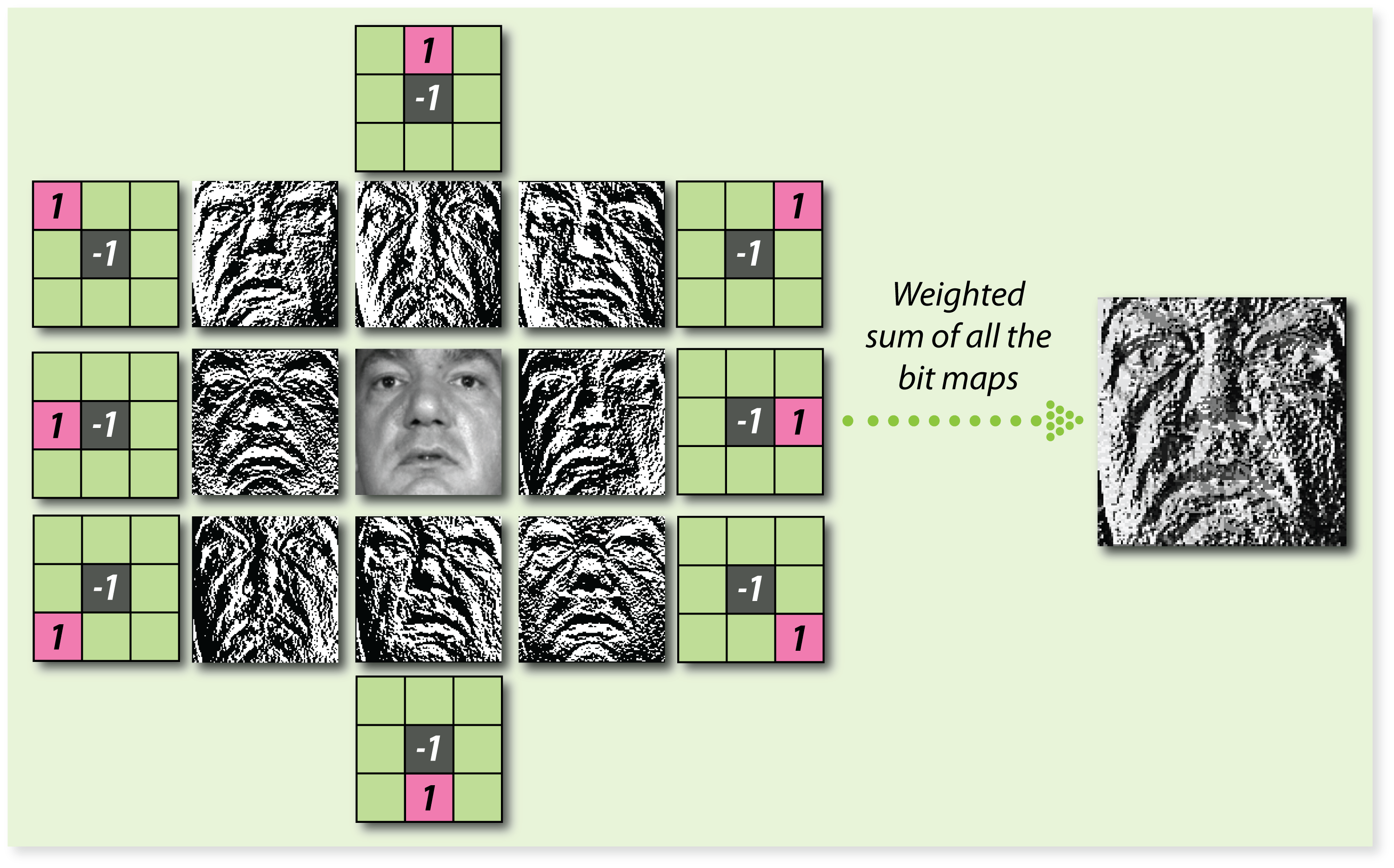
We draw inspiration from local binary patterns that have been very successfully used for facial analysis.

lbcnn

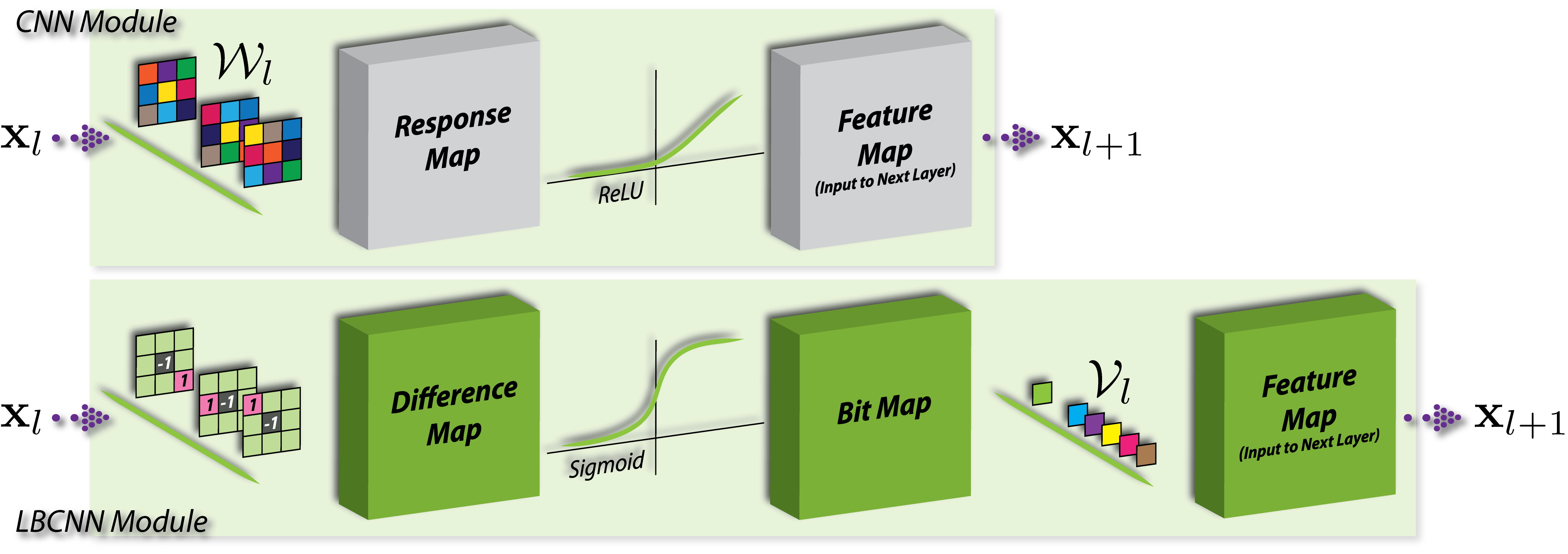
Our LBCNN module is designed to approximate a fully learnable dense CNN module.

sparsity alt text alt text

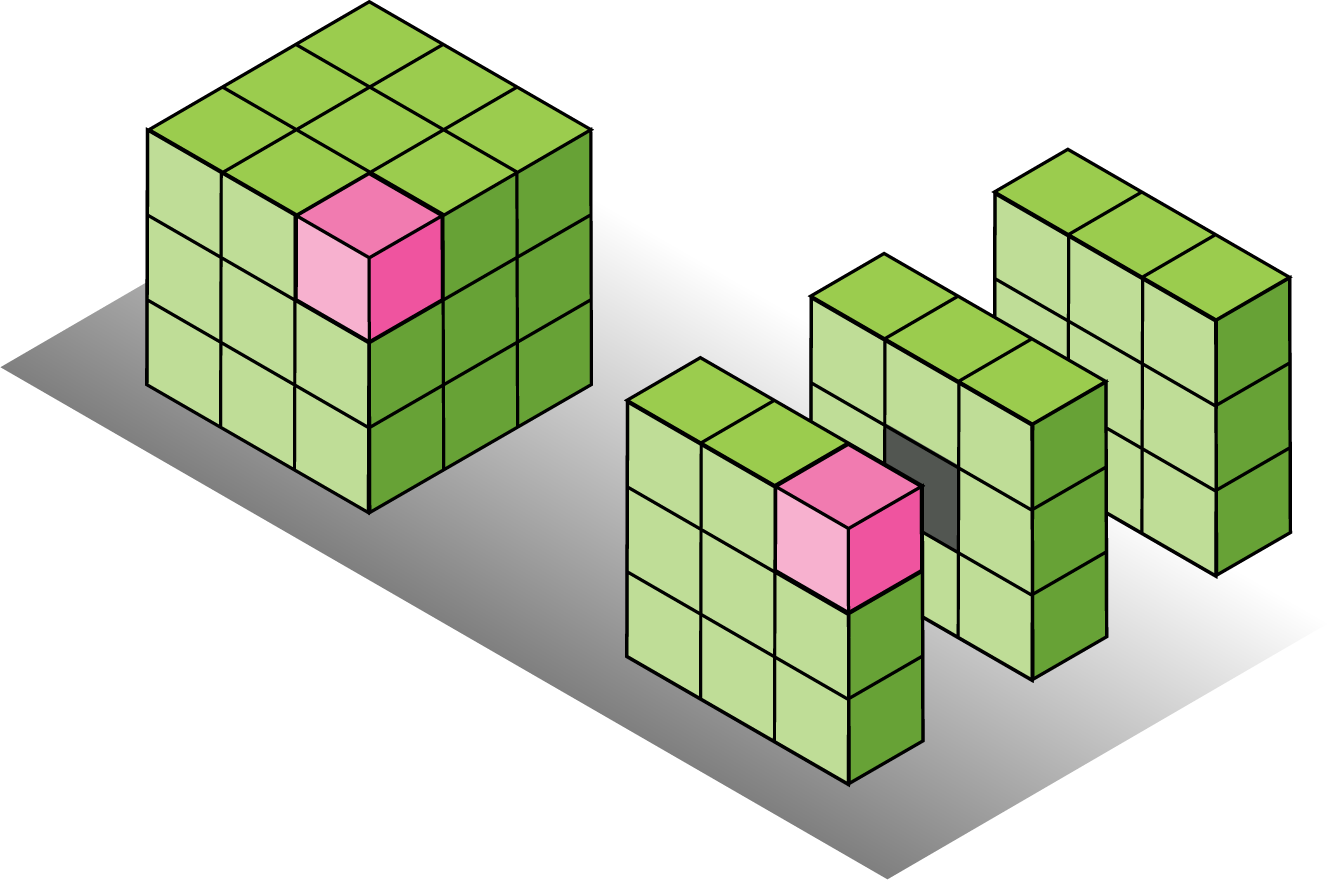
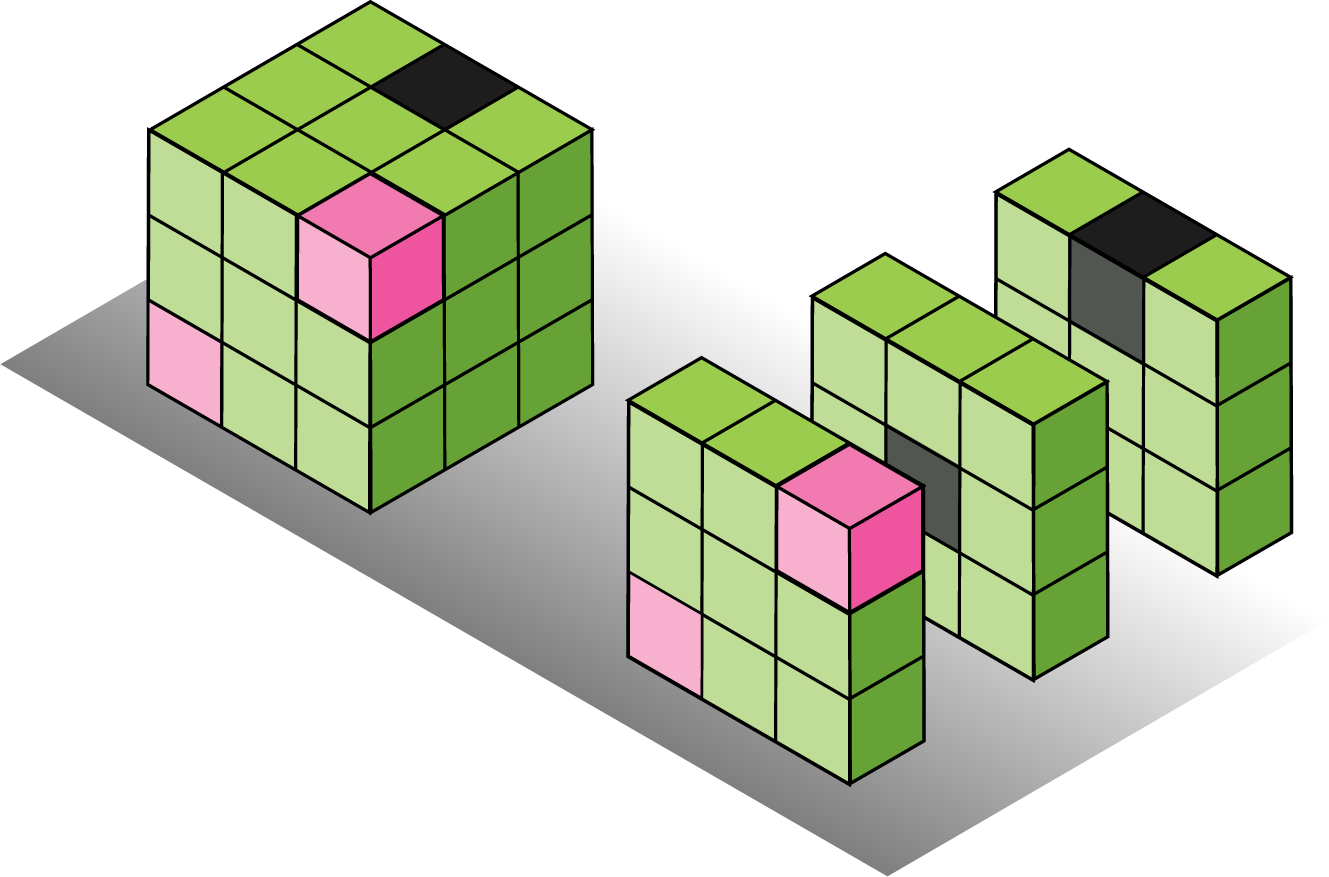
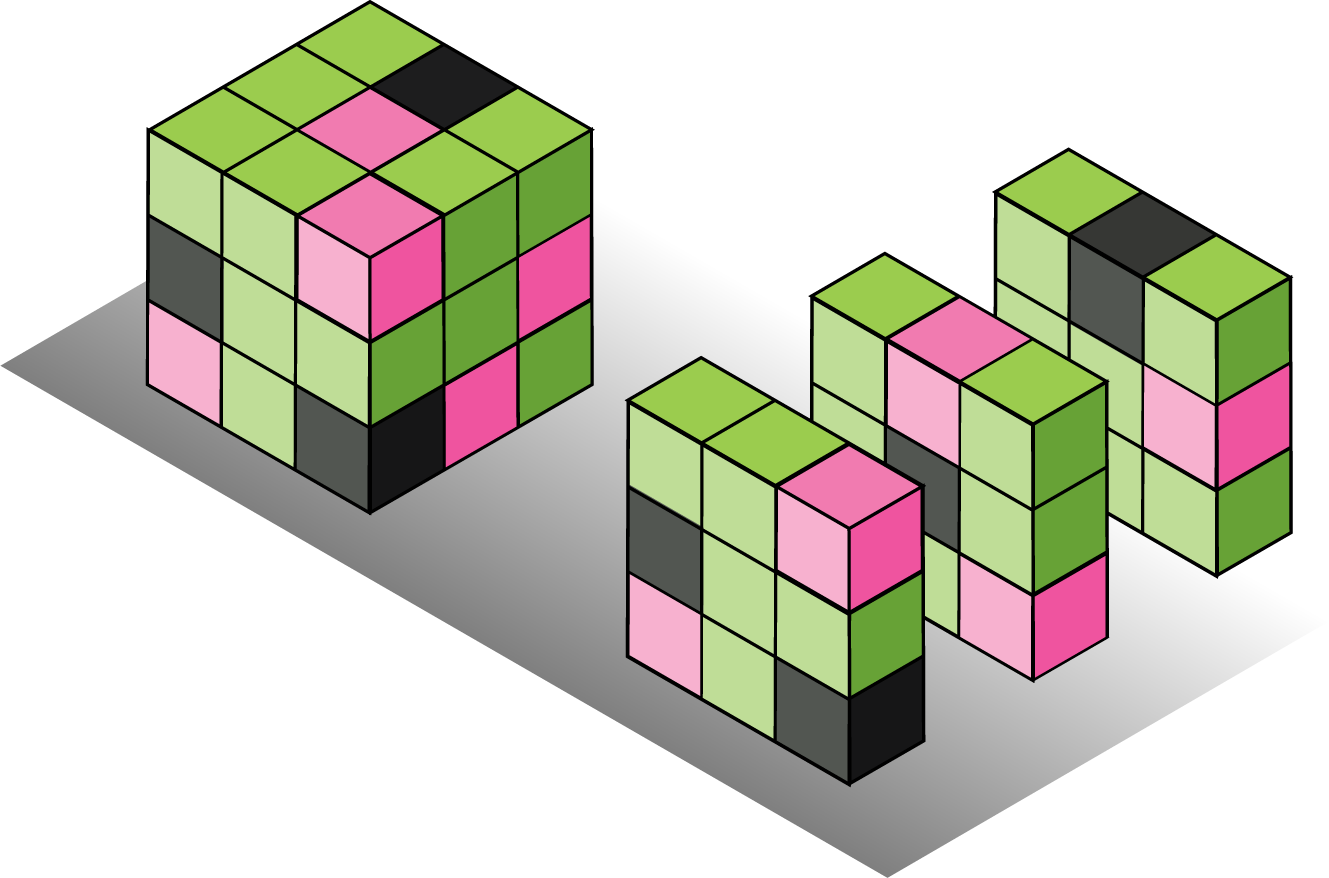
Binary Convolutional Kernels with different sparisty levels.

theorem

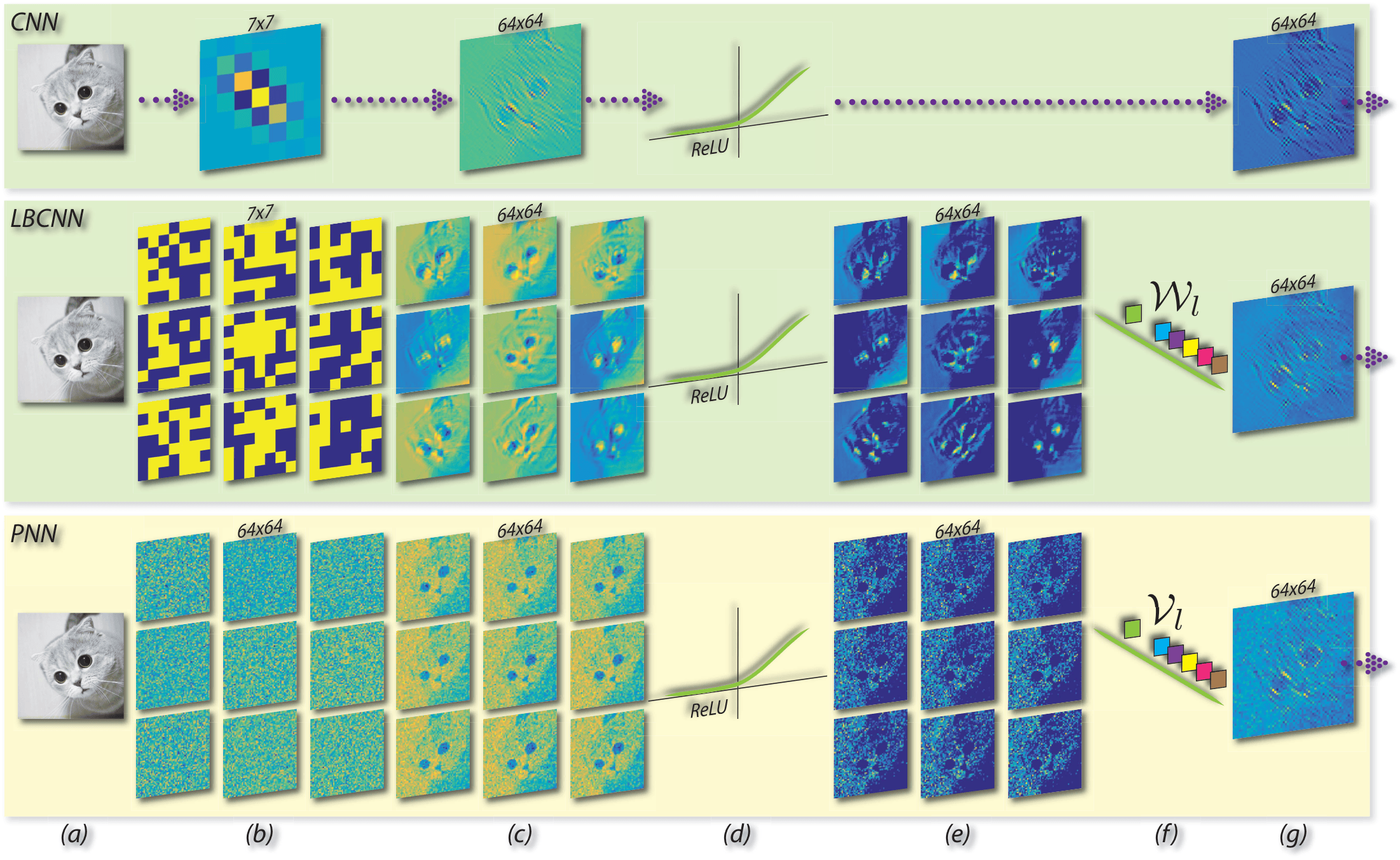
Perturbative Neural Networks as the evolution of the LBCNN architecture.

pnn

Contributions

  • Convolutional kernels inspired by local binary patterns.
  • Convolutional Neural Network architecture with fixed randomized sparse binary convolutional kernels.
  • Lightweight CNN with massive computational and memory savings.
  • Deep Neural Networks with an extreme version of sparse convolutional filters, no convolution.

References